itgle.com

某打字员一分钟内打错字的个数X是一个随机变量，服从λ=0.5的泊松分布，该打字员一分钟内未打错一个字的概率是（ ）。 A. 0.2231 B. 0.3679 C. 0. 4493 D. 0.6065

题目
某打字员一分钟内打错字的个数X是一个随机变量，服从λ=0.5的泊松分布，该打字员一分钟内未打错一个字的概率是（ ）。
A. 0.2231 B. 0.3679 C. 0. 4493 D. 0.6065

相似考题

1.可用泊松分布描述的随机变量的概率分布是（ ）。A．在一定时间内，某操作系统发生的故障数B．一个铸件上的缺陷数C．一页书上的错字个数D．太阳从东面升起

2.随机变量X服从正态分布，其观测值落在距均值的距离为2倍标准差范围内的概率约为( )。A．0.32B．0.5C．0.68D．0.95

3.随机变量X和Y相互独立,分别服从参数为2和4的泊松分布,则E(X＋Y)2=()。

4.如果一个贷款组合中违约贷款的个数服从泊松分布，如果该贷款组合的违约概率是 5%，那么该贷款组合中有10笔贷款违约的概率是( )。A．0.01B．0.012C．0.018D．0.03

更多“某打字员一分钟内打错字的个数X是一个随机变量，服从λ=0.5的泊松分布，该打字员一分钟内未打错一个字的概率是（ ）。 ”相关问题

  • 第1题：

    随机变量X服从参数为λ的泊松分布,且D(X)=2,则P{X=1}=()。


    参考答案：2e-2

  • 第2题：

    某打字员一分钟内打错字的个数X是一个随机变量，服从λ=0.5的泊松分布，该打字员一分钟内未打错一个字的概率是( )。

    A．0.2231

    B．0.3679

    C．0.4493

    D．0.6065


    正确答案：D
    解析：由题可知，x～P(0.5)即P(X=k)=，因此打字员一分钟内未打错一个字的概率为：P(X=0)=e-0.5=0.6065。

  • 第3题：

    设随机变量X服从参数为2的泊松分布,令Y=4X-3,则E(Y)=_______,D(Y)=_______.


    答案：1、32
    解析：
    因为X～P(2)，所以E(X)=D(X)=2，于是E(Y)=4E(X)-3=5，D(Y)=16D(X)=32.

  • 第4题：

    设随机变量X与Y相互独立，X的概率分布为P{X=1}=P{X=-1}=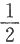，Y服从参数为λ的泊松分布.令Z=XY.
    　　(Ⅰ)求Cov(X，Z);
    　　(Ⅱ)求Z的概率分布.


    答案：
    解析：

  • 第5题：

    设随机变量X服从正态分布N（1，2），Y服从泊松分布P（2）。求期望E=（2X—y+3）。


    答案：
    解析：
    解：本题考查一些重要分布的数字特征与参数之间的关系。E（X）=1，E（y）=2 E（2X-y+3）=2E（X）-E（y）+3=3。

  • 第6题：

    设随机变量X服从参数为λ的泊松（Poisson）分布，且已知E[（X-1）（X-2）]=1＝1，则λ=（）。


    正确答案:1

  • 第7题：

    设随机变量X服从参数为3的泊松分布，则E（X-3）=（）


    正确答案:0

  • 第8题：

    设随机变量X服从泊松分布，若EX2=6，则P{X>1}=（）。


    正确答案:1-3e-2

  • 第9题：

    设X服从0—1分布，P=0.6，Y服从λ=2的泊松分布，且X，Y独立，则X+Y（）.

    • A、服从泊松分布
    • B、仍是离散型随机变量
    • C、为二维随机向量
    • D、取值为0的概率为0

    正确答案:B

  • 第10题：

    设随机变量X服从泊松分布，E（X）=6，证明：P{3


    正确答案:1/3

  • 第11题：

    单选题
    据统计某打字员每页的平均差错数为2个，假定差错的出现是随机的。现从该打字员打印的文件任抽一页文件，发现有3个错字。间：该打字员每页打字差错数的标准差是多少？（）
    A

    2

    B

    根号2（泊松分布）

    C

    3

    D

    根号3


    正确答案： B
    解析： 暂无解析

  • 第12题：

    填空题
    设随机变量X服从参数为λ的泊松分布，且已知E[（X-1）（X-2）]=1，则λ=____.

    正确答案： 1
    解析：
    E[（X-1）（X-2）]=E（X2）-3E（X）+2=D（X）+E2（X）-3E（X）+2
    =λ+λ2-3λ+2=1
    解得λ=1

  • 第13题：

    随机变量X服从参数为的λ泊松分布,则X的分布列为();若E(X－1)(X－2)=1,则λ=()。


    参考答案：

  • 第14题：

    某打字员一分钟内打错字的个数X是一个随机变量，服从A = 0. 5的泊松分布，该打字员一分钟内未打错一个字的概率是（ ）。

    A. 0.2231 B. 0.367 9
    C. 0. 449 3 D. 0. 606 5


    答案：B
    解析：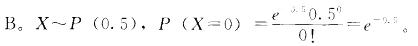

  • 第15题：

    设随机变量X服从参数为λ的泊松分布,且P（X=O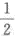）=P（X=1）,则P(X≥1)=_______.


    答案：
    解析：

  • 第16题：

    一个随机变量若服从标准正态分布，则它的取值点位于(0，+∞)内的概率为()

    A.0
    B.0.5
    C.1
    D.+∞

    答案：B
    解析：
    推断统计；推断统计的数学基础；正态分布。 平均数为0且标准差为1的正态分布就是标准正态分布。标准正态分布的对称轴为x=o，正态分布曲线下的面积为1，故从(o，+ ∞ )对应的曲线下面积为0.5，即为对应的概率。

  • 第17题：

    一铸件上的缺陷数X服从泊松分布，每铸件上的平均缺陷数是0.5，则：一铸件上仅有一个缺陷的概率为（）。

    • A、0.535
    • B、0.303
    • C、0.380
    • D、0.335

    正确答案:B

  • 第18题：

    设随机变量X服从参数λ=2的泊松分布，则P（X≥1）=（）


    正确答案:1-e-2

  • 第19题：

    设随机变量X服从参数为2的泊松分布，且Y=3X-2，则E（Y）=（）。


    正确答案:4

  • 第20题：

    对随机变量X来说，如果EX≠DX，则可断定X不服从（）。

    • A、二项分布
    • B、指数分布
    • C、正态分布
    • D、泊松分布

    正确答案:D

  • 第21题：

    对于随机变量X服从泊松分布，即X~p（0.05），则E（X）=（）

    • A、0.05
    • B、20
    • C、0.0025
    • D、0.5

    正确答案:A

  • 第22题：

    设随机变量X，Y相互独立，其中X在[0，6]上服从均匀分布，Y服从参数为λ=3的泊松分布，记Z=X-2Y，则D（Z）=（）。


    正确答案:15

  • 第23题：

    填空题
    设随机变量X服从参数为1的泊松分布，则P{X＝E（X2）}＝____。

    正确答案： 1/(2e)
    解析：
    因为X服从参数为1的泊松分布，故E（X）＝D（X）＝1，E（X2）＝D（X）＋（E（X））2＝1＋1＝2，故P{X＝2}＝12e－1/2!＝1/（2e）。

相关内容