itgle.com

关于正态分布N(μ，ó2。)的参数口的说法，正确的有（ ）。A.μ表示分布均值B.μ是分布的对称中心C.在μ附近取值的机会小D.在μ附近取值的机会大E.μ表示分布的散布大小

题目

关于正态分布N(μ，ó2。)的参数口的说法，正确的有（ ）。

A.μ表示分布均值

B.μ是分布的对称中心

C.在μ附近取值的机会小

D.在μ附近取值的机会大

E.μ表示分布的散布大小

相似考题

1.下列关于“右偏分布”的表述错误的是( )。A．右偏分布是正态分布的形式之一B．符合右偏分布的随机变量大量取值在左边，少量分布在右边C．符合右偏分布的随机变量少量取值在左边，大量分布在右边D．随机变量的分布很散

2.下列关于“右偏分布”的描述错误的是（ ）。 A．右偏分布是正态分布的形式之一 B．符合右偏分布的随机变量大量取值在左边，少量分布在右边 C．符合右偏分布的随机变量少量取值在左边，大量分布在右边 D．随机变量的分布很散A.缩小公差B.增大离散度C.减小偏离量D.以上都不正确

3.正态分布N(μ,σ2)中σ的含义及性质为________。A．正态分布的标准差B．分布的分散程度C．在σ附近取值机会小D．在σ附近取值机会大

4.关于中心极限定理，下列说法正确的是( )。A．多个随机变量的平均值(仍然是一个随机变量)服从或近似服从正态分布B．几个相互独立同分布随机变量，其共同分布不为正态分布或未知，但其均值μ和方差σ2都存在，则在n相当大的情况下，样本均值X近似服从正态分布N(μ，σ2/n)C．无论什么分布(离散分布或连续分布，正态分布或非正态分布)，其样本均值X的分布总近似于正态分布D．设n个分布一样的随机变量，假如其共同分布为正态分布N(μ，σ2)，则样本均值X仍为正态分布，其均值不变仍为μ，方差为σ2/n

更多“关于正态分布N(μ，ó2。)的参数口的说法，正确的有（ ）。A.μ表示分布均值B.μ是分布的对称中心C.在μ附近取值的机会小D.在μ附近取值的机会大E.μ表示分布的散布大小”相关问题

  • 第1题：

    某水文变量的离势系数Cv值大，表示该水文变量()。

    A.会以较小的概率分布在均值附近

    B.会以较大的概率分布在均值附近

    C.为正偏

    D.概率密度函数曲线较为尖瘦


    参考答案：A

  • 第2题：

    关于正态分布曲线的特点说法有误的是()。

    A、正态分布以均值μ为中心，左右对称。曲线下面积集中在中心部分，越远离中心。曲线越接近横轴

    B、正态分布中的X取值范围理论上没有边界(-∞<X<∞)，X越远离μ。函数值f(X)越接近，但不会等于0

    C、正态分布曲线由2个参数μ和σ决定。是变异参数，决定分布曲线的形态，σ是位置(即平均水平)参数，决定分布曲线在横轴的偏移位置

    D、正态分布曲线下的面积分布有一定的规律。所有正态分布曲线，在μ左右的任意个标准差范围内面积相同


    答案：C

  • 第3题：

    关于正态分布描述正确的是（ ）。

    A.正态分布是质量管理中最重要也是最常用的分布

    B.正态分布有两个参数μ与σ2,其中μ为均值，σ2是正态分布的公差

    C.σ是正态分布的标准差，σ愈小，分布愈分散，σ愈大，分布愈集中

    D.标准差σ不变时，不同的均值对应的正态曲线的形状完全相同

    E.均值μ不变时，不同的标准差对应的正态曲线的形状不同


    正确答案：ADE

  • 第4题：

    关于中心极限定理，下列说法正确的是（ ）。
    A.多个随机变量的平均值（仍然是一个随机变量）服从或近似服从正态分布
    B. n个相互独立同分布随机变量，其共同分布不为正态分布或未知，但其均值μ和方差σ2都存在，则在n相当大的情况下，样本均值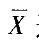
    近似服从正态分布N(μ, σ2/n)
    C.无论什么分布（离散分布或连续分布，正态分布或非正态分布），其样本均值的分布总近似于正态分布
    D.设n个分布一样的随机变量，假如其共同分布为正态分布N(μ, σ2)则样本均值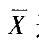仍为正态分布，其均值不变仍为μ，方差为 σ2/n


    答案：B
    解析：
    AC两项成立的前提条件是多个随机变量必须相互独立且同分布；D项要求这些随机变量相互独立。

  • 第5题：

    下列关于正态分布的描述正确的是（ ）。
    A.正态分布是质量管理中最重要也是最常用的分布
    B.正态分布有两个参数μ与σ2，其中μ为均值，σ2是正态分布的方差
    C. σ是正态分布的标准差，σ愈大，分布愈分散，σ愈小，分布愈集中
    D.标准差σ不变时，不同的均值对应的正态曲线的形状完全相同
    E.均值μ不变时，不同的标准差对应的正态曲线的位置不同


    答案：A,C,D
    解析：
    B项，正态分布的两个参数应分别是μ和σ，但表示时用σ2表示，记为N(μ，σ2)； E项，均值μ不变时，相同的标准差对应的正态曲线的位置相同，形状相同，当标准差不同时，形状也不同。

  • 第6题：

    下列对正态分布的说法中，正确的是（ ）。
    Ⅰ正态分布密度函数的显著特点是中间高两边低
    Ⅱ正态分布密度函数是一条光滑的钟形曲线
    Ⅲ正态分布距离均值越近的地方数值越集中，而在离均值较远的地方数值则很稀疏
    Ⅳ正态分布密度函数越“瘦”，正态分布集中在均值附近的程度越大

    A.Ⅰ、Ⅱ、Ⅲ
    B.Ⅰ、Ⅱ、Ⅳ
    C.Ⅱ、Ⅲ、Ⅳ
    D.Ⅰ、Ⅱ、Ⅲ、Ⅳ

    答案：D
    解析：
    正态分布密度函数的显著特点是中间高两边低正态分布密度函数是一条光滑的钟形曲线
    正态分布距离均值越近的地方数值越集中，而在离均值较远的地方数值则很稀疏
    正态分布密度函数越“瘦”，正态分布集中在均值附近的程度越大
    知识点：了解正态分布的特征；

  • 第7题：

    下列表述中正确的有( )。

    A.总体均值的置信区间都是由样本均值加减估计误差得到

    B.在小样本情况下，对总体均值的估计都是建立在总体服从正态分布的假定条件下

    C.当样本量n充分大时，样本均值的分布近似服从正态分布

    D.当总体服从正态分布时，无论样本量大小，样本均值一定服从正态分布

    E.对总体均值进行区间估计时，不需要考虑总体方差是否已知

    答案：A,B,D
    解析：
    选项C错误，若总体为未知的非正态总体，当样本量n充分大时，样本均值的分布近似服从正态分布；选项E错误，对总体均值进行区间估计时，需要考虑总体方差是否已知，当总体方差未知时，需要用样本方差来代替总体方差。

  • 第8题：

    关于正态分布N(μ,σ2)参数的说法，正确的有（ ）。

    A. σ2是方差 B. σ2越小，分布越集中
    c. σ表示分布的位置特征 D. σ2越大，分布越集中
    E.μ与σ2同量纲


    答案：A,B
    解析：

  • 第9题：

    关于正态分布函数，下列说法正确的是（ ）。
    A. σ越大，分布越集中；σ越小，分布越分散
    B.质量特性X在μ附近取值的机会不一定最大
    C.σ越大，分布越分散；σ越小，分布越集中
    D.μ不是正态分布的中心


    答案：C
    解析：
    在正态分布中，σ越大，分布越分散，σ越小，分布越集中；μ是正态分布的中心，质量特性X在μ附近取值的机会最大。

  • 第10题：

    关于正态分布的说法，正确的有（ ）。
    A.正态分布是质量管理中最重要也是最常用的分布
    B.正态分布有两个参数μ与σ，其中μ为均值，σ2是正态分布的方差
    C. σ是正态分布的标准差，σ愈大，分布愈分散；σ愈小，分布愈集中
    D.标准差σ不变时，不同的均值对应的正态曲线的形状完全相同
    E.均值μ不变时，不同的标准差对应的正态曲线的形状完全相同


    答案：A,B,C,D
    解析：

  • 第11题：

    关于正态分布的正确说法是（）。

    • A、正态分布的失效率λ等于常数。
    • B、正态分布具有对称性，它的主要参数是均值μ和方差σ2，记为N.μ，σ2）
    • C、均值μ决定正态分布曲线的位置，代表分部的中心倾向。
    • D、方差σ2决定正态分布曲线的形状，表征分布的离散程度。

    正确答案:B,C,D

  • 第12题：

    多选题
    正态分布N（μ,σ2）中σ的含义及性质为（　　）。
    A

    正态分布的标准差

    B

    分布的分散程度

    C

    在σ附近取值机会小

    D

    在σ附近取值机会大

    E

    σ愈大，分布愈分散；σ愈小，分布愈集中


    正确答案： D,B
    解析： 正态分布含有两个参数μ与σ，常记为N（μ，σ2）。其中μ为正态分布的均值，它是正态分布的中心，质量特性X在μ附近取值的机会最大。σ2是正态分布的方差，σ是正态分布的标准差。σ愈大，分布愈分散；σ愈小，分布愈集中。

  • 第13题：

    某水文变量的离势系数C，值大，表示该水文变量()。

    A.会以较小的概率分布在均值附近

    B.会以较大的概率分布在均值附近

    C.为正偏

    D.概率较大


    参考答案：A

  • 第14题：

    关于正态分布，错误的一项是

    A．标准正态分布的方差与标准差相同

    B．μ决定曲线的位置

    C．σ决定曲线的形状

    D．服从正态分布的变量在区间(μ- 3σ，μ+3σ)外取值的概率小于1%

    E．正态分布都可以通过变换化为标准正态分布


    正确答案：D
    (答案：D)服从正态分布的变量在区间μ±2.58σ外取值的概率就已经小于1%。

  • 第15题：

    关于正态分布N(μ,σ2)的说法，正确的有（ ）。

    A.μ是分布的对称中心

    B.在μ附近取值的机会小

    C.在μ附近取值的机会大

    D.σ 越小，分布越集中

    E.σ 越大，分布越集中


    答案：A,C,D
    解析：

  • 第16题：

    下列关于随机变量特征数的描述有误的有（ ）。A.均值用来表示分布的中心位置用E(X)表示
    B.方差用来表示分布的散布大小，用Var(X)表示
    C.标准差是方差的平方，实际中更常用标准差来表示分布的散布的大小
    D.离均值越近的值发生的可能性越大
    E.对于独立的随机变量，其方差和标准差具有可加性


    答案：C,D,E
    解析：
    C项，方差是标准差的平方；D项，事件发生的可能性大小需要根据具体的分布来确定；E项，在条件成立时只有方差具有可加性，而标准差不具有可加性。

  • 第17题：

    下列关于t分布的表述，错误的是()

    A.以均值为1左右对称分布
    B.随着乃的大小而变化的一簇曲线
    C.n>30时，接近正态分布
    D.变量取值在- ∞到+∞之间

    答案：A
    解析：
    推断统计；推断统计的数学基础。 f分布是均值为0、左右对称的单峰分布；分布的形状随样本容量n的变化而变化；当n>30时，接近正态分布；变量取值为-∞到+∞。

  • 第18题：

    从均值为μ，方差为σ2（有限）的任意一个总体中抽取样本容量为n的样本，下列说法正确的是( )。


    A.当n充分大时，样本均值图.png的分布近似服从正态分布

    B.只有当n <30时，样本均值图.png的分布近似服从正态分布

    C.样本均值图.png的分布与n无关

    D.无论n多大，样本均值图.png的分布都为非正态分布

    答案：A
    解析：
    根据中心极限定理，设从均值为μ，方差为σ2的任意一个总体中抽取样本量为 n的样本，当n充分大时，样本均值的抽样分布近似服从均值为μ，方差为σ2/n的正态分布。

  • 第19题：

    关于正态分布，错误的一项是

    A.标准正态分布的方差与标准差相同
    B.μ决定曲线的位置
    C.σ决定曲线的形状
    D.服从正态分布的变量在区间（μ－2σ，μ+2σ）外取值的概率小于1％
    E.正态分布都可以通过变换化为标准正态分布

    答案：D
    解析：
    D选项在区间外取值的概率应大于1%。因为是正态分布，其在区间内的取值概率为95%对应的值为1.96，在概率为99%对应的值为2.58。本题1.96＜2＜2.58，所以在区间内的取值为95%～99%，那么其在区间外的取值应该大于1%。

  • 第20题：

    正态分布N(μ,σ2)中σ的含义及性质为（ ）。
    A.正态分布的标准差 B.分布的分散程度
    C.在σ附近取值机会小 D.在σ附近取值机会大
    E. σ愈大，分布愈分散；σ愈小，分布愈集中


    答案：A,B,E
    解析：
    正态分布含有两个参数μ与σ，常记为N(μ，σ2)。其中μ为正态分布的均值, 它是正态分布的中心，质量特性X在μ附近取值的机会最大。σ2是正态分布的方差，σ是正态分布的标准差。σ愈大，分布愈分散；σ愈小，分布愈集中。

  • 第21题：

    关于正态分布N（μ，σ2)的参数μ的说法，正确的有（ ）。
    A. μ表示分布均值 B. μ是分布的对称中心
    C.在μ附近取值的机会小 D.在μ附近取值的机会大
    E.μ表示分布的散布大小


    答案：A,B,D
    解析：
    。表示分布散布大小的是σ而非μ

  • 第22题：

    正态分布N（μ2，σ2）中，参数μ的物理意义表示正态分布的（）。


    正确答案:均值

  • 第23题：

    单选题
    关于正态分布函数，下列说法正确的是（　　）。
    A

    σ越大，分布越集中；σ越小，分布越分散

    B

    质量特性X在μ附近取值的机会不一定最大

    C

    σ越大，分布越分散；σ越小，分布越集中

    D

    μ不是正态分布的中心


    正确答案： B
    解析： 在正态分布中，σ越大，分布越分散，σ越小，分布越集中；μ是正态分布的中心，质量特性X在μ附近取值的机会最大。

相关内容