itgle.com

在研究某一问题中使用F检验法，如果在显著性水平α=0.05的水平下，统计量F大于临界值F0.95(n1，n2)，则在α=0.01水平下，可能的结论有( )。A．F＞F0.99(n1，n2)B．F≤F0.99(n1，n2)C．F0.99(n1，n2)＞F0.95(n1，n2)D．F0.99(n1，n2)＜F0.95(n1，n2)E．F=F0.99(n1，n2)

题目

在研究某一问题中使用F检验法，如果在显著性水平α=0.05的水平下，统计量F大于临界值F0.95(n1，n2)，则在α=0.01水平下，可能的结论有( )。

A．F＞F0.99(n1，n2)

B．F≤F0.99(n1，n2)

C．F0.99(n1，n2)＞F0.95(n1，n2)

D．F0.99(n1，n2)＜F0.95(n1，n2)

E．F=F0.99(n1，n2)

相似考题

1.当a＝0.05时，用F检验法检验回归方程中x对y的影响是( )。A．显著B．不显著C．不能确定 附：F0.95(1，12)＝4.75；F0.975(1，12)＝6.55；F0.95(1，13)＝4.60

2.如果在显著性水平0.05时，查表得到的F的临界值是3.48，那么做方差分析的结论是( ) 。A．在显著性水平0.05上温度这一因子是显著的B．在显著性水平0.05上温度这一因子是不显著的C．在显著性水平0.05上不同温度下的平均得率有显著差异D．在显著性水平0.05上不同温度下的平均得率无显著差异

3.在比较三种加工方法(记为因子A)的试验中，已知三个水平下各进行了6次、5次、4次试验，作方差分析求得的因子的平方和为155.64，误差平方和为85.34，则有( )。A．F比为1.823B．F比为1.824C．F比为10.94D．若取显著性水平为0.05，那么当F＜F0.95(2，12)时因子是显著的E．若取显著性水平为0.05，那么当F＞F0.95(2，12)时因子是显著的

4.在研究指标y与某物质的含量x的线性回归方程时，收集了10组数据，求得回归平方和为 255.4，残差平方和为27.5，在显著性水平0.05时F的临界值为5.32，则结论是( )。A．F＝9.287B．F＝74.30C．在0.05水平上方程不显著D．在0.05水平上方程显著E．F＝9.287

参考答案和解析
正确答案：ABCE
解析：因为F0.99(n1，n2)＞F0.95，所以若F＞F0.95，则有可能F＞F0.99，也有可能F≤F0.99。
更多“在研究某一问题中使用F检验法,如果在显著性水平α=0.05的水平下,统计量F大于临界值F0.95(n1,n2), ”相关问题

  • 第1题：

    对于右侧检验而言,拒绝原假设的规则包括()。

    A、检验统计量大于临界值

    B、检验统计量小于临界值

    C、p值大于显著性水平

    D、p值小于显著性水平


    参考答案：AD

  • 第2题：

    考察温度对某一化工产品得率的影响，选了五种不同的温度进行试验，在同一温度下进行了3次试验，试验结果如表所示。
    总和T = 1344,总平均为y = 89. 6,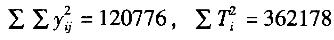 ,请利用以上数据分析下列问题。

    如果在显著性水平0.05时，査表得到的F的临界值是3. 48，那么做方差分析的结论是( )。
    A.在显著性水平0. 05上温度这一因子是显著的
    B.在显著性水平0.05上温度这一因子是不显著的
    C.在显著性水平0.05上不同温度下的平均得率有显著差异
    D.在显著性水平0.05上不同温度下的平均得率无显著差异


    答案：A,C
    解析：
    根据以上结论可知SA =303.6，ST=353.6，所以Se= ST - SA =50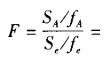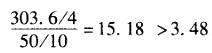， =。因此，在显著性水平0.05上温度这一因子是显著的，即在不同温度下的平均得率有显著差异。

  • 第3题：

    在研究某--问题中使用F检验法，如果在显著性水平a=0. 05的水平下，统计量F大于临界值F0.95(n1，n2)，则在a =0. 01水平下，可能的结论有（ ）。
    A.F > F0.99(n1，n2) B. F ≤ F0.99(n1，n2)
    C. F0.99(n1，n2)>F0.95(n1，n2)D. F0.99(n1，n2) 0.95(n1，n2)
    E. F= F0.99(n1，n2)


    答案：A,B,C,E
    解析：
    F0.99(n1，n2)>F0.95，若F > F0.95，则有可能F>F0.99，也有可能F≤F0.99。

  • 第4题：

    若检验水平为0.05，则统计量应与以下哪个临界值比较

    A．F0.025(2,18)

    B．F0.05(9,18)

    C．F0.05(2,18)

    D．

    E．


    正确答案：C
    答案：C)若H0成立，统计量服从第一自由度为v处理，第二自由度为v误差的F分布。因α＝0.05方差分析为单侧检验，故临界为F0.05(2,18)。

  • 第5题：

    在比较三种加工方法(记为因子A)的试验中，已知三个水平下各进行了6次、5次、4次试 验，作方差分析求得的因子的平方和为155.64，误差平方和为85. 34，则有（ ）。A. F比为 1.823
    B. F比为 1.824
    C. F比为 10. 94
    D.若取显著性水平为0.05，那么当F0.95(2,12)时因子是显著的
    E.若取显著性水平为0.05，那么当F>F0.95(2, 12)时因子是显著的


    答案：C,E
    解析：
    由题可知，水平数r=3，所以因子A平方和的自由度力=r-1=2。由于每一水平下重复次数分别为m1=6, m2 = 5, m3 =4，故总试验次数为n =m1+ m2 +m3 =6+5 + 4 = 15，所以总离差平方和的自由度为fT=n-1=15-1=14，则误差平方和的自由度fe=fT -fA =14-2=12，所以。对给定的显著性水平a，当F>F1-a(fa,fe) 时因子是显著的，所以当a=0.05时，F= 10.94>f0.95(2，12)，即因子是显著的。

相关内容