itgle.com

在抛物线y＝x2(第一象限部分，且2≤8)上求一点，使过该点的切线与直线y＝0，x＝8相交所围成的三角形的面积为最大．

题目

在抛物线y＝x2(第一象限部分，且2≤8)上求一点，使过该点的切线与直线y＝0，x＝8相交所围成的三角形的面积为最大．

相似考题

1.已知曲线C为y= 2x2，直线l为y= 4x．（10分）(1)求由曲线C与直线l所围成的平面图形的面积S；(2)求过曲线C且平行于直线l的切线方程．

2.由抛物线y=x2与三直线x=a，x=a+1，y=0所围成的平面图形，a为下列（　　）值时图形的面积最小。

3.求曲线y=x2与该曲线在x=a(a>0)处的切线与x轴所围的平面图形的面积．

4.设曲线y=f(x)上任一点(x，y)处的切线斜率为(y/x)+x2，且该曲线经过点（1，1/2）。（1）求函数y=f(x)；（2）求由曲线y= f(x），y=O，x=1所围图形绕x轴旋转一周所得旋转体的体积V。

更多“在抛物线y=x2(第一象限部分,且2≤8)上求一点,使过该点的切线与直线y=0,x=8相交所围成的三角形的面 ”相关问题

  • 第1题：

    求曲线y=x2与直线y=0，x=1所围成的平面图形绕x轴旋转一周所得旋转体的体积．


    答案：
    解析：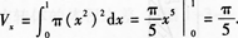

  • 第2题：

    设函数f(x)在定义域I上的导数大于零，若对任意的x0∈I，曲线y=f(x)在点(x0，f(x0))处的切线与直线x=x0及x轴所围成区域的面积恒为4，且f(0)=2，求f(x)的表达式.


    答案：
    解析：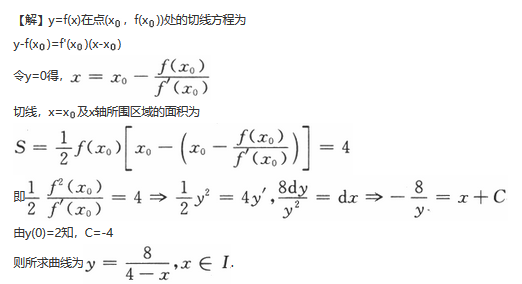

  • 第3题：

    求由曲线y=x2(x≥0)，直线y=1及Y轴围成的平面图形的面积·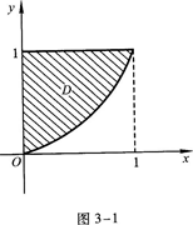


    答案：
    解析：
    y=x2(x≥0)，y=1及y轴围成的平面图形D如图3—1所示．其面积为

  • 第4题：

    如图所示，已知A，B为直线L：y=mx-m+2与抛物线y=x2的两个交点。
    (1)直线ι经过一个定点C，试求出点C的坐标；(2分)
    (2)若m=-1，已知在直线L下方的抛物线上存在一点P(点P与坐标原点0不重合)，且△ABP的面积为（3√13）/2，求点P的坐标。(6分)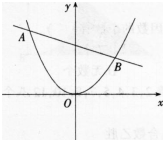


    答案：
    解析：
    (1)直线L：y=m(x-1)+2，当x=1时，y的取值与m无关，此时y=2，所以直线过定点(1，2)；

  • 第5题：

    设P是圆x2+y2=2上的一点，该圆在点P的切线平行于直线x+y+2=0，则点P的坐标为



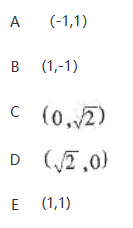    答案：E
    解析：

相关内容