itgle.com
假设ABC公司股票目前的市场价格为24元，而在一年后的价格可能是35元和16元两种情况。现存在一份100股该种股票的看涨期权，期限是一年，执行价格为30元，一年以内公司不会派发股利，无风险利率为每年10%。 要求： （1）根据风险中性定理，计算一份该股票的看涨期权的价值。 （2）根据复制原理，计算一份该股票的看涨期权的价值。 （3）若目前一份100股该股票看涨期权的市场价格为306元，能否创建投资组合进行套利，如果能，应该如何创建该组合。
题目
假设ABC公司股票目前的市场价格为24元，而在一年后的价格可能是35元和16元两种情况。现存在一份100股该种股票的看涨期权，期限是一年，执行价格为30元，一年以内公司不会派发股利，无风险利率为每年10%。
要求：
（1）根据风险中性定理，计算一份该股票的看涨期权的价值。
（2）根据复制原理，计算一份该股票的看涨期权的价值。
（3）若目前一份100股该股票看涨期权的市场价格为306元，能否创建投资组合进行套利，如果能，应该如何创建该组合。
要求：
（1）根据风险中性定理，计算一份该股票的看涨期权的价值。
（2）根据复制原理，计算一份该股票的看涨期权的价值。
（3）若目前一份100股该股票看涨期权的市场价格为306元，能否创建投资组合进行套利，如果能，应该如何创建该组合。
相似考题
更多“假设ABC公司股票目前的市场价格为24元，而在一年后的价格可能是35元和16元两种情况。现存在一份100股该种股票的看涨期权，期限是一年，执行价格为30元，一年以内公司不会派发股利，无风险利率为每年10%。 ”相关问题
-
第1题：
假设ABC公司股票目前的市场价格为28元，而在6个月后的价格可能是40元和20元两种情况。再假定存在一份100股该种股票的看涨期权，期限是半年，执行价格为28元。投资者可以按10%的无风险年利率借款。购进上述股票且按无风险年利率10%借入资金，同时售出一份100股该股票的看涨期权。
要求：
(1)根据单期二叉树期权定价模型，计算一份该股票的看涨期权的价值。
(2)假设股票目前的市场价格、期权执行价格和无风险年利率均保持不变，若把6个月的时间分为两期，每期3个月，若该股票收益率的标准差为0.08，计算每期股价上升百分比和股价下降百分比。
(3)结合(2)分别根据套期保值原理和风险中性原理，计算一份该股票的看涨期权的价值。
正确答案：(1)股价上升百分比＝(40－28)/28＝42.86%，股价下降百分比＝(20－28)/28＝－28.57%
期权的价值C0＝[W1×Cu+(1－w1)×Cd]÷(1+r)
＝
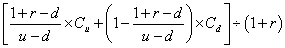
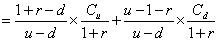
将r＝5%，u＝1.4286，d＝1－0.2857＝0.7143，Cu＝1200，Cd＝0代入上式。
期权的价值C(元)
(2)u＝1+上升百分比＝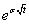
＝
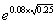＝1.0408，上升百分比＝4.08%
d＝1－下降百分比＝1/u＝1/1.0408＝0.9608，下降百分比＝3.92%
(3)①根据套期保值原理：
套期保值比率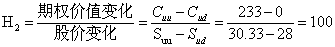
借入资金数额(元)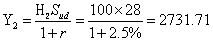
万元，属于沉没成本，即无关成本，不予考虑。另外，部分考生受到了
Cu＝购买股票支出－借款＝H2Su－Y2＝100×29.14－2731.71＝182.29(元)
Cd＝0 _
套期保值比率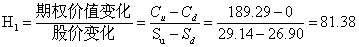
借入资金数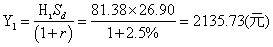
CO＝购买股票支出－借款＝H1SO－Y1＝81.38×28－2135.73＝142.91(元)
②根据风险中性原理：序号 0
1
2
28
29.14
30.33
期权价格
26.90
28
25.85
142.82(或142.91)
182.42(或182.29)
233
期权价格
0
0
0
期望报酬率＝上行概率×股价上升百分比+下行概率×股价下降百分比
＝上行概率×股价上升百分比+(1－上行概率)×股价下降百分比
即：2.5%＝上行概率×4.08%+(1－上行概率)×(－3.92%)
上行概率＝80.25%
期权价值6个月后的期望值＝80.25%×233+(1－80.25%)×0＝186.98(元)
Cu＝186.98/(1+2.5%)＝182.42(元)
期权价值3个月后的期望值＝80.25%×182.42+(1－80.25%)×0＝146.39(元)
期权的现值＝146.39/(1+2.5%)＝142.82(元)。 -
第2题：
假设ABC公司股票目前的市场价格为24元，而在一年后的价格可能是36元和16元两种情况。市场上有两种以该股票为标的资产的期权：看涨期权和看跌期权。每份看涨期权可以买入1股股票，每份看跌期权可卖出1股股票，两种期权执行价格均为30元，到期时间为一年，一年以内公司不会派发股利，无风险利率为每年10%。
要求：
（1）根据复制原理，计算一份该股票的看涨期权的价值，利用看涨期权-看跌期权平价定理，计算看跌期权的价值。
（2）若目前一份该股票看涨期权的市场价格为3.6元，能否创建投资组合进行套利，如果能，应该如何创建该组合。答案：解析：（1）
根据复制原理：
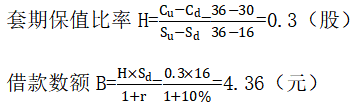
一份该股票的看涨期权的价值=购买股票支出-借款=H×S0-B=0.3×24-4.36=2.84（元）
看跌期权价值=30/（1+10%）+2.84-24=6.11（元）
（2）
由于目前一份该股票看涨期权的市场价格为3.6元，高于期权的价值2.84元，所以，可以创建组合进行套利，以无风险利率借入款项4.36元，购买0.3股股票，同时卖出一份该看涨期权，可以套利=3.6-（0.3×24-4.36）=0.76（元）。 -
第3题：
某公司股票的看涨期权和看跌期权的执行价格均为30元，期权均为欧式期权，期限6个月，6个月的无风险报酬率为3％，目前该股票的价格是32元，看跌期权价格为5元。则看涨期权价格为( )元。A.19．78
B.7．87
C.6．18
D.7．45答案：B解析：根据：标的股票现行价格+看跌期权价格-看涨期权价格=执行价格的现值，
则看涨期权价格=标的股票现行价格+看跌期权价格-执行价格的现值
=32+5-30／(1+3％)
=7．87(元)。 -
第4题：
假设某公司股票目前的市场价格为49.5元，而一年后的价格可能是61.875元和39.6元两种情况。再假定存在一份200股该种股票的看涨期权，期限是一年，执行价格为52.8元。投资者可以购进上述股票且按无风险报价利率10%借入资金，同时售出一份200股该股票的看涨期权。则套期保值比率为（ ）。A.81.48
B.91.48
C.125
D.156答案：A解析：套期保值比率=200×[（61.875-52.8）-0]/（61.875-39.6）=81.48。 -
第5题：
某公司股票看涨期权和看跌期权的执行价格相同，期权均为欧式期权，期限3个月，3个月的无风险利率为2%，目前该股票的价格是38元，看跌期权价格为4.8元，看涨期权价格为1.8元，则期权的执行价格为（ ）元。A、41.82
B、41
C、40.20
D、42.52答案：A解析：根据看涨期权—看跌期权平价定理，期权执行价格的现值=标的资产现行价格+看跌期权价格-看涨期权价格=38+4.8-1.8=41（元），则期权的执行价格=41×（1+2%）=41.82（元）。 -
第6题：
假设A公司目前的股票价格为20元/股，有1股以该股票为标的资产的看涨期权，到期时间为6个月，执行价格为24元， 6个月内公司不派发股利，预计半年后股价有两种可能，上升30%或者下降23%，半年的无风险利率为4%。
要求：（1）用复制原理计算该看涨期权的价值。
（2）用风险中性原理计算该看涨期权的价值。
（3）如果该看涨期权的现行价格为2.5元，请根据套利原理，构建一个投资组合进行套利。答案：解析：（1）复制原理：
上行股价＝20×（1＋30%）＝26（元）
下行股价＝20×（1－23%）＝15.4（元）
套期保值比率H
＝[（26－24）－0]/（26－15.4）＝0.1887
借款数额＝（0.1887×15.4－0）/（1＋4%）＝2.7942（元）
购买股票支出＝0.1887×20＝3.774（元）
期权价值＝3.774－2.7942＝0.98（元）
（2）风险中性原理：
4%＝上行概率×30%＋（1－上行概率）×（－23%）
求得：上行概率＝0.5094
下行概率＝1－0.5094＝0.4906
期权到期时价值
＝0.5094×（26－24）＋0.4906×0
＝1.0188（元）
期权价值＝1.0188/（1＋4%）＝0.98（元）
（3）由于期权价格高于期权价值，因此，套利过程如下：买入0.1887股股票，借入款项2.7942元，同时卖出1股看涨期权，收到2.5元。
结果获利＝2.5＋2.7942－0.1887×20＝1.52（元）。 -
第7题：
某股票当前价格是100元，一年之后预期股价上涨10%或下跌10%，市场无风险利率为8%，运用二又树模型计算执行价格为105元，期限为一年的欧式看涨期权的价值。答案：解析：
-
第8题：
甲公司股票当前每股市价40元，6个月以后股价有两种可能：上升25％或下降20％，市场上有两种以该股票为标的资产的期权：看涨期权和看跌期权。每份看涨期权可买入1股股票，每份看跌期权可卖出1股股票，两种期权执行价格均为45元，到期时间均为6个月，期权到期前，甲公司不派发现金股利，半年无风险报酬率为2％。假设目前市场上每份看涨期权价格2．5元，每份看跌期权价格6．5元，投资者同时卖出1份看涨期权和1份看跌期权，计算确保该组合不亏损的股票价格区间，如果6个月后，标的股票价格实际上涨20％，计算该组合的净损益。（注：计算股票价格区间和组合净损益时，均不考虑期权价格的货币时间价值）
正确答案: 当股价大于执行价格时：
组合净损益=-（股票市价-45）+（2.5+6.5）
根据组合净损益=0，可知，股票市价=54（元）
当股价小于执行价格时：
组合净损益=-（45-股票市价）+9
根据组合净损益=0，可知，股票市价=36（元）
所以，确保该组合不亏损的股票价格区间为36～54元。
如果6个月后的标的股票价格实际上涨20％，即股票价格为40×（1+20％）=48（元），则：
组合净损益=-（48-45）+9=6（元）。 -
第9题：
ABC公司的股票目前的股价为10元，有1股以该股票为标的资产的欧式看涨期权，执行价格为10元，期权价格为2元，到期时间为6个月。假设年无风险利率为4％，计算1股以该股票为标的资产、执行价格为10元、到期时间为6个月的欧式看跌期权的价格；
正确答案:看跌期权价格=看涨期权价格-标的资产价格+执行价格现值=2-10+10／(1+2％)=1．80(元) -
第10题：
问答题如果某公司股票现在的市场价格为32美元，执行价格为30美元的该公司美式股票看涨期权的价格为5.60美元，该期权的有效期还有4个月。同时，市场预期该公司将会在2个月后支付每股1.5美元的股利。假定按连续复利计算的无风险利率为12%（年利率）。要使得市场中不存在无风险套利机会，则该美式看涨期权的价格下限是多少？正确答案： 股利的现值为：
D.1.5*e-0.12*2/12=1.47美元因而，
S.D-Xe-rT=32-1.47-30*e-0.12*4/12=1.71美元
S.Xe-rt=32-e-0.12*2/12=2.59美元
有C>=max（S-D-Xe-rT，S-Xe-rt，0）=2.59美元。
故该美式看涨期权的价格不低于2.59美元。解析： 暂无解析 -
第11题：
问答题K公司目前的股票价格为60美元，此时执行价格为55美元、6个月后到期的K公司股票的欧式看涨期权的市场价格为7.13美元，具有相同标的的股票、执行价格和到期日的欧式看跌期权的市场价格为1.04美元。假设此时市场完全、完善并且不存在套利机会。请问市场中隐含的无风险利率是多少？正确答案： 因为p+S＝c+Xe-rTS=60，X=55，T=0.5，C=7.13，P=1.04
有7.13+55Λ（-0.5r）=1.04+60 所以r等于4%解析： 暂无解析 -
第12题：
问答题假设A公司目前的股票价格为20元/股，以该股票为标的资产的看涨期权到期时间为6个月，执行价格为24元，预计半年后股价有两种可能，上升30%或者下降23%，半年的无风险利率为4%。要求： （1）用复制原理计算该看涨期权的价值； （2）用风险中性原理计算该看涨期权的价值； （3）如果该看涨期权的现行价格为2.5元，请根据套利原理，构建一个投资组合进行套利。正确答案：
(1)复制原理:
上行股价=20×(1+30%)=26(元)
下行股价=20×(1—23%)=15.4(元)
套期保值比率H=[(26-24)-0]/(26-15.4)=0.1887
借款数额=(0.1887×15.4-0)/(1+4%)=2.7942(元)
购买股票支出=0.1887×20=3.774(元)
期权价值=3.774-2.7942=0.98(元)
(2)风险中性原理:
4%=上行概率×30%+(1-上行概率)×(-23%)
求得:上行概率=0.5094下行概率=1-0.5094=0.4906
期权到期时价值=0.5094×(26-24)+0.4906×0=1.0188(元)
期权价值=1.0188/(1十4%)=0.98(元)
(3)由于期权价格高于期权价值,因此,套利过程如下:买人0.1887股股票,借入款项2.7942元,同时卖出1股看涨期权,收到2.5元,结果获利=2.5+2.7942-0.1887×20=1.52(元)解析： 暂无解析 -
第13题：
假设ABC公司股票目前的市场价格为24元，而在一年后的价格可能是35元和16元两种情况。再假定存在一份100股该种股票的看涨期权，期限是一年，执行价格为30元。投资者可以按10%的无风险利率借款。购进上述股票且按无风险利率10%借入资金，同时售出一份100股该股票的看涨期权。
要求：
(1)根据套期保值原理，计算套期保值比率、按无风险利率借入资金的数额以及一份该股票的看涨期权的价值。
(2)根据风险中性原理，计算一份该股票的看涨期权的价值。
(3)若目前一份100股该股票看涨期权的市场价格为306元，按上述组合投资者能否获利。
正确答案：
(1)根据套期保值原理：
套期保值比率H＝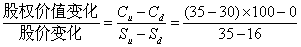
26.32
借入资金数额Y＝
＝382.84(元)
一份该股票的看涨期权的价值＝购买股票支出－借款＝HSO－Y＝26.32×24—382.84＝248.84(元)。
(2)根据风险中性原理：
期望报酬率＝上行概率×股价上升百分比+下行概率×股价下降百分比＝上行概率×股价上升百分比+(1－上行概率)×股价下降百分比
股价上升百分比＝(35—24)/24＝45.83%，股价下降百分比＝(16—24)/24＝－33.33%
假设上行概率为w。，则：
r＝W1×45.83%+(1－W1)×(－33.33%)
即：10%＝W1×45.83%+(1－W1)×(－33.33%)
求得：W1＝54.74%
期权一年后的期望价值＝54.74%×500+(1—54.74%)×0＝273.7(元)
期权的现值＝273.7/(1+10%)＝248.82(元)。
(3)由于目前一份100股该股票看涨期权的市场价格为306元，高于期权的价值248.82元，所以，该组合可以盈利。 -
第14题：
甲公司股票当前每股市价40 元，6 个月以后股价有两种可能，上升25%或下降20%，市场上有两种以该股票为标的资产的期权：看涨期权和看跌期权，每份看涨期权可以买入1 股股票，每份看跌期权可以卖出1 股股票，两种期权执行价格均为45 元，到期时间均为6 个月，期权到期前，甲公司不派发现金股利，半年无风险报酬率为2%。
要求：
(2)假设市场上每份看涨期权价格为2.5 元，每份看跌期权价格1.5 元，投资者同时卖出一份看涨期权和一份看跌期权，计算确保该组合不亏损的股票价格区间，如果6 个月后的标的股票价格实际上涨20%，计算该组合的净损益。(注：计算股票价格区间和组合净损益时，均不考虑期权价格的货币时间价值)。
(2)利用风险中性原理，计算看涨期权的股价上行时到期日价值、上行概率及期权价值，利用看涨期
权—看跌期权平价原理，计算看跌期权的期权价值。答案：解析：(1)卖出看涨期权的净损益=—Ma*(股票市价—执行价格，0)+期权价格=—Ma*(股票市价—45，0)+2.5
卖出看跌期权的净损益=—Ma*(执行价格—股票市价，0)+期权价格=—Ma*(45-股票市价，0)+1.5
组合净损益=—Ma*(股票市价-45,0)—Ma*(45-股票市价，0)+4
当股价大于执行价格时：
组合净损益=—(股票市价-45)+4
根据组合净损益=0 可知，股票市价=49(元)
当股价小于执行价格时：
组合净损益=—Ma*(45-股票市价)+4
根据组合净损益=0 可知，股票市价=41(元)
所以，确保该组合不亏损的股票价格区间为大于或等于41 元、小于或等于49 元。
如果6 个月后的标的股票价格实际上涨20%，即股票价格为48 元，则：
组合净损益=—(48-45)+4=1(元)
(2)看涨期权的股价上行时到期日价值=40*(1+25%)—45=5(元)
2%=上行概率*25%—(1-上行概率)*20%
解得上行概率=0.4889
由于股价下行时到期日价值=0，所以看涨期权价值=(5*0.4889)/(1+2%)=2.40(元)
看跌期权价值=45/(1+2%)+2.40-40=6.52(元) -
第15题：
假设ABC公司股票目前的市场价格为24元，而在一年后的价格可能是30元和19.2元两种情况。现存在一份100股该种股票的看涨期权，期限是一年，执行价格为25元，一年以内公司不会派发股利，无风险年报价利率为10%。
要求：
（1）根据风险中性原理，计算一份该股票的看涨期权的价值。
（2）根据复制原理，计算一份该股票的看涨期权的价值。
（3）若目前一份100股该股票看涨期权的市场价格为306元，能否构建投资组合进行套利，如果能，应该如何构建该组合。答案：解析：（1）根据风险中性概率公式：
期望报酬率=上行概率×股价上升百分比+下行概率×股价下降百分比
=上行概率×股价上升百分比+（1-上行概率）×股价下降百分比
股价上升百分比=（30-24）/24=25%，股价下降百分比=（19.2-24）/24=-20%
假设上行概率为P，则：
r=P×25%+（1-P）×（-20%）
即：10%=P×25%+（1-P）×（-20%）
求得：P=66.67%
期权一年后的期望价值=66.67%×（30-25）×100+（1-66.67%）×0=333.35（元）
期权价值=333.35/（1+10%）=303.05（元）。
（2）根据复制原理：
套期保值比率H=[（30-25）-0]/（30-19.2）×100=46.3（股）
借款数额B=（46.3×19.2-0）/（1+10%）=808.15（元）
一份该股票的看涨期权的价值=购买股票支出-借款=H×Sd-B=46.3×24-808.15=303.05（元）。
（3）由于目前一份100股该股票看涨期权的市场价格为306元，高于期权的价值303.05元，所以，可以创建组合进行套利，以无风险利率借入款项808.15元，购买46.3股股票，同时卖出一份该看涨期权，可以套利306-（46.3×24-808.15）=2.95（元）。
-
第16题：
假设目前市场上以甲公司股票为标的的每份看涨期权价格3元，每份看跌期权价格7元，两种期权执行价格均为52元，到期时间均为6个月，甲公司不派发现金股利，年无风险利率为8%。
要求：
（1）利用看涨看跌平价定理计算股票当前的价格；
（2）如果甲公司的股票价格出现波动，简要说明波动幅度和投资人应该采取的措施；
（3）A投资人购买甲公司的一股股票持有；B投资人同时购买甲公司的一股股票和一份以该股票为标的的看跌期权。简要分析A投资人和B投资人的风险和收益。答案：解析：（1）根据平价定理，看涨期权的价格-看跌期权的价格=当前股票价格-执行价格的现值
3-7=当前股票的价格-52/（1+4%），当前股票的价=46（元）；
（2）看涨期权的价格+看跌期权的价格=3+7=10（元）
如果股价超过执行价格的幅度大于10元，即股价高于62元或者低于42元，应当采取多头对敲策略；如果估价超过执行价格的幅度低于10元，即股价在42元到62元之间，应当采取空头对敲的策略；
（3）B投资人采取的投资策略为保护性看跌期权；A投资人的风险和收益都要大于B投资人。保护性看跌期权净收益波动的幅度要远远低于股票收益波动的幅度。当股票价格上升时，保护性看跌期权的净收益要低于购买股票的净收益；当股票价格下降时，保护性看跌期权的净损失也同样低于购买股票的净损失。所以当股价下降时，看跌期权对于股价有一定的保护作用，但同时也降低了其收益。
当股票价格下降10元时，到期日股价=46-10=36（元），低于执行价格，保护性看跌期权净损益52-46-7=-1（元）；购买股票的净损益=-10元；
当股票价格下降5元时，到期日股价=46-5=41（元），保护性看跌期权净损益52-46-7=-1（元）；购买股票的净损益=-5元；
当股票价格不变时，到期日股价=46（元），保护性看跌期权净损益=52-46-7=-1（元）；购买股票的净损益=0元；
当股票价格上升5元时，到期日股价=46+5=51（元），低于执行价格，保护性看跌期权净损益52-46-7=-1（元）；购买股票的净损益=5元；
当股票价格上升10元时，到期日股价=46+10=56（元），高于执行价格，保护性看跌期权净损益=56-46-7=3（元），购买股票的净损益=10元；
当股票价格上升15元时，到期日股价=46+15=61（元），高于执行价格，保护性看跌期权净损益=61-46-7=8（元），购买股票的净损益=15元。
从上面列举的数字可以看到，保护性看跌期权波动的幅度要低于股价波动的幅度，所以说A投资人的风险要高于B投资人的风险；另外，当股价上升时，购买股票的净收益也要大于保护性看跌期权这个组合。综合来说，购买股票的风险和收益都要大于保护性看跌期权。这就是所谓的高风险高收益。 -
第17题：
（2018年）甲公司是一家上市公司，上年刚发现金股利2.2元，资本成本10%，甲公司未来股利增长率6%，股票现在市价为50元，市场上有两种以甲公司股票为标的资产的期权。欧式看涨期权和欧式看跌期权，每份看涨期权可买入1股股票，每份看跌期权可卖出1股股票，看涨期权5元/份，看跌期权3元/份。期权一年后到期，执行价格为50元。小王和小张都花了53000元，小王买了1000股甲公司股票及1000份看跌期权，小张买了看涨期权10600份。
要求：
（1）利用股利增长模型计算一年后股票内在价值。
（2）根据第一问结果计算一年后小王和小张的投资净损益。
（3）若一年后甲公司股票跌至40元/股，计算小王和小张的投资净损益。答案：解析：（1）一年后股票内在价值
＝[2.2×（1＋6%）/（10%－6%）] ×（1＋6%）＝61.8（元）
（2）小王的投资是保护性看跌期权投资策略，一年后股价61.8元高于执行价格50元，则：
组合净损益＝组合收入－组合成本＝[61.8－（50＋3）]×1000＝8800（元）
小张购买看涨期权的投资损益＝[（61.8－50）－5]×10600＝72080（元）
（3）小王的投资是保护性看跌期权投资策略，如果股价跌至40元/股，低于执行价格，则：
组合净损益＝组合收入－组合成本＝[50－（50＋3）]×1000＝－3000（元）
小张购买看涨期权的投资损益＝（0－5）×10600＝－53000（元） -
第18题：
假设某公司股票目前的市场价格为45元，6个月后的价格可能是55元和35元两种情况。有1股以该股票为标的资产的看涨期权，到期时间是6个月，执行价格为48元。投资者可以购进上述股票且按无风险利率10%借入资金，同时售出一份该股票的看涨期权。则套期保值比率为（ ）。A、0.35
B、0.2
C、0.1
D、0.5答案：A解析：套期保值比率=
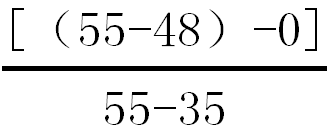
=0.35。 -
第19题：
假设IBM股票（不支付红利）的市场价格为50美元，无风险利率为12%，股票的年波动率为10%，那么价格为50美元，期限为一年的欧式看涨期权和看跌期权的理论价格分别是（ ）。A.5.92，0.27
B.6.21，2.12
C.6.15，1.25
D.0.1，5.12答案：A解析：已知：S=50美元；K=50美元；T=1年；r=0.12；σ=0.1。
故有：N（d1）=0.8944N（d2）=0.8749
如此，欧式看涨期权和看跌期权的理论价格分别为：
C=50×0.8944-50×0.8749e-0.12×1=5.92（美元）
P=50×（1-0.8749）e-0.12×1-50×（1-0.8944）
=0.27（美元）
考点：B-S-M模型 -
第20题：
K公司目前的股票价格为60美元，此时执行价格为55美元、6个月后到期的K公司股票的欧式看涨期权的市场价格为7.13美元，具有相同标的的股票、执行价格和到期日的欧式看跌期权的市场价格为1.04美元。假设此时市场完全、完善并且不存在套利机会。请问市场中隐含的无风险利率是多少？
正确答案:因为p+S＝c+Xe-rTS=60，X=55，T=0.5，C=7.13，P=1.04
有7.13+55Λ（-0.5r）=1.04+60 所以r等于4% -
第21题：
问答题ABC公司的股票目前的股价为10元，有1股以该股票为标的资产的欧式看涨期权，执行价格为10元，期权价格为2元，到期时间为6个月。假设年无风险利率为4％，计算1股以该股票为标的资产、执行价格为10元、到期时间为6个月的欧式看跌期权的价格；正确答案： 看跌期权价格=看涨期权价格-标的资产价格+执行价格现值=2-10+10／(1+2％)=1．80(元)解析： 暂无解析 -
第22题：
单选题假设ABC公司股票目前的市场价格50元，而在一年后的价格可能是60元或40元两种情况。再假定存在一份100股该种股票的看涨期权，期限是一年，执行价格为50元。投资者可以按10%的无风险利率借款。购进上述股票且按无风险利率10%借入资金，同时售出一份100股该股票的看涨期权。则按照复制原理，下列说法错误的是（）。A购买股票的数量为50股
B借款的金额是1818元
C期权的价值为682元
D期权的价值为844元
正确答案： B解析： 暂无解析 -
第23题：
问答题计算分析题：假设A公司日前的股票价格为20元／股，以该股票为标的资产的看涨期权到期时间为6个月，执行价格为24元，6个月以内公司不会派发股利，预计半年后股价有两种可能，上升30%或者下降23%，半年的无风险利率为1%。要求：（1）应复制原理计算该看涨期权的价值；（2）用风险中性原理计算该看涨期权的价值；（3）如果该看涨期权的现行价格为2.5元，请根据套利原理，构建一个投资组合进行套利。正确答案： （1）复制原理：上行股价=20×（1+30%）=26（元）下行股价=20×（1-23%）=15.4（元）套期保值比率H=［（26-24）-0］／（26-15.4）=0.1887借款数额=（0.1887×15.4-0）／（1+4%）=2.7942（元）购买股票支出=0.1887×20=3.774（元）期权价值=3.774-2.7942-0.98（元）（2）风险中性原理：4%=上行概率×30%+（1-上行概率）×（-23%）求得：上行概率-0.5094下行概率=1-0.5094=0.4906期权到期日价值=0.5094×（26-24）+0.4906×0=1.0188（元）期权价值=1.0188/（1+4%）=0.98（元）（3）由于期权价格高于期权价值，因此，套利过程如下：买入0.1887股股票，借入款项2.7942元，同时卖出1股看涨期权，收到2.5元，结果获利=2.5+2.7942-0.1887×20=1.52（元）。解析： 先根据期权价格和期权价值的大小关系，确定是买入还是卖出期权：期权价格大于期权价值则卖出期权，期权价格小于期权价值则买入期权。买入股票与借入款项的组合到期日流量与买入期权的到期日流量相同，因此可以与卖出期权构建套利组合，使得到期日现金流量始终为0，即卖出期权的话，则需要买入股票同时借入款项构建套利组合。同理，如果是买入期权，则需要卖空股票同时贷出款项构建套利组合。