完全随机设计资料的方差分析的基本思想是A.总变异等于组间变异和组内变异之和 B.总变异等于组间变异和组内变异之积 C.总均方等于组间均方和组内均方之积 D.总均方等于组间均方和组内均方之和 E.总变异等于处理组间变异、区组间变异和误差变异之和
题目
B.总变异等于组间变异和组内变异之积
C.总均方等于组间均方和组内均方之积
D.总均方等于组间均方和组内均方之和
E.总变异等于处理组间变异、区组间变异和误差变异之和
相似考题
更多“完全随机设计资料的方差分析的基本思想是”相关问题
-
第1题:
完全随机设计资料方差分析的总变异分解为
A.

B.

C.

D.

E.
 参考答案:A
参考答案:A
-
第2题:
首选的统计检验方法是
A.多个样本率比较的χ2检验
B.4×3表χ2检验
C.完全随机设计资料的方差分析
D.配伍组设计资料的方差分析
E.配伍设计资料的秩和检验
正确答案:D
-
第3题:
在完全随机设计的方差分析中,必然有 ( )
 正确答案:C
正确答案:C
-
第4题:
某地两年的痢疾菌型分布 检验两年的菌型构成比有无差别,应选择的统计方法是
检验两年的菌型构成比有无差别,应选择的统计方法是
A.配对计数资料χ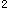 检验
检验
B.完全随机设计方差分析
C.随机分组设计方差分析
D.行×列表资料χ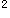 检验
检验
E.四格表资料χ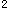 检验答案:D解析:
检验答案:D解析: -
第5题:
完全随机设计资料的方差分析结果所比较的临界值是F0.05,(2,12),据此可推断资料的总例数为A.10
B.12
C.13
D.15
E.16答案:D解析:F0.05(v组间,v组内)=F0.05,(2,12),所以可知v组间=2,v组内=12。又v组内=N-k,v组间=k-1。将数值代入公式可求得k=3,N=15。 -
第6题:
完全随机设计资料方差分析的总变异分解为
正确答案:C -
第7题:
简述方差分析的基本思想。
正确答案: 一方面,同一总体内部的各数据是不同的,其差异可以看成是由于随机因素造成的;另一方面,不同总体的各数据也是不同的,这既可能是由于总体数据的平均水平不同造成的,也有可能是由于随机因素造成的。要判断随机因素和总体均值差别哪个是造成各数据不同的主要原因,在假设遇到的都是正态总体、各总体的方差无显著差异和各数据相互独立的条件下,可进行正态总体均值是否相等的检验,即用F检验解决系统因素是否是造成数据差异的主要原因的问题 -
第8题:
随机区组设计的实验资料,如果用随机区组设计的方差分析检验区组效应,其结果为无统计学意义,请问:能否用完全随机设计的方差分析?
正确答案: ①随机区组设计的实验资料,若用随机区组设计的方差分析检验区组效应,结果无统计学意义,对该资料而言是不能用完全随机设计的方差分析进行统计分析的
②因为完全随机设计的方差分析要求资料各组独立,而随机区组设计各组间是不独立的,所以即便区组效应无统计学意义,也不能改变其随机区组设计的检验方式。 -
第9题:
完全随机设计资料的方差分析结果所比较的临界值是:F(2,12)0.05,据此可推断资料的总例数为()
- A、12
- B、15
- C、16
- D、13
- E、10
正确答案:B -
第10题:
单选题完全随机设计资料方差分析的总变异分解为()AA
BB
CC
DD
EE
正确答案: C解析: 暂无解析 -
第11题:
单选题配对设计的两组资料,如对两均数差别进行假设检验,则可用()。A配对t检验和随机区组方差分析
B成组t检验和随机区组方差分析
C成组t检验和完全随机设计方差分析
D配对t检验和完全随机设计方差分析
E只能用配对t检验
正确答案: B解析: 暂无解析 -
第12题:
单选题完全随机设计资料的方差分析,其组内自由度的计算公式是()AN-1
Bk-1
CN-k
DN-k-1
EN-k+1
正确答案: A解析: 暂无解析 -
第13题:
完全随机设计资料方差分析的变异分解为
A、SS
 =SS
=SS +SS
+SS
B、MS
 =MS
=MS +MS
+MS
C、SS
 >SS
>SS
D、MS
 <MS
<MS
E、V
 <V
<V 参考答案:A
参考答案:A
-
第14题:
完全随机设计方差分析中的组内均方
 正确答案:D
正确答案:D
-
第15题:
完全随机设计资料的方差分析结果所比较的临界值是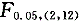 ,据此可推断资料的总例数为A.12
,据此可推断资料的总例数为A.12
B.15
C.16
D.13
E.10答案:B解析:ν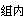 =N-k=12,ν
=N-k=12,ν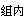 =k-1=2。
=k-1=2。 -
第16题:
完全随机设计资料的方差分析,其组内自由度的计算公式是A.N-k-1
B.k-1
C.N-1
D.N-k+1
E.N-k答案:E解析: -
第17题:
完全随机设计资料的方差分析中,有A.MS <MS
<MS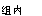
B.SS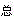 =SS
=SS +SS
+SS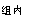
C.SS >SS
>SS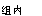
D.MS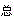 =MS
=MS +MS
+MS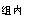
E.υ >
>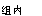 答案:B解析:
答案:B解析: -
第18题:
完全随机设计的方差分析的基本思想是()
- A、SS组内<SS组间
- B、MS组内<MS组间
- C、MS总>MS组内﹢MS组间
- D、SS总>SS组内﹢SS组间
- E、SS总=SS组内﹢SS组间
正确答案:E -
第19题:
完全随机设计资料方差分析中要求各组均数相差不大。
正确答案:错误 -
第20题:
两因素析因设计的研究资料,可以采用完全随机设计的方差分析比较各组别的差异,但不可以分析交互作用。
正确答案:正确 -
第21题:
什么是方差分析?方差分析的基本思想是什么?进行方差分析一般有哪些步骤?
正确答案: (1)方差分析是对两个或多个样本平均数差异显著性检验的方法。
(2)方差分析的基本思想是将测量数据的总变异按照变异来源分为处理效应和误差效应,并作出数量估计,在一定显著水平下进行比较,从而检验处理效应是否显著。
(3)方差分析的基本步骤如下:
①将样本数据的总平方和与自由度分解为各变异因素的平方和与自由度。
②列方差分析表进行F检验,分析各变异因素在总变异中的重要程度。
③若F检验显著,对个处理平均数进行多重比较。 -
第22题:
配伍题完全随机设计资料方差分析的总变异分解为|随机区组设计资料的方差分析总变异的分解为正确答案: A解析: 暂无解析 -
第23题:
单选题完全随机设计的方差分析的基本思想是()ASS组内<SS组间
BMS组内<MS组间
CMS总>MS组内﹢MS组间
DSS总>SS组内﹢SS组间
ESS总=SS组内﹢SS组间
正确答案: B解析: 暂无解析 -
第24题:
问答题什么是方差分析?方差分析的基本思想是什么?进行方差分析一般有哪些步骤?正确答案: (1)方差分析是对两个或多个样本平均数差异显著性检验的方法。
(2)方差分析的基本思想是将测量数据的总变异按照变异来源分为处理效应和误差效应,并作出数量估计,在一定显著水平下进行比较,从而检验处理效应是否显著。
(3)方差分析的基本步骤如下:
①将样本数据的总平方和与自由度分解为各变异因素的平方和与自由度。
②列方差分析表进行F检验,分析各变异因素在总变异中的重要程度。
③若F检验显著,对个处理平均数进行多重比较。解析: 暂无解析
