一点电荷q位于立方体的中心,则通过该立方体六个表面中某一个面的电通量为_______。
题目
一点电荷q位于立方体的中心,则通过该立方体六个表面中某一个面的电通量为_______。
相似考题
参考答案和解析
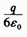
更多“一点电荷q位于立方体的中心,则通过该立方体六个表面中某一个面的电通量为_______。 ”相关问题
-
第1题:
一半径为R的均匀带电球壳,在其球心O处放置一点电荷q,该电荷受的电场力为零,若该电荷偏离球心O,则该电荷q的受力情况为()。A、变大
B、变小
C、不变
D、无法判断
参考答案:A
-
第2题:
 封闭球面,则通过该球面的电通量为:
封闭球面,则通过该球面的电通量为:
 答案:C解析:真空中通过任意闭合曲面的电通量所包围的电荷的代数和。
答案:C解析:真空中通过任意闭合曲面的电通量所包围的电荷的代数和。
答案:C -
第3题:
电场中有个闭合球面,球面所包围的电荷电量为+q1,球面外电荷的电量为-q2,则通过该球面的电通量Φ是( )。A.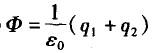
B.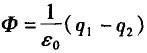
C.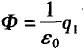
D.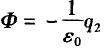 答案:C解析:
答案:C解析: -
第4题:
设真空中点电荷+q1和点电荷+q2相距2a,且q2=2q1,以+q1为中心、a为半径形成封闭球面,则通过该球面的电通量为()。
A. 3q B. 2q1 C. q1 D.0答案:C解析:。
提示:根据库仑定律分析。 -
第5题:
若高斯面的电通量为零,则面内处处无电荷。
正确答案:错误 -
第6题:
点电荷q位于一个边长为a的立方体中心,试求在该点电荷电场中穿过立方体一面的电通量是多少?
正确答案:当点电荷放在中心时,电通量要穿过6个面,通过每一面的电通量为Φ1=Φe/6=q/6ε0. -
第7题:
将512个体积为1立方厘米的小立方体,合成一个边长为8厘米的大立方体,并在大立方体的六个面上分别刷上不同的颜色,再分开为原来的小立方体,则被刷上两种不同颜色的小立方体的数目是()个。
- A、72
- B、80
- C、88
- D、96
正确答案:A -
第8题:
立方体(Cube)是对数据库中数据进行整合后产生的多维数据文件,固定报表的数据来源于立方体。目前报表子系统向征信分中心下发()个立方体文件。
- A、八个
- B、六个
- C、五个
- D、七个
正确答案:D -
第9题:
关于高斯定理,下列说法中正确的是() (1)高斯面上的电场强度只与面内的电荷有关,与面外的电荷无关; (2)高斯面上的电场强度与面内和面外的电荷都有关系; (3)通过高斯面的电通量只与面内的电荷有关,与面外的电荷无关; (4)若正电荷在高斯面之内,则通过高斯面的电通量为正;若正电荷在高斯面之外,则通过高斯面的电通量为负。
- A、(1)和(4)正确
- B、(2)和(3)正确
- C、(1)和(3)正确
- D、(2)和(4)正确
正确答案:B -
第10题:
如果将源点电荷移到立方体的的一个角上,这时通过立方体各面的电通量是多少?
正确答案:当点电荷放在一个顶角时,电通量要穿过8个卦限,立方体的3个面在一个卦限中,通过每个面的电通量为Φ1=Φe/24=q/24ε0;立方体的另外3个面的法向与电力线垂直,通过每个面的电通量为零. -
第11题:
判断题体心立方晶格的原子位于立方体的八个顶角及立方体的中心。A对
B错
正确答案: 对解析: 暂无解析 -
第12题:
单选题设真空中点电荷+q1和点电荷+q2相距2a,且q2=2q1,以+q1为中心、a为半径形成封闭球面,则通过该球面的电通量为()。A3q
B2q1
Cq1
D0
正确答案: D解析: 暂无解析 -
第13题:
将一重100N、边长为20cm的均匀立方体,放置在水平的小桌面正中. (1)若小桌面的边长为10cm,则立方体对桌面压强是多少?
(2)若小桌面边长为30cm,则立方体对桌面的压强是多大?
