试用区间套定理证明: 直线上有界无限集至少有一个聚点.
题目
试用区间套定理证明: 直线上有界无限集至少有一个聚点.
相似考题
参考答案和解析
用反证法 假设定理的结论不成立,即不能用 中有限个开区间来覆盖 [ a , b ] . 将 [ a , b ] 等分为两个子区间,则其中至少有一个子区间不能用 H 中有限个开区间来覆盖.记这个子区间为 [ a 1 , b 1 ] ,则 [ a 1 , b 1 ] Ì [ a , b ] ,且 . 再将 [ a 1 , b 1 ] 等分为两个子区间,同样,其中至少有一个子区间不能用 H 中有限个开区间来覆盖.记这个子区间为 [ a 2 , b 2 ] ,则 [ a 2 , b 2 ] Ì [ a 1 , b 1 ] ,且 . 重复上述步骤并不断地进行下去,则得到一个闭区间列 {[ a n , b n ]} ,它满足 [a n+1 , b n+1 ] Ì [ a n , b n ] , n=1,2,... 即 {[ a n , b n ]} 是区间套,且其中每一个闭区间都不能用 H 中有限个开区间来覆盖 由区间套定理,存在唯一的一点 ξ ∈ [a n ,b n ],n=1,2,... 由于 H 是 [ a , b ] ,的一个开覆盖,故存在开区间 ( a , b )∈H ,使 ξ ∈( a , b ) .由定理 5 推论,当 充分大时有 {[a n ,b n ]} Ì ( a , b ) ,这表明 [a n ,b n ] 只须用 H 中的一个开区间 ( a , b ) 就能覆盖,与挑选 [a n ,b n ] 时的假设 “ 不能用 H 中有限个开区间来覆盖 ” 相矛盾.从而证得必存在属于 H 的有限个开区间能覆盖 [ a , b ] . 注 定理结论对开区间则不一定成立.即 不一定能选出有限个区间来覆盖。
更多“试用区间套定理证明: 直线上有界无限集至少有一个聚点.”相关问题
-
第1题:
在平面有界区域内,由连续曲线C围成一个封闭图形。证明:存在实数ξ使直线y=x+ξ平分该图形的面积。答案:解析:
-
第2题:
可行解集非空时,则在极点上至少有一点达到最优值可能无穷( )答案:错解析: -
第3题:
若点的投影有一个不在直线的同名投影上,则该点()此直线上。
正确答案:必不在 -
第4题:
一个函数的返回值有()个。
- A、无
- B、至少有一个
- C、只能有一个
- D、无限个
正确答案:C -
第5题:
若点在直线上,则点的投影必在直线的同名投影上。并将线段的同名投影分割成与空间相同的比例。即:()(定比定理)。
正确答案:AC/CB=ac/cb=a'c'/c'b' -
第6题:
可行解集非空时,则在极点上至少有一点达到最优值()
正确答案:错误 -
第7题:
复变函数在有界闭集上是连续的。
正确答案:正确 -
第8题:
单选题哈勃的实验观测表明()。A宇宙有一个结束
B宇宙有一个开端
C宇宙有界无限
D宇宙始于无序
正确答案: D解析: 暂无解析 -
第9题:
单选题下列命题正确的是( )A分段函数,必存在间断点
B单调有界函数无第二类间断点
C在开区间上连续,则在该区间必取得最大值和最小值
D闭区间上有间断点的函数一定有界
正确答案: D解析: -
第10题:
填空题若点在直线上,则点的投影必在直线的同名投影上。并将线段的同名投影分割成与空间相同的比例。即:()(定比定理)。正确答案: AC/CB=ac/cb=a'c'/c'b'解析: 暂无解析 -
第11题:
判断题复变函数在有界闭集上的模无最大值。A对
B错
正确答案: 错解析: 暂无解析 -
第12题:
单选题直线的透视消失于直线上无限远点的透视F点,称为直线的()点。A灭
B不可见
C透视
D无限远
正确答案: D解析: 暂无解析 -
第13题:
罗尔定理:设函数(x)满足条件:(1)在闭区间[a,b]上连续;(2)在开区间(a,b)内可导;(3)(a)=(b),则在(a,b)内至少存在一点ξ,使得,′(ξ)=0。证明这个定理并说明其几何意义。答案:解析:
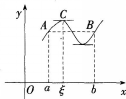
-
第14题:
函数y=sinx在区间[0,π]上满足罗尔定理的ξ=( ) 答案:C解析:
答案:C解析: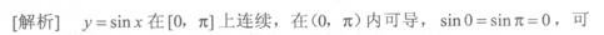
-
第15题:
直线上离画面无限远的点,其透视称为直线上的()。
- A、基灭点
- B、灭点
- C、心点
- D、远点
正确答案:B -
第16题:
哈勃的实验观测表明()。
- A、宇宙有一个结束
- B、宇宙有一个开端
- C、宇宙有界无限
- D、宇宙始于无序
正确答案:B -
第17题:
“在平面内过已知直线外一点,只有一条直线与已知直线平行”是下面哪一项公理?()
- A、墨菲定理
- B、阿基米德定律
- C、欧几里得平行公理
- D、勾股定理
正确答案:C -
第18题:
毕达哥拉斯定理是()
- A、平方反比定律
- B、无限循环小数定理
- C、勾股定理
正确答案:C -
第19题:
复变函数在有界闭集上的模无最大值。
正确答案:错误 -
第20题:
填空题若点的投影有一个不在直线的同名投影上,则该点()此直线上。正确答案: 必不在解析: 暂无解析 -
第21题:
单选题“在平面内过已知直线外一点,只有一条直线与已知直线平行”是下面哪一项公理?()A墨菲定理
B阿基米德定律
C欧几里得平行公理
D勾股定理
正确答案: B解析: 暂无解析 -
第22题:
判断题复变函数在有界闭集上是连续的。A对
B错
正确答案: 错解析: 暂无解析 -
第23题:
问答题设f(x)在闭区间[0,c]上连续,其导数f′(x)在开区间(0,c)内存在且单调减少,f(0)=0,试应用拉格朗日中值定理证明不等式:f(a+b)≤f(a)+f(b),其中a,b满足条件0≤a≤b≤a+b≤c。正确答案:
f(a+b)-f(a)-f(b)=[f(a+b)-f(b)]-[f(a)-f(0)]。
因为f(x)在区间(0,a),(b,a+b)上满足拉格朗日中值定理,因此分别存在ξ∈(0,a),η∈(b,a+b),使得f(a)-f(0)=af′(ξ),f(a+b)-f(b)=af′(η),从而有f(a+b)-f(a)-f(b)=a[f′(η)-f′(ξ)]。
又f′(x)在(0,c)上单调减少,故f′(η)≤f′(ξ),故f(a+b)-f(a)-f(b)≤0,即f(a+b)≤f(a)+f(b)。解析: 暂无解析 -
第24题:
单选题以下说法不正确的是()。A点的投影永远是点
B直线的投影可以聚成点
C平面的投影可以聚成直线
D以上说法都不对
正确答案: D解析: 暂无解析
