创建一个4阶魔术矩阵A与单位矩阵B，并分别计算两矩阵之和、矩阵相乘、矩阵点乘、A矩阵乘方、A矩阵装置。

题目

相似考题

1.教材分析使用的()。A、可达矩阵B、单位矩阵C、加法矩阵D、零矩阵

2.设A为n阶对称矩阵,则A是正定矩阵的充分必要条件是( ).A.二次型xTAx的负惯性指数零B.存在n阶矩阵C,使得A=CTCC.A没有负特征值D.A与单位矩阵合同

3.对矩阵版的描述,正确的是()A.每块矩阵版提供两个8X4交换矩阵B.每块矩阵版提供一个8X4交换矩阵C.每块矩阵版提供两个8X8交换矩阵D.每块矩阵版提供一个8X8交换矩阵

4.常用的特殊矩阵有哪些()。A、单位矩阵B、零矩阵C、对角矩阵D、空矩阵

更多“创建一个4阶魔术矩阵A与单位矩阵B，并分别计算两矩阵之和、矩阵相乘、矩阵点乘、A矩阵乘方、A矩阵装置。”相关问题

第1题：

已知4阶矩阵A~B，A的特征值为3,4,5,6，E为4阶单位矩阵，则|B-E|=（）

A.20
B.60
C.120
D.360

答案：C
解析：
第2题：

设A=，E为三阶单位矩阵.
　　(Ⅰ)求方程组Ax=0的一个基础解系；
　　(Ⅱ)求满足AB=E的所有矩阵B.

答案：
解析：
【分析】(Ⅰ)是基础题，化为行最简即可.
关于(Ⅱ)中矩阵B，其实就是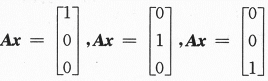三个方程组的求解问题.
【解】(Ⅰ)对矩阵A作初等行变换，得
第3题：

设A为n阶非奇异矩阵，α为n维列向量，b为常数.记分块矩阵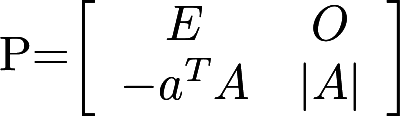.其中A*是矩阵A的伴随矩阵，E是n阶单位矩阵. （1）计算并化简PQ；（2）证明：矩阵Q可逆的充分必要条件是.

答案：
解析：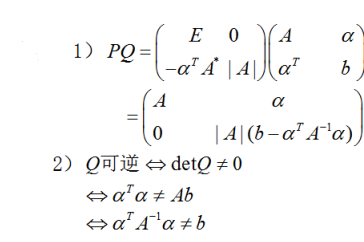
第4题：

设矩阵是4阶非零矩阵, 且满足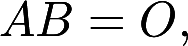证明矩阵B的秩

答案：
解析：
第5题：

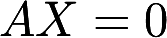设，E为3阶单位矩阵（1）求方程组的一个基础解系；（2）求满足的所有矩阵B

答案：
解析：
第6题：

设A，B，C均为n阶矩阵，E为n阶单位矩阵，若B=E+AB，C=A+CA，则B-C=

A.E
B.-E
C.A
D.-A

答案：A
解析：
第7题：

设A为n阶实对称矩阵,下列结论不正确的是().

A.矩阵A与单位矩阵E合同
B.矩阵A的特征值都是实数
C.存在可逆矩阵P,使P^-1AP为对角阵
D.存在正交阵Q,使Q^TAQ为对角阵

答案：A
解析：
根据实对称矩阵的性质，显然(B)、(C)、(D)都是正确的，但实对称矩阵不一定是正定矩阵，所以A不一定与单位矩阵合同，选(A).
第8题：

设A为4阶魔术矩阵，分别对A进行如下操作：求矩阵A的逆；求矩阵A的行列式；求矩阵A的秩；求矩阵A的迹；

正确答案: >>A=magic（4）
>>B=inv（A）
>>C=det（A）
>>D=rank（A）
>>E=trace（A）
第9题：

问答题
创建一个4阶魔术矩阵A与单位矩阵B，并分别计算两矩阵之和、矩阵相乘、矩阵点乘、A矩阵乘方、A矩阵装置。

正确答案： >>A=magic（4）
>>B=eye（4）
>>C=A+B
>>D=A*B
>>E=A.*B
>>F=A^2
>>G=A’
解析：暂无解析
第10题：

问答题
设A是n阶矩阵，且满足Am＝E，其中m为整数，E为n阶单位矩阵。令将A中的元素aij换成它的代数余子式Aij而成的矩阵为A(～)，证明：（A(～)）m＝E。

正确答案：
因为A^m=E,所以,A^m,=,A,^m=1,,A,=1≠0,即矩阵A可逆。
由题知A(~)=(A^*)^T,其中A^*为A的伴随矩阵。所以有(A(~))^m=[(A^*)^T]^m=[(,A,A^-¹)^T]^m=[(A^-¹)^T]^m=[(A^m)^-¹]^T=E。
解析：暂无解析
第11题：

问答题
设A为4阶魔术矩阵，分别对A进行如下操作：求矩阵A的逆；求矩阵A的行列式；求矩阵A的秩；求矩阵A的迹；

正确答案： >>A=magic（4）
>>B=inv（A）
>>C=det（A）
>>D=rank（A）
>>E=trace（A）
解析：暂无解析
第12题：

单选题
设有一个M*N的矩阵已经存放在一个M行N列的数组x中，且有以下程序段：sum=0;for(i=0;i
A
矩阵两条对角线元素之和
B
矩阵所有不靠边元素之和
C
矩阵所有元素之和
D
矩阵所有靠边元素之和

正确答案： A
解析：
程序执行过程为：第一个for循环实现对第一列和第N列求和。第二个for循环在上一个for循环结果上实现对第一行和第M行从第二个元素到第N-1个元素的求和，总体来说，就是矩阵所有靠边元素之和，答案选择D选项。
第13题：

已知矩阵.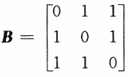，且矩阵X满足AXA+BXB=AXB+BXA+E，其中E是三阶单位矩阵，求X.

答案：
解析：
【解】化简矩阵方程，有AX(A-B)+BX(B-A)=E，即(A-B)X(A-B)=E.
由于，所以矩阵A-B可逆，且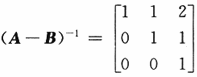于是.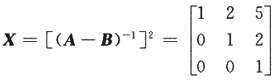
第14题：

设α为三维单位列向量，E为三阶单位矩阵，则矩阵E-αα^T的秩为________.

答案：
解析：
第15题：

初等矩阵（）

A.都可以经过初等变换化为单位矩阵
B.所对应的行列式的值都等于1
C.相乘仍为初等矩阵
D.相加仍为初等矩阵

答案：A
解析：
第16题：

设为3阶矩阵，将的第2列加到第1列得矩阵，再交换的第2行与第3行得单位矩阵，记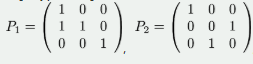，，则A=（）

答案：D
解析：
第17题：

与n阶单位矩阵E相似的矩阵是

A.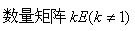
B.对角矩阵D（主对角元素不为1）
C.单位矩阵E
D.任意n阶矩阵A

答案：C
解析：
第18题：

设N阶矩阵A与对角矩阵合同,则A是().

A.可逆矩阵
B.实对称矩阵
C.正定矩阵
D.正交矩阵

答案：B
解析：
第19题：

阅读下列说明和C代码，回答问题1至问题3

【说明】某工程计算中要完成多个矩阵相乘（链乘）的计算任务。两个矩阵相乘要求第一个矩阵的列数等于第二个矩阵的行数，计算量主要由进行乘法运算的次数决定。采用标准的矩阵相乘算法，计算Am×n*Bn×p，需要m*n*p次乘法运算。矩阵相乘满足结合律，多个矩阵相乘，不同的计算顺序会产生不同的计算量。以矩阵A110×100，A2100×5，A35×50三个矩阵相乘为例，若按（A1*A2）*A3计算，则需要进行10*100*5+10*5*50=7500次乘法运算；若按A1*（A2*A3）计算，则需要进行100*5*50+10*100*50=75000次乘法运算。可见不同的计算顺序对计算量有很大的影响。矩阵链乘问题可描述为：给定n个矩阵

答案：
解析：
第20题：

可以产生由Z2上n阶线性常系数齐次递推关系式的矩阵A称为什么？（）
- A、乘方矩阵
- B、列矩阵
- C、单位矩阵
- D、生成矩阵
正确答案:D
第21题：

填空题
设n维向量α(→)＝（a，0，…，0，a）T，a＜0，E为n阶单位矩阵，矩阵A＝E－α(→)α(→)T，B＝E＋α(→)α(→)T/a，且B为A的逆矩阵，则a＝____。

正确答案： -1
解析：
由矩阵B是矩阵A的逆矩阵，所以有AB＝E。从而（E－α(→)α(→)^T）（E＋α(→)α(→)^T/a）＝E－α(→)α(→)^T＋α(→)α(→)^T/a－α(→)（α(→)^Tα(→)）α(→)^T/a＝E，即α(→)α(→)^T（1/a－1－2a²/a）＝0。
由于α(→)α(→)^T≠0，故1/a－1－2a²/a＝0，又因a＜0，可得a＝－1。
第22题：

单选题
设n维向量α(→)＝（a，0，…，0，a）T，a＜0，E为n阶单位矩阵，矩阵A＝E－α(→)α(→)T，B＝E＋α(→)α(→)T/a，且B为A的逆矩阵，则a＝（　　）。
A
4
B
2
C
－1
D
1

正确答案： B
解析：
由矩阵B是矩阵A的逆矩阵，所以有AB＝E。从而（E－α(→)α(→)^T）（E＋α(→)α(→)^T/a）＝E－α(→)α(→)^T＋α(→)α(→)^T/a－α(→)（α(→)^Tα(→)）α(→)^T/a＝E，即α(→)α(→)^T（1/a－1－2a²/a）＝0。
由于α(→)α(→)^T≠0，故1/a－1－2a²/a＝0，又因a＜0，可得a＝－1。
第23题：

单选题
可以产生由Z2上n阶线性常系数齐次递推关系式的矩阵A称为什么？（）
A
乘方矩阵
B
列矩阵
C
单位矩阵
D
生成矩阵

正确答案： D
解析：暂无解析

itgle.com

创建一个4阶魔术矩阵A与单位矩阵B，并分别计算两矩阵之和、矩阵相乘、矩阵点乘、A矩阵乘方、A矩阵装置。

题目

相似考题

更多“创建一个4阶魔术矩阵A与单位矩阵B，并分别计算两矩阵之和、矩阵相乘、矩阵点乘、A矩阵乘方、A矩阵装置。”相关问题

相关内容