itgle.com

单选题若8位二进制数能被4整除，则其最低2位（）。A 不可能是01、00B 只能是10C 可能是01、00D 只能是00

题目
单选题
若8位二进制数能被4整除，则其最低2位（）。
A

不可能是01、00

B

只能是10

C

可能是01、00

D

只能是00

相似考题

1.设三位数2a3加上326，得另一个三位数5b9，若5b9能被9整除，则a+b等于（ ）。A．2B．4C．6D．8

2.能被2整除的数叫做（ ），不能被2整除的数叫做（ ）。

3.若将有限状态自动机(DFA)识别的0、1符号串看做二进制数，则自动机(27)识别的是能被十进制数3整除的正整数。A．B．C．D．

4.● 若8位二进制数能被4整除，则其最低2位 （1） 。（1）A. 不可能是01、00B. 只能是10C. 可能是01、00D. 只能是00

更多“若8位二进制数能被4整除，则其最低2位（）。”相关问题

  • 第1题：

    从1，2，3，4，…，2007中取N个不同的数，其中任意三个数的和能被15整除。则N最大为（ ）。

    A．134

    B．267

    C．316

    D．133


    正确答案：A
    取出的N个不同的数，任意三个的和都能被15整除，分两种情况：
    (1)这N个数都能被15整除
    在1—2007中，能被15整除的数为15×1，15×2，…，15×133，共有133个。
    (2)这N个数除以15的余数都为5
    在1—2007中，能被15除余5的数为15×0＋5，15×1＋5，…，15×133＋5，共有134个。故N最大为134。

  • 第2题：

    从1.2，3，4，…，2007中取N个不同的数，其中任意三个数的和能被15整除。则N最大为()。

    A．134

    B．267

    C．316

    D．133


    正确答案：A

  • 第3题：

    设三位数2a3加上326，得另一个三位数5b9，若5b9能被9整除，则a+b等于（ ）。

    A. 2

    B. 4

    C. 6

    D. 8


    正确答案：C

    由2a3+326=5b9可得，a+2=b，又5b9能被9整除，可知b=4，则a=2，所以a+b=2+4=6。

  • 第4题：

    若将有限状态自动机(DFA)识别的0、1符号串看作二进制数，则(6)识别的是能被十进制数3整除的正整数，(7)是与该自动机等价的正规式。

    A．

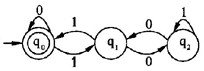
    B．

    C．

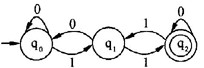
    D．


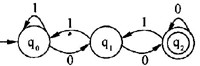    正确答案：A
    解析：任何一个整数被3除后，余数或为0、或为1、或为2。因此，若将该DFA识别的0、 1串看作是二进制整数，则有以下结论：
      ▲ 0被3除，余数为0。
      ▲ 设能被3整除的二进制数为x。若在x之后连接一个0所得的数为y，则y=2x，且y被3整除的余数仍然为0。若在x之后连接一个1所得的数为y，则y=2x+1，因此， y被3整除的余数将等于1。
      ▲ 设被3整除后余数为1的二进制数为x。若在x之后连接一个0所得的数为y，则y=2x，且y被3整除的余数为2。若在x之后连接一个1所得的数为y，则y2x+l，且y被3整除的余数将等于0。  ‘
      ▲ 设被3整除后余数为2的二进制数为x。若在x之后连接一个0所得的数为y，则y=2x，且y被3整除的余数为1。若在x之后连接一个1所得的数为y，则y=2x+l，且y被3整除的余数仍等于2。
      综上，设被3除后的余数为0用qo(下标)表示、余数为1用q1(下标)表示、余数为2用q2(下标)表示，若将空串的值看作0，则下图所示的自动机识别的是能被3整除的整数，其正规式为(0* (1(01*0)*1)*)*。
     
      若限定该自动机识别的0、1序列不能为空串，则相应自动机的状态转换图如下图所示。
     

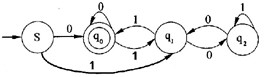
  • 第5题：

    编程求出个位数字是4且能被7整除的所有3位数之和。


    答案：
    解析：



  • 第6题：

    若x2+x3+ax+b能被x2-3x+2整除，则（ ）

    A.a=4 b=4
    B.a=-4,b=-4.
    C.a=10,b=-8
    D.a=-10,b=8
    E.a=-2,b=0

    答案：D
    解析：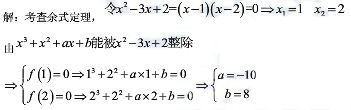

  • 第7题：

    若8位二进制数能被4整除，则其最低2位（）。

    • A、不可能是01、00
    • B、只能是10
    • C、可能是01、00
    • D、只能是00

    正确答案:D

  • 第8题：

    下列推理是什么类型的？写出它的推理形式，并说明其是否有效的理由。  （1）如果一部作品是优秀的，它一定如实反映了生活，这部作品如实反映了生活，所以，它是优秀的。  （2）只有能被2整除的数，才能被4整除，8是能被2整除的数，所以，8是能被4整除的数。  （3）一个结论假的演绎推理或是前提假或是推理形式无效，这个结论假的演绎推理是前提假的，所以，它不是推理形式无效的。


    正确答案: （1）充分条件假言推理。推理形式为：“如果A那么B，B，所以，A。”该推理形式无效，小前提与假言前提构成肯定后件式，违反了“肯定后件不能肯定前件”的规则。
    （2）必要条件假言推理。推理形式为：“只有A才B，A，所以，B。”该推理形式无效，小前提与假言前提构成肯定前件式，违反了“肯定前件不能肯定后件”的规则。
    （3）选言推理。推理形式为：“或者A或者B，A，所以，非B。”该推理形式无效，小前提与选言前提构成肯定否定式，违反了相容选言推理“肯定一个肢，不能否定另一肢”的规则。

  • 第9题：

    将条件“y能被4整除但不能被100整除，或y能被400整除”写成逻辑表达式（）。


    正确答案:y%4==0&&y%100!=0||y%400==0

  • 第10题：

    单选题
    一个数能被3，5，7整除，若用11去除这个数则余1，这个数最小是多少？（　　）
    A

    105

    B

    210

    C

    265

    D

    375


    正确答案： B
    解析：
    由“能被3，5，7整除”可知，这个数为105n（n为正整数），又“用11去除这个数则余1”，当n＝2时，105×2＝210，且210÷11＝19……1，即这个数最小为210。

  • 第11题：

    单选题
    判断年份是否为闰年，如果是，结果保存“闰年”，如果不是，则结果保存“平年”，说明：闰年定义：年数能被4整除而不能被100整除，或者能被400整除的年份。使用哪个函数？，（）
    A

    IF

    B

    COUNTF

    C

    RANK

    D

    COUNTA


    正确答案： C
    解析： 暂无解析

  • 第12题：

    单选题
    从1，2，3，4，…，2007中取N个不同的数，其中任意三个数的和能被15整除。则N最大为（　　）。
    A

    134

    B

    267

    C

    316

    D

    133


    正确答案： D
    解析：
    取出的N个不同的数，任意三个的和都能被15整除，分三种情况：①这N个数都能被15整除，在1～2007中，能被15整除的数为15×1，15×2，…，15×133，共133个；②这N个数除以15的余数都为，在1～2007中，能被15除余5的数为15×0＋5，15×1＋5，…，15×133＋5，共有134个；②这N个数除以15的余数都为10，在1～2007中，能被15除余10的数的个数为15×0＋10，15×1＋10，…，15×133＋10，共有134个。则N最大为134。

  • 第13题：

    若8位二进制数能被4整除，则其最低2位(1)。

    A．不可能是01、00

    B．只能是10

    C．可能是01、00

    D．只能是00


    正确答案：D
    解析：本题考查计算机系统数据表示基础知识。从十进制数的观点来看，能被4整除的数是4的倍数，例如，5、8、12…，这些数表示为二进制形式时，为00000100、00001000、00001100…，在这些数的基础上每次加上4就得到4的倍数，显然这些二进制数的最低2位一定是00。

  • 第14题：

    用数字4、5、6、7、8、9这六个数字组成一个六位数ABCDEF(不一定按给出数字的顺序排列)，若把A移到最后，所得的六位数BCDEFA能被2整除，若再把8移到最后，所得的六位数CDEFAB能被3整除，…，依此类推，若把E移到最后，所得的六位数能被6整除，则六位数ABCDEF的最小值为（ ）。

    A．476598

    B．476589

    C．456789

    D．465879


    正确答案：B
    此题可用排除法，因为把D移到最后，可以被5整除，所以D一定为5，排除C、D；若要保证能被2、4、6整除，所以A、C、E必须是偶数，排除A，故选B。

  • 第15题：

    六位数442738，能被72整除，且这六个数之和能被9整除，A与B的值为（ ）。

    A．6，5

    B．5，6

    C．7，0

    D．6，2


    正确答案：B
    72—8×9，因此六位数A42738能被8与9整除，所以后三位738能被8整除，故B=6。又由于A+4+2+7+3+B能被9整除，结合选项所以A=5。

  • 第16题：

    1～200这200个自然数中，能被4或能被6整除的数有多少个？( )


    A. 65
    B. 66
    C. 67
    D. 68

    答案：C
    解析：
    能被4整除的有[200/4]＝50个能被6整除的有[200/6]＝33个注：[]表示取整而两者却重复计算了同时能被4和6整除的数，所以需要减去能被4，6共同整除的有[200/12]＝16个于是能被4或能被6整除的数50+33-16＝67个

  • 第17题：

    考生若考试通过并且体检合格，则将被录取。因此，如果李铭考试通过，但未被录取，那么他一定体检不合格。以下哪项与上述论证方式最为相似？

    A.若明天是节假日并且天气晴朗，则小吴将去爬山。因此，如果小吴未去爬山，那么第二天一定不是节假日或者天气不好。
    B.一个数若能被3整除且能被5整除，则这个数能被15整除。因此这一个数若能被3整除但不能被5整除，则这个数一定不能被15整除。
    C.甲单位员工若去广州出差并且是单人前往，则均乘坐高铁。因此，甲单位小吴如果去广州出差，但未乘坐高铁，那么他一定不是单人前往。
    D.若现在是春天并且雨水充沛，则这里野草丰美。因此，如果这里野草丰美，但雨水不充沛，那么现在一定不是春天。
    E.一壶茶若水质良好且温度适中，则一定茶香四溢。因此，如果这壶茶水质良好且茶香四溢，那么一定温度适中。

    答案：C
    解析：
    【C】解析：形式逻辑，平行结构，相似。题干：考生若考试通过并且体检合格，则将被录取。因此，如果李铭考试通过，但未被录取，那么他一定体检不合格。其逻辑结构：A且B→C。因此，A且非C→非B。C和题干结构一致。

  • 第18题：

    充分条件指的是对于两个命题X和Y，当X成立时，则Y成立，那么X是Y的充分条件；必要要条件指的是对于两个命题X和Y，当X不成立时，则Y不成立，那么X是Y的必要条件。
    根据上述定义，下列哪项中X是Y的必要条件？

    A.X：该数能被6整除；Y：该数能被2整除
    B.X：该数能被6整除；Y：该数能被4整除
    C.X：该数能被3整除；Y：该数能被6整除
    D.X：该数能被4整除；Y：该数能被3整除

    答案：C
    解析：
    本题考查“必要条件”的定义。
    其关键信息为：当X不成立时，则Y不成立。
    A项，当一个数不能被6整除时，无法得到该数不能被2整除，比如“4”，不符合定义，故A项错误，排除。
    B项，当一个数不能被6整除时，无法得到该数不能被4整除，比如“4”，不符合定义，故B项错误，排除。
    C项，因为6可以被分解为2×3，所以不能被3整除，就一定就不能被6整除，符合定义，故C项正确，当选。
    D项，当一个数不能被4整除时，无法得到该数不能被3整除，比如“6”，不符合定义，故D项错误，排除。
    故本题的正确答案为C项。

  • 第19题：

    三段论：“因为3258的各位数字之和能被3整除，所以3258能被3整除”。前提是（）

    • A、 “3258能被3整除”是小前提
    • B、 “3258的各位数字之和能被3整除”是大前提
    • C、 “各位数字之和能被3整除的数都能被3整除” 是省略的大前提
    • D、 “3258能被3整除”是大前提

    正确答案:C

  • 第20题：

    偶数是能被2整除的数，所以 所有能被2整除的数是偶数。


    正确答案:错误

  • 第21题：

    闰年的条件是年号（year）能被4整除，但不能被100整除，或者能被400整除。则闰年的布尔表达式为（）。

    • A、（yearmod4=0andyearmod100<>0）and（yearmod400=0）
    • B、（yearmod4=0andyearmod100<>0）or（yearmod400=0）
    • C、（yearmod4=0oryearmod100<>0）and（yearmod400=0）
    • D、（yearmod4=0oryearmod100<>0）or（yearmod400=0）

    正确答案:B

  • 第22题：

    判断题
    偶数是能被2整除的数，所以 所有能被2整除的数是偶数。
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

  • 第23题：

    单选题
    三段论：“因为3258的各位数字之和能被3整除，所以3258能被3整除”。前提是（）
    A

     “3258能被3整除”是小前提

    B

     “3258的各位数字之和能被3整除”是大前提

    C

     “各位数字之和能被3整除的数都能被3整除” 是省略的大前提

    D

     “3258能被3整除”是大前提


    正确答案： C
    解析： 暂无解析

  • 第24题：

    单选题
    闰年的条件是年号（year）能被4整除，但不能被100整除，或者能被400整除。则闰年的布尔表达式为（）。
    A

    （yearmod4=0andyearmod100<>0）and（yearmod400=0）

    B

    （yearmod4=0andyearmod100<>0）or（yearmod400=0）

    C

    （yearmod4=0oryearmod100<>0）and（yearmod400=0）

    D

    （yearmod4=0oryearmod100<>0）or（yearmod400=0）


    正确答案： C
    解析： 暂无解析

相关内容