itgle.com

单选题已知直线，mx＋4y－2＝0与2x－5y＋n＝0互相垂直，垂足为（1，P），则m－n＋P的值为（　　）A 24B 20C 0D －4

题目
单选题
已知直线，mx＋4y－2＝0与2x－5y＋n＝0互相垂直，垂足为（1，P），则m－n＋P的值为（　　）
A

24

B

20

C

0

D

－4

相似考题

1.已知“inta[]={1,2,3};constint*p=a;”,则语句“*p=5;”会将元素a[0]的值赋为5.()此题为判断题(对，错)。

2.设平面方程为x+y+z+1=0，直线方程为1－x=y+1=z，则直线与平面： A.平行 B.垂直 C.重合 D.相交但不垂直

3.已知直线L1过点M1(0，0，-1)且平行于X轴，L2过点M2(0，0，1)且垂直于XOZ平面，则到两直线等距离点的轨迹方程为( )。A. B. C. D.

4.已知“int a=1,b=2,c=3,x;”与“x=(a^b)&c;”,则x的值为()A.0B.1C.2D.3

更多“已知直线，mx＋4y－2＝0与2x－5y＋n＝0互相垂直，垂足为（1，P），则m－n＋P的值为（　　）”相关问题

  • 第1题：

    已知某瞬时平面图形上O点的加速度为a0。图形的角速度ω=0，角加速度为α0。则图形上过O点并垂直于a0的直线mn上各点加速度的方向应是( )。


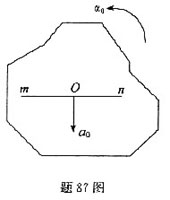    A.指向O点
    B.垂直mn直线
    C.与mn直线成θ角
    D.沿mn直线背离O点

    答案：B
    解析：
    用基点法求加速度

  • 第2题：

    已知平面π过点(1，1，0)、(0，0，1)、(0，1，1)，则与平面π垂直且过点(1，1，1)的直线的对称方程为 ( )。



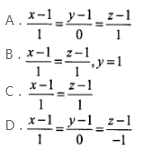    答案：B
    解析：
    平面π的法向量所求直线的方向向量为i+k，故应选B。@##

  • 第3题：

    设曲线y=^e1?x2与直线x=-1的交点为P，则曲线在点P处的切线方程是（　　）

    A．2x-y+2=0
    B．2x+y+1=0
    C．2x+y-3=0
    D．2x-y+3=0

    答案：D
    解析：


    @##

  • 第4题：

    若直线ax+y+5=0，与直线x-2y+7=0垂直，则a的值为______ 。


    答案：
    解析：
    两直线垂直时，斜率之积为-1。计算可得a=2。

  • 第5题：

    已知平面π过点M1(1，1，0)，M2(0，0，1)，M3(0，1，1)，则与平面π垂直且过点(1，1，1)的直线的对称方程为：



    答案：A
    解析：
    提示 求出过M1，M2，M3三点平面的法线向量。



    @##

  • 第6题：

    设直线的方程为x=y-1=z， 平面的方程为x-2y+z=0，则直线与平面（ ）。
    A.重合 B.平行不重合 C.垂直相交 D.相交不垂直


    答案：B
    解析：
    正确答案为B。
    提示：直线的方向向量为s = (1，1，1)，平面的法向量为n= (1，-2，1)，s·n = 1-2 + 1 = 0,这两个向量垂直，直线与平面平行，又直线上的点(0，1，0)不在平面上，故直线与平面不重合。

  • 第7题：

    已知抛物线y2=2px(p>0)，过定点(p，0)作两条互相垂直的直线l1、l2，l1与抛物线交于


    答案：
    解析：
    (pk2+P，-pk)

  • 第8题：

    已知P{X≤0，Y≤0}=1/3，P{X>0}=1/2，P{Y>0}=1/3，则P{min（X，Y）≤0}=（）


    正确答案:5/6

  • 第9题：

    单选题
    已知点P（a2－1，2a＋1）在直线x－2y－2＝0上，则a的值是（　　）．
    A

    5

    B

    －1

    C

    5或－1

    D

    －5或1


    正确答案： A
    解析：
    将点P的坐标代入直线方程得a＝5或－1．

  • 第10题：

    单选题
    设集合M＝{直线}，P＝{圆}，则集合M∩P中的元素个数为（　　）。
    A

    0

    B

    1

    C

    2

    D

    0或1或2


    正确答案： B
    解析：
    因为不存在既是直线又是圆的图形，所以M∩P是空集。

  • 第11题：

    单选题
    设直线的方程为x=y-1=z，平面的方程为x-2y+z=0,则直线与平面（ ）
    A

    重合

    B

    平行不重合

    C

    垂直相交

    D

    相交不垂直


    正确答案： C
    解析：

  • 第12题：

    单选题
    三个偏振片P1、P2与P3堆叠在一起，P1与P3的偏振化方向相互垂直，P2与P1的偏振化方向间的夹角为30°。强度为I0的自然光垂直入射于偏振片P1，并依次透过P1、P2与P3，则通过三个偏振片后的光强为（）。
    A

    I0/4

    B

    3I0/8

    C

    3I0/32

    D

    I0/16


    正确答案： A
    解析： 暂无解析

  • 第13题：

    设直线方程为x=y-1=z，平面方程为x-2y+z=0，则直线与平面：
    A.重合 B.平行不重合
    C.垂直相交 D.相交不垂直


    答案：B
    解析：
    从而知直线//平面或直线与平面重合；再在直线上取一点（0,1,0），验证该点是否满足平面方程。

  • 第14题：

    如果函数f(x)=在x=0处连续，则p、q的值为:
    A.p=0,q=0 B.p=0,q=1 C.p=1,q=0 D.p=1,q=1


    答案：D
    解析：
    提示：利用函数在x=0点连续的定义f(x+0)=f(x-0)=f(0)，求p、q值。


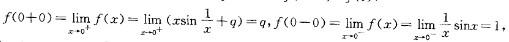
    f(0)=p，求出 p=q=1。

  • 第15题：

    如图所示。直线AB与DF相交于点0，OD平分∠BOC，EO⊥D0，垂足为0，则∠COF与∠BOE的差为()。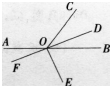

    A.30o
    B.45o
    C.60o
    D.90o

    答案：D
    解析：
    ∠COF+∠COD=180°，∠BOE+∠BOD=90°，且∠COD=∠BOD，两式相减可知∠COF- ∠BOE=90°。

  • 第16题：

    已知 a2+a+1=0，则 a2008+a2009+1的值为（）。

    A.0
    B.1
    C.2
    D.3

    答案：A
    解析：
    由a2+a+1=0，联想到逆用立方差公式，求出a3的值，进而通过转化求代数式的值。
    如果 a=1，那么 a2+a+1=1+1+1=3≠0，即 a≠1。
    等式两边同乘以a-1，得到(a-1)(a2+a+1)=a3-1=0，即a3=1。

    因为2007能整除3，所以a2007=1。
    a2008+a2009+1=a2007(a2+a)+1=a2+a+1=0。

  • 第17题：

    若f(x)为可导函数，且已知f(0) = 0，f'(0) = 2,则的值为()。
    A. 0 B. 1 C. 2 D.不存在


    答案：B
    解析：
    提示：利用积分上限函数求导和洛必达法则。

  • 第18题：

    已知平面π过点(1,1，0)、(0,0,1), (0,1,1),则与平面π垂直且过点(1,1,1)的直线的对称式方程为（ ）。


    答案：B
    解析：
    正确答案是B。
    提示：平面π的法向量，所求直线的方向向量为i+k ,故应选B。

  • 第19题：

    已知直线经过（x1，y1）点，斜率为k(k≠0)，则直线方程为y=2kx+2。


    正确答案:错误

  • 第20题：

    设直线的方程为x=y-1=z，平面的方程为x-2y+z=0，则直线与平面（）。

    • A、重合
    • B、平行不重合
    • C、垂直相交
    • D、相交不垂直

    正确答案:B

  • 第21题：

    填空题
    直线（3a＋2）x＋（1－4a）y＋8＝0与（5a－2）x＋（a＋4）y－7＝0互相垂直，则a的值为____.

    正确答案： 0或1
    解析：
    根据两条直线垂直的充要条件，有（3a＋2）（5a－2）＋（1－4a）（a＋4）＝0，解方程得：a＝0或a＝1．

  • 第22题：

    单选题
    三个偏振片P1、P2与P3堆叠在一起，P1与P3的偏振化方向相互垂直，P2与P1的偏振化方向间的夹角为30°。强度为I0的自然光垂直入射于偏振片P1，并依次透过偏振片P1、P2与P3，则通过三个偏振片后的光强为：（）
    A

    I0／4

    B

    3I0／8

    C

    3I0／32

    D

    I0／16


    正确答案： C
    解析： 暂无解析

  • 第23题：

    单选题
    已知直线，mx＋4y－2＝0与2x－5y＋n＝0互相垂直，垂足为（1，P），则m—n＋P的值为（　　）
    A

    24

    B

    20

    C

    0

    D

    －4


    正确答案： B
    解析：
    由两直线垂直的斜率关系可得m＝10，直线方程为5x＋2y－1＝0和2x－5y＋n＝0，当x＝1时，y＝－2，即P＝－2，将交点代入2x－5y＋n＝0得n＝－12，因此m—n＋P＝20．

相关内容