itgle.com

设平面方程为x+y+z+1=0，直线方程为1－x=y+1=z，则直线与平面： A.平行 B.垂直 C.重合 D.相交但不垂直

题目
设平面方程为x+y+z+1=0，直线方程为1－x=y+1=z，则直线与平面：

A.平行
B.垂直
C.重合
D.相交但不垂直
相似考题

1.设平面方程x+y+Z+1=0，直线的方程是l-x=y+1= z，则直线与平面： (A)平行 （B)垂直 (C)重合 (L)相交但不垂直

2.设直线方程为x=y-1=z，平面方程为x-2y+z=0，则直线与平面： A.重合 B.平行不重合 C.垂直相交 D.相交不垂直

3.设平面方程:x + y + z-1 = 0，直线的方程是1-x = y + 1=z，则直线与平面： A.平行 B.垂直 C.重合 D.相交但不垂直

4.平面3x-2y+z+3=0与平面x+5y+7z-1=0的位置关系()。A.平行 B.垂直 C.相交且不垂直 D.重合

参考答案和解析
答案：D
解析：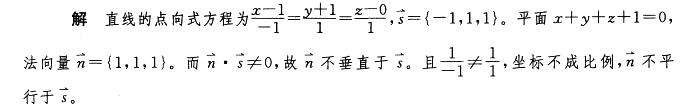
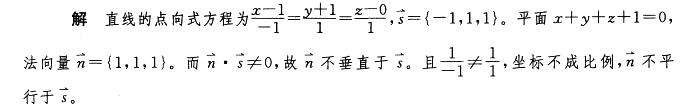
更多“设平面方程为x+y+z+1=0，直线方程为1－x=y+1=z，则直线与平面： A.平行 B.垂直 C.重合 D.相交但不垂直”相关问题

  • 第1题：

    设平面方程为x+y+z+1=0，直线方程为1－x=y+1=z，则直线与平面：

    A.平行
    B.垂直
    C.重合
    D.相交但不垂直

    答案：D
    解析：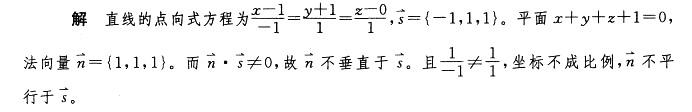

  • 第2题：

    下列平面中，平行于且与yOz坐标面非重合的平面方程是（　　）。

    A． y＋z＋1＝0
    B． z＋1＝0
    C． y＋1＝0
    D． x＋1＝0

    答案：D
    解析：
    D项，平面方程x＋1＝0化简为x＝－1，显然平行yOz坐标面，且不重合。ABC三项，均与yOz坐标面重合。

  • 第3题：

    直线L：2x=5y=z-1与平面∏：4x-2z=5的位置关系是( ).

    A.直线L与平面∏平行
    B.直线L与平面∏垂直
    C.直线L在平面∏上
    D.直线L与平面∏相交，但不垂直

    答案：A
    解析：
    直线L的方程可改写为x/(5/2)=y/1=(z-1)/5由此可得直线L的方向向量s=(5/2，1，5).平面∏的法向量n=(4，0，-2).s·n=4·5/2+0-2·5=0，故直线与平面平行或直线在平面上.又L上一点(0，0，1)不在平面∏上，故选A.

  • 第4题：

    设平面π的方程为2x－2y+3=0，以下选项中错误的是( )。

    A.平面π的法向量为i-j
    B.平面π垂直于z轴
    C.平面π平行于z轴
    D.

    答案：B
    解析：

  • 第5题：

    直线 与平面π：x+y+z=2的位置关系

    A、平行
    B、相交但不垂直
    C、垂直
    D、直线f在平面上

    答案：B
    解析：
    由题意得：直线L的方向向量为m=(2，一l，一3)，平面霄的法向量即=(1，1，1)，易知m与，l不共线，且m·n#0，而直线l上的点(1，一l，2)在平面π上，故两者相交但不垂直。故选择B。

  • 第6题：

    设直线的方程为x=y-1=z， 平面的方程为x-2y+z=0，则直线与平面（ ）。
    A.重合 B.平行不重合 C.垂直相交 D.相交不垂直


    答案：B
    解析：
    正确答案为B。
    提示：直线的方向向量为s = (1，1，1)，平面的法向量为n= (1，-2，1)，s·n = 1-2 + 1 = 0,这两个向量垂直，直线与平面平行，又直线上的点(0，1，0)不在平面上，故直线与平面不重合。

  • 第7题：

    设直线的方程为x=y-1=z，平面的方程为x-2y+z=0，则直线与平面（）。

    • A、重合
    • B、平行不重合
    • C、垂直相交
    • D、相交不垂直

    正确答案:B

  • 第8题：

    直线L1：2x=5y=z-1与平面∏：4x-2z=5的位置关系是（）．

    • A、直线L与平面∏平行
    • B、直线L与平面∏垂直
    • C、直线L在平面∏上
    • D、直线L与平面∏相交，但不垂直

    正确答案:A

  • 第9题：

    单选题
    设直线方程为x=y-1=z，平面方程为x-2y+z=0，则直线与平面（　　）。[2011年真题]
    A

    重合

    B

    平行不重合

    C

    垂直相交

    D

    相交不垂直


    正确答案： A
    解析：
    直线的方向向量s＝（1，1，1），平面的法向向量n＝（1，－2，1），其向量积s·n＝1－2＋1＝0，则这两个向量垂直，即直线与平面平行。又该直线上的点（0，1，0）不在平面上，故直线与平面不重合。

  • 第10题：

    单选题
    设直线的方程为x=y-1=z，平面的方程为x-2y+z=0，则直线与平面（）。
    A

    重合

    B

    平行不重合

    C

    垂直相交

    D

    相交不垂直


    正确答案： B
    解析： 暂无解析

  • 第11题：

    设平面π的方程为2x-2y+3 = 0，以下选项中错误的是：
    A.平面π的法向量为i-j
    B.平面Π垂直于z轴
    C.平面Π平行于z轴



    答案：B
    解析：


    @##

  • 第12题：

    设平面π的方程为x+z-3=0，以下选项中错误的是( )。

    A.平面π垂直于zox面
    B.平面π垂直于y轴
    C.平面π的法向量为i+k
    D.平面π平行于y轴

    答案：B
    解析：

  • 第13题：


    A.平行，但直线不在平面上
    B.直线在平面上
    C.垂直相交
    D.相交但不垂直

    答案：A
    解析：
    直线方向向量与平面法向量垂直，且直线上点不在平面内。

  • 第14题：


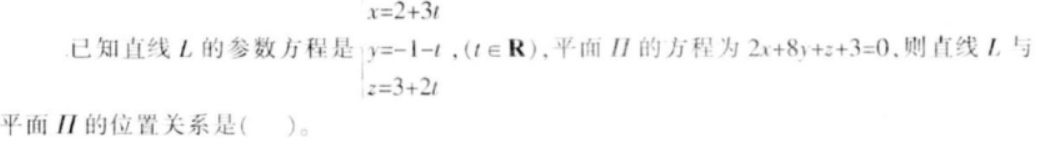    A.平行
    B.直线在平面内
    C.垂直
    D.相交但不垂直

    答案：A
    解析：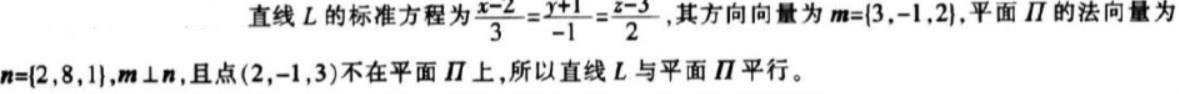

  • 第15题：


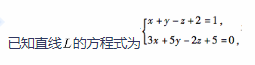
    平面Ⅱ的方程为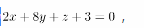

    则直线 与平面Ⅱ的位置关系是( )。


    A.平行
    B.直线在平面内
    C.垂直
    D.相交但不垂直

    答案：A
    解析：
    本题主要考查直线与平面的位置关系的判定。

  • 第16题：

    设平面π1：2x+y+4z+4=0,π2：2x-8y+z+1=0,则平面π1与π2的位置关系是（）

    A.相交且垂直
    B.相交但不垂直
    C.平行但不重合
    D.重合

    答案：A
    解析：
    平面π1的法线向量，n1=(2，1，4)，平面π2的法线向量n2=(2，-8，1)，n1·n2=0．可知两平面垂直，因此选A．

  • 第17题：

    直线L：2x=5y=z-1与平面∏：4x-2z=5的位置关系是（）.

    • A、直线L与平面∏平行
    • B、直线L与平面∏垂直
    • C、直线L在平面∏上
    • D、直线L与平面∏相交，但不垂直

    正确答案:A

  • 第18题：

    单选题
    直线L：（x＋3）/（－2）＝（y＋4）/（－7）＝z/3与平面∏：4x－2y－2z＝3的关系是（　　）。
    A

    平行

    B

    直线L在平面∏上

    C

    垂直相交

    D

    相交但不垂直


    正确答案： B
    解析：
    平面∏：4x－2y－2z＝3的法向量为n(→)＝{2，－1，－1}，直线L：（x＋3）/（－2）＝（y＋4）/（－7）＝z/3的方向向量l(→)＝{－2，－7，3}，由于l(→)·n(→)＝（－2）×2＋（－7）×（－1）＋3×（－1）＝0，所以直线与平面平行。

  • 第19题：

    单选题
    直线L1：2x=5y=z-1与平面∏：4x-2z=5的位置关系是（）．
    A

    直线L与平面∏平行

    B

    直线L与平面∏垂直

    C

    直线L在平面∏上

    D

    直线L与平面∏相交，但不垂直


    正确答案： C
    解析： 暂无解析

  • 第20题：

    单选题
    已知直线L：x/3＝（y＋1）/（－1）＝（z－3）/2，平面π：－2x＋2y＋z－1＝0，则（　　）。[2013年真题]
    A

    L与π垂直相交

    B

    L平行于π但L不在π上

    C

    L与π非垂直相交

    D

    L在π上


    正确答案： D
    解析：
    直线L的方向向量为±（3，－1，2），平面π的法向量为（－2，2，1），由于3/（－2）≠（－1）/2≠2/1，故直线与平面不垂直；又3×（－2）＋（－1）×2＋2×1＝－6≠0，所以直线与平面不平行。所以直线与平面非垂直相交。直线L与平面π的交点为（0，－1，3）。

相关内容