itgle.com

已知点A（-4，2），B（0，o），则线段AB的垂直平分线的斜率为 （ ）A.AB.BC.CD.D

题目

已知点A（-4，2），B（0，o），则线段AB的垂直平分线的斜率为 （ ）

A.A

B.B

C.C

D.D

相似考题

1.已知过点（0，4），斜率为-1的直线l与抛物线C：y2—2px（b&gt；0）交于A，B两点．（I）求C的顶点到2的距离；（Ⅱ）若线段AB中点的横坐标为6，求C的焦点坐标．

2.函数y=x²＋x－2,已知该曲线在点M处的切线斜率为3,则点M的坐标是(2,0)。()此题为判断题(对，错)。

3.已知起航点经度，到达点经度，则两地间的经差Dλ为：A.AB.BC.CD.D

4.已知圆22+y2+4x-8y+11=0，经过点P（1，o）作该圆的切线，切点为Q，则线段PQ的长为 （ ）A.10B.4C.16D.8

更多“已知点A（-4，2），B（0，o），则线段AB的垂直平分线的斜率为 （ ）A.AB.BC.CD.D”相关问题

  • 第1题：

    已知测者经度λ＝27°42.′0W所在时区的区时ZT＝（2月11日），则该地的地方平时LMT＝________。

    A.A

    B.B

    C.C

    D.D


    正确答案：A

  • 第2题：

    已知点A的坐标为(2,－1),AB=4,AB∥X轴,则B点的坐标为_________


    正确答案：
     (－2，－1)，（6，－1） 

  • 第3题：

    先将线段AB分成20等分，线段上的等分点用“△”标注，再将该线段分成21等分，等分点用“O”标注（AB两点都不标注），现在发现“△”和“O”之间的最短处2厘米，问线段AB的长度为多少？


    A. 2460
    B. 1050
    C. 840
    D. 680

    答案：C
    解析：
    解题指导： 20和21的公倍数是420。所以AB长度为420*2=840厘米。故答案为C。

  • 第4题：

    已知某瞬时平面图形上O点的加速度为a0。图形的角速度ω=0，角加速度为α0。则图形上过O点并垂直于a0的直线mn上各点加速度的方向应是( )。


    A.指向O点
    B.垂直mn直线
    C.与mn直线成θ角
    D.沿mn直线背离O点

    答案：B
    解析：
    用基点法求加速度

  • 第5题：

    已知A(-1，-l)，B(3，7)两点，则线段AB的垂直平分线方程为__________.


    答案：
    解析：
    【答案】χ+2y=0 【考情点拨】本题主要考查的知识点为线段的垂直平分线．
    【应试指导】设线段的垂直平分线上任一点为P(χ，y)，则
    即

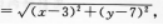
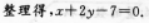
  • 第6题：

    已知三点A（1,-2）,B（m,2）,且线段AB的垂直平分线的方程是x+2y-2=0,则实数m的值为（ ）

    A.-2
    B.-7
    C.3
    D.1
    E.2

    答案：C
    解析：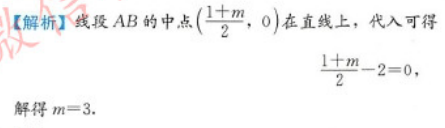

  • 第7题：

    C是线段AB上一点，D是线段CB的中点，已知图中所有线段的长度之和为23，线段 AC和线段CB的长度都是正整数,那么线段4C的长度为：



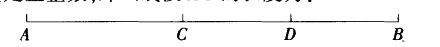    A.2
    B.3
    C.5
    D.7

    答案：B
    解析：
    。解析是Cfl的中点’CD=DB=1/2CB。所有线段长度之和=4C+AD+AB+CD+CB+DB=AC+(AC+

  • 第8题：

    已知线段AB的方位角为160°，则线段BA的方位角为（）。

    • A、-120°
    • B、340°
    • C、160°
    • D、20°

    正确答案:B

  • 第9题：

    已知直线经过（x1，y1）点，斜率为k(k≠0)，则直线方程为y=2kx+2。


    正确答案:错误

  • 第10题：

    已知A点坐标为（1000，1000），B点坐标为（543.245，1000），则直线AB的方位角为（）

    • A、0º00ˊ00″
    • B、180º00ˊ00″
    • C、90º00ˊ00″

    正确答案:A

  • 第11题：

    单选题
    已知线段AB的两端点坐标，可计算tgαAB=△y/△x，R＝arctg△y/△x，R>0，若使αAB＝R＋180则（）。
    A

    △x＞0，△y>0

    B

    △x<0，△y>0

    C

    △x<0，△y<0

    D

    △x＞0，△y<0


    正确答案： B
    解析： 暂无解析

  • 第12题：

    单选题
    已知线段AB的方位角为160°，则线段BA的方位角为（）。
    A

    -120°

    B

    340°

    C

    160°

    D

    20°


    正确答案： A
    解析： 暂无解析

  • 第13题：

    已知平面向量a=（1，1），b=（1，-l），则两向量的夹角为（ ）

    A.A

    B.B

    C.C

    D.D


    正确答案：C
    本题主要考查的知识点为向量的数量积的性质．【应试指导】

  • 第14题：

    如右图，已知直线AB是⊙O的切线，A为切点，OB交⊙O于点C，点D在⊙0上，且∠OBA=40°，则∠ADC=_______．



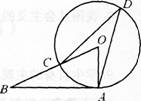    答案：
    解析：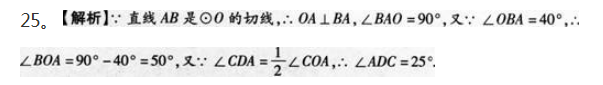

  • 第15题：

    先将线段AB分成20等分，线段上的等分点用"A"标注，再将该线段分成21等分，等分点 用“O”标注（AB两点都不标注），现在发现"A"和“O”之间的最短处为2厘米，问线段AB 的长度为多少？（ ）
    A. 2460厘米 B. 1050厘米
    C. 840厘米 D. 680厘米


    答案：C
    解析：
    不妨设线段AB长度为x，且从左端开始计算距离。先将线段AB分成20等分，线段上的等分点用“A’’标注，则每个“A"的位置为nx/20， 且 l n 19;再将该线段分成21等分，等分点用“O"标注，则每个“O"的位置为kx/21， 且 l k 20;nx/20— kx/21 = x(21n—20k)/420，则显然当 n = k=l 时候，此式值最小。 因为“A’’和“O”之间的最短处为2厘米，即x/420 = 2，解得x=840厘米。

  • 第16题：

    已知χ轴上的一点B与点A(5，12)的距离等于13，则点B的坐标为( )

    A.(10，0)
    B.(0，0)
    C.(10，O)或(0，0)
    D.(-10，0)

    答案：C
    解析：
    【考情点拨】本题主要考查的知识点为两点间距 离公式．
    【应试指导】设B(χ，0)，由两点间的距离公
    式得：

  • 第17题：

    A．B是抛物线y2=8x上两点，且此抛物线的焦点在线段AB上，已知A．B两点的横坐标之和为10，则|AB|=（　　）

    A.18
    B.14
    C.12
    D.10

    答案：B
    解析：

  • 第18题：

    设A,B皆为n阶矩阵,则下列结论正确的是().

    A.AB=O的充分必要条件是A=O或B-O
    B.AB≠O的充分必要条件是A≠0且B≠0
    C.AB=O且r(A)=N,则B=O
    D.若AB≠0,则｜A｜≠0或｜B｜≠0

    答案：C
    解析：

  • 第19题：

    已知圆O的方程为x2+y2=1，过点P(-2，0)作圆的两条切线，切点分别是A，B，则直线AB的方程是( )。



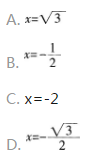    答案：B
    解析：

  • 第20题：

    已知线段AB方位角为220°，则线段BA的方位角为（）。

    • A、220°
    • B、40°
    • C、50°
    • D、130°

    正确答案:B

  • 第21题：

    已知线段AB的水平距离为200米，线段AB的方位角为133°10′22″，则线段AB的X轴方向的坐标增量为（）

    • A、+145.859
    • B、-145.859
    • C、+136.840
    • D、-136.840

    正确答案:D

  • 第22题：

    已知线段AB的两端点坐标，可计算tgαAB=△y/△x，R＝arctg△y/△x，R>0，若使αAB＝R＋180则（）。

    • A、△x＞0，△y>0
    • B、△x<0，△y>0
    • C、△x<0，△y<0
    • D、△x＞0，△y<0

    正确答案:C

  • 第23题：

    单选题
    已知线段AB方位角为220°，则线段BA的方位角为（）。
    A

    220°

    B

    40°

    C

    50°

    D

    130°


    正确答案： C
    解析： 暂无解析

相关内容