itgle.com

设平面薄板所占xOy平面上的区域D为1≤x2+y2≤4，*≥0，y≥0，其面密度为π(x，y)=x2+y2，求该薄板的质量m。

题目

设平面薄板所占xOy平面上的区域D为1≤x2+y2≤4，*≥0，y≥0，其面密度为π(x，y)=x2+y2，求该薄板的质量m。

相似考题

1.Ω是由曲面z=x2+y2，y=x，y=0，z=1在第一卦限所围成的闭区域，f（x，y，z） 在Ω上连续，则等于：

2.I=∮C|y|ds的值为下列( )项，其中C：(x2+y2)2=a2(x2-y2)，a＞0。

3. 是由曲面z=x2+y2，y=x，y=0，z=1在第一

4.若D是由x=0，y=0，x2+y2=1所围成在第一象限的区域，则二重积分等于（　　）。

更多“设平面薄板所占xOy平面上的区域D为1≤x2＋y2≤4,*≥0,y≥0,其面密度为π(x,y)=x2＋y2,求该薄板 ”相关问题

  • 第1题：

    求函数(x，y)=x2+y2在条件2x+3y=1下的极值．


    答案：
    解析：
    解设F(x，y，λ)=X2+y2+λ(2x+3y-1)，

  • 第2题：

    设P是圆x2+y2=2上的一点，该圆在点P的切线平行于直线x+y+2=0，则点P的坐标为



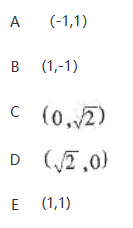    答案：E
    解析：

  • 第3题：

    设区域D为x2+y2≤4，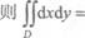

    A.4π
    B.3π
    C.2π
    D.π

    答案：A
    解析：
    A为区域D的面积．由于D为x2+y2≤4表示圆域，半径为2，因此A=π×22=4π，所以选A．

  • 第4题：

    在直角坐标系中，若平面区域D中虽有的点的坐标（x,y）均满足：0≤x≤6，0≤y≤6，|y-x|≤3，x2+y2≥9，则面积是（ ）



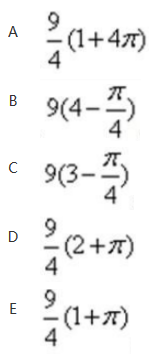    答案：C
    解析：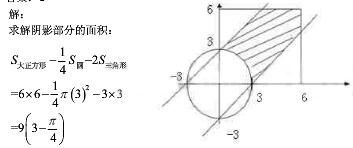

  • 第5题：

    设平面薄板所占Oxy平面上的区域D为1≤x2+y2≤4，x≥0，y≥0，其面密度
    u(x，y)=2+y2，求该薄板的质量m．


    答案：
    解析：
    由二重积分物理意义知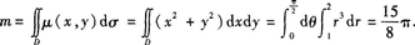
    【评析】如果被积函数为f(x2+y2)的形式，积分区域D为圆域或圆的一部分，此时将
    化为极坐标计算常常较简便．

相关内容