itgle.com

某种零件的长度服从正态分布。已知总体标准差σ=1．5，从总体中抽取200个零件组成样本，测得它们的平均长度为8．8厘米。试估计在95%置信水平下，全部零件平均长度的置信区间。

题目

某种零件的长度服从正态分布。已知总体标准差σ=1．5，从总体中抽取200个零件组成样本，测得它们的平均长度为8．8厘米。试估计在95%置信水平下，全部零件平均长度的置信区间。

相似考题

1.小样本情况下，总体服从正态分布，总体方差已知，总体均值在置信水平此题为判断题(对，错)。

2.对某大学在校15000名学生的身高进行调查，从中随机抽取了100人进行抽样调查，测得的样本平均身高为l．66m，标准差为0．08m，总体平均身高未知，现以95%的置信水平对总体平均身高进行估计。

3.下列表述中，错误的是（）。A.总体均值的置信区间都是由样本均值加减估计误差得到 B.在小样本情况下，对总体均值的估计都是建立在总体服从正态分布的假定条件下 C.当样本量n充分大时，样本均值的分布近似服从正态分布 D.当总体服从正态分布时，样本均值不服从正态分布 E.对总体均值进行区间估计时，不需要考虑总体方差是否已知

4.已知一批零件的长度X(单位：cm)服从正态分布N(μ，1)，从中随机地抽取16个零件，得到长度的平均值为40(cm)，则μ的置信度为0.95的置信区间是_______.(注：标准正态分布函数值φ(1.96)=0.975，φ(1.645)=0.95.)

更多“某种零件的长度服从正态分布。已知总体标准差σ=1．5，从总体中抽取200个零件组成样本，测得它们的平均长度为8．8厘米。试估计在95%置信水平下，全部零件平均长度的置信区间。”相关问题

  • 第1题：

    下列表述中正确的有( )。

    A.总体均值的置信区间都是由样本均值加减估计误差得到

    B.在小样本情况下，对总体均值的估计都是建立在总体服从正态分布的假定条件下

    C.当样本量n充分大时，样本均值的分布近似服从正态分布

    D.当总体服从正态分布时，无论样本量大小，样本均值一定服从正态分布

    E.对总体均值进行区间估计时，不需要考虑总体方差是否已知

    答案：A,B,D
    解析：
    选项C错误，若总体为未知的非正态总体，当样本量n充分大时，样本均值的分布近似服从正态分布；选项E错误，对总体均值进行区间估计时，需要考虑总体方差是否已知，当总体方差未知时，需要用样本方差来代替总体方差。

  • 第2题：

    已知总体服从正态分布，且总体标准差σ，从总体中抽取样本容量为n的产品，测得其样本均值为x，在置信水平为1-a=95％下，总体均值的置信区间为（　　）



    答案：A
    解析：

  • 第3题：

    已知总体服从正态分布，且总体标准差σ，从总体中抽取样本容量为n的产品，




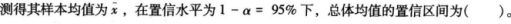
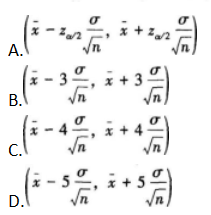    答案：A
    解析：

  • 第4题：

    已知某测验结果服从正态分布，总体方差σ2＝16，从中随机抽取 100 名被试，其平均值

    则总体平均值μ的 95%的置信区间为（）

    A.76.97＜μ＜78.03
    B.77.51＜μ＜78.49
    C.77.2＜μ＜78.78
    D.76.36＜μ＜78.64

    答案：C
    解析：

  • 第5题：

    某超市想要估平均金额，采取简单随机方式抽取49名顾客进行调查。假定从正态分布，且标准差为15元。如果样本均值为120元求总体均值95%的置信区间。

    略

  • 第6题：

    从足够大的总体中随机抽取16份统计学的考试结果作为样本。样本中的平均分为78.6，方差为64.我们想知道总体的平均分是否大于75分。假设总体的成绩服从正态分布。据材料，在95%的置信水平下，可以得出，总体的平均分数（）。

    • A、不显著大于75
    • B、显著大于75
    • C、不显著大于78.6
    • D、显著大于78.6

    正确答案:B

  • 第7题：

    为了了解所加工一批零件的长度，抽测了其中200个零件的长度，在这个问题中，200个零件的长度是（）．

    • A、总体
    • B、个体是每一个零件
    • C、总体的一个样本
    • D、样本容量

    正确答案:C

  • 第8题：

    设总体服从正态分布，方差未知，在样本容量和置信度保持不变的情形下，根据不同的样本值得到总体均值的置信区间长度将（）。

    • A、增加
    • B、不变
    • C、减少
    • D、都有可能

    正确答案:D

  • 第9题：

    已知一批零件的长度X（单位：cm）服从正态分布N（μ，1），从中随机地抽取16个零件，得到长度的平均值为40（cm），则μ的置信度为0.95的置信区间是（）.

    • A、（37.51，42.49）
    • B、（39.51，40.49）
    • C、（35.51，44.49）
    • D、（36.51，43.49）

    正确答案:B

  • 第10题：

    多选题
    下列说法错误的是（）
    A

    总体均值的置信区间都是由样本均值加减估计误差得到

    B

    在小样本情况下，对总体均值的估计都是建立在总体服从正态分布的假定条件下

    C

    当样本量n充分大时，样本均值的分布近似服从正态分布

    D

    当总体服从正态分布时，样本均值不服从正态分布

    E

    对总体均值进行区间估计时，不需要考虑总体方差是否已知


    正确答案： D,B
    解析：

  • 第11题：

    多选题
    M车间生产螺钉。为了估计螺钉的长度，从当日成品库中随机抽取25个螺钉，测量了它们的长度，样本均值为22.7mm。并且求出其长度总体均值的95%置信区间为（22.5，22.9）。下述哪些判断是不正确的（）
    A

    当日生产的螺钉中，有95%的螺钉之长度落入（22.5，22.9）之内。

    B

    当日任取一个螺钉，其长度以95%的概率落入（22.5，22.9）之内。

    C

    区间（22.5，22.9）覆盖总体均值的概率为95%。

    D

    若再次抽取25个螺钉，样本均值以95%的概率落入（22.5，22.9）之内。


    正确答案： C,D
    解析： 暂无解析

  • 第12题：

    多选题
    下列表述中，错误的是（　　）。[2011年初级真题]
    A

    总体均值的置信区间都是由样本均值加减估计误差得到

    B

    在小样本情况下，对总体均值的估计都是建立在总体服从正态分布的假定条件下

    C

    当样本量n充分大时，样本均值的分布近似服从正态分布

    D

    当总体服从正态分布时，样本均值不服从正态分布

    E

    对总体均值进行区间估计时，不需要考虑总体方差是否已知


    正确答案： B,A
    解析：
    当总体服从正态分布时，样本均值也服从正态分布。对总体均值进行区间估计时，需要分两种情况：方差已知和方差未知。

  • 第13题：

    某种零件的长度服从正态分布。已知总体标准差σ=1．5，从总体中抽取200个零件组成样本，测得它们的平均长度为8．8厘米。试估计在95%置信水平下，全部零件平均长度的置信区间。


    答案：
    解析：
    解：已知n=200，=8．8，1一a=0．95，a=0．05，当a／2=0．025时，za/2=z0.025=1．96 根据题意，该题为双侧估计，μ的置信区间为



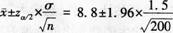
    所以，总体均值μ在0．95置信水平下的置信区间为(8．59，9．01)

  • 第14题：

    小样本情况下，总体服从正态分布，总体方差未知，总体均值在置信水平(1-a)下的置信区间为（　　）




    答案：A
    解析：

  • 第15题：

    小样本情况下，总体服从正态分布，总体方差已知，总体均值在置信水平（1-a）下的置信区间为（ ）。



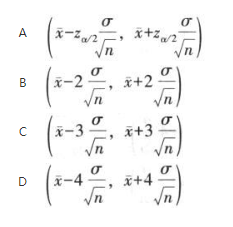    答案：A
    解析：

  • 第16题：

    从包含5000个项目的总体中抽取100个组成样本。平均值为200美元，标准差为30美元。置信水平为95%(Z=1.96)的置信区间为( )。

    A.970600～1029400美元
    B.706000～1294000美元
    C.996733～1003267美元
    D.997060～1002940美元

    答案：A
    解析：
    A精确度是1.96×30×5000/10=29400。5000×200=1000000美元±29400美元。选项B不正确，如果样本量的平方根被错误舍弃，精确度为1.96×30×5000=294000。选项C不正确，如果标准差和样本量的平方根被错误地弄颠倒了，精确度1.96×10×5000/30=3267。选项D不正确，如果错误使用了样本量，精确度为1.96×30×5000/100=2940。

  • 第17题：

    总体为正态分布、方差σ2未知。 样本量n = 20、样本的平均值为χ、标准差为 S ，当置信水平 为1-α时，总体均值μ的置信区间为（）。


    正确答案:χ±tα/2(20-1)S/√20

  • 第18题：

    下列表述中，错误的是（）。

    • A、总体均值的置信区间都是由样本均值加减估计误差得到
    • B、在小样本情况下，对总体均值的估计都是建立在总体服从正态分布的假定条件下
    • C、当样本量n充分大时，样本均值的分布近似服从正态分布
    • D、当总体服从正态分布时，样本均值不服从正态分布
    • E、A总体均值进行区间估计时，不需要考虑总体方差是否已知

    正确答案:D,E

  • 第19题：

    从一个正态分布总体中抽取样本，在总体方差已知时样本的平均数和方差分别服从（）分布和（）分布；在总体方差未知时样本的平均数服从（）分布。从两个正态分布总体中抽取样本，在总体方差已知和未知时样本平均数的差分别服从（）分布和（）分布。


    正确答案:正态；卡方；t；正态；t

  • 第20题：

    M车间生产螺钉。为了估计螺钉的长度，从当日成品库中随机抽取25个螺钉，测量了它们的长度，样本均值为22.7mm。并且求出其长度总体均值的95%置信区间为（22.5，22.9）。下述哪些判断是不正确的（）

    • A、当日生产的螺钉中，有95%的螺钉之长度落入（22.5，22.9）之内。
    • B、当日任取一个螺钉，其长度以95%的概率落入（22.5，22.9）之内。
    • C、区间（22.5，22.9）覆盖总体均值的概率为95%。
    • D、若再次抽取25个螺钉，样本均值以95%的概率落入（22.5，22.9）之内。

    正确答案:A,B,D

  • 第21题：

    从州际公路上行驶的汽车中抽取121辆作为随机样本，样本平均速度为65英里/小时。已知总体的标准差为22英里/小时。 在96.6%的置信水平下，μ的置信区间是（）。

    • A、63.00到67.00
    • B、60.76到69.24
    • C、61.08到68.92
    • D、60.00到80.00

    正确答案:B

  • 第22题：

    单选题
    已知一批零件的长度X（单位：cm）服从正态分布N（μ，1），从中随机地抽取16个零件，得到长度的平均值为40（cm），则μ的置信度为0.95的置信区间是（）.
    A

    （37.51，42.49）

    B

    （39.51，40.49）

    C

    （35.51，44.49）

    D

    （36.51，43.49）


    正确答案： C
    解析： 暂无解析

  • 第23题：

    填空题
    从一个正态分布总体中抽取样本，在总体方差已知时样本的平均数和方差分别服从（）分布和（）分布；在总体方差未知时样本的平均数服从（）分布。从两个正态分布总体中抽取样本，在总体方差已知和未知时样本平均数的差分别服从（）分布和（）分布。

    正确答案： 正态,卡方,t,正态,t
    解析： 暂无解析

  • 第24题：

    填空题
    总体为正态分布、方差σ2未知。 样本量n = 20、样本的平均值为χ、标准差为 S ，当置信水平 为1-α时，总体均值μ的置信区间为（）。

    正确答案： χ±tα/2(20-1)S/√20
    解析： 暂无解析

相关内容