itgle.com

不定积分∫xf(x)dx等于（ ）。 A. xf(x)-f(x) + C B. xf(x)-f(x) + C C. xf(x) + f(x) + C D. xf(x) +f(x)+ C

题目
不定积分∫xf(x)dx等于（ ）。
A. xf(x)-f(x) + C B. xf(x)-f(x) + C
C. xf(x) + f(x) + C D. xf(x) +f(x)+ C

相似考题

1.设f(x)在[0，1]上可导，且满足f(1)=∫01xf(x)dx，证明：必有一点ξ∈(0，1)，使得ξf(ξ)+f(ξ)=0．

2.设f(x)的一个原函数为x3，则xf(1-x2)dx=(57)。A．(1-x2)3+CB．C．D．x3+C

3.不定积分∫xf"（x）dx等于： A.xf'（x）-f'（x）+c B.xf'（x）-f（x）+c C.xf'（x）+f'（x）+c D.xf'（x）+f（x）+c

4.计算不定积分∫(x)√(2＋x^2)dx.

更多“不定积分∫xf(x)dx等于（ ）。 ”相关问题

  • 第1题：




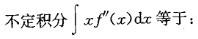
    A. xf'(x)-f'(x)+c
    B.xf'(x)-f(x)+c
    C.xf'(x)+f'(x)+c
    D.xf'(x)-f(x)+c

    答案：B
    解析：
    提示:利用分部积分公式计算再积分。



    @##

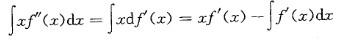
  • 第2题：

    不定积分∫xf″（x）dx等于：（）

    • A、xf′（x）-f′（x）+c
    • B、xf′（x）-f（x）+c
    • C、xf′（x）+f′（x）+c
    • D、xf′（x）+f（x）+c

    正确答案:B

  • 第3题：

    X→Y∈F+（）

    • A、X∈XF+
    • B、X∈YF+
    • C、Y∈YF+
    • D、Y∈XF+

    正确答案:D

  • 第4题：

    被积函数的乘积的不定积分等于各因子的不定积分的乘积。


    正确答案:错误

  • 第5题：

    单选题
    若f（x）的一个原函数是lnx/x，则∫xf′（x）dx＝（　　）。
    A

    lnx/x＋C

    B

    （1＋lnx）/x＋C

    C

    1/x＋C

    D

    （1－2lnx）/x＋C


    正确答案： C
    解析：
    由f（x）＝（lnx/x）′＝（1－lnx）/x2，则：
    ∫xf′（x）dx＝∫xdf（x）＝xf（x）－∫df（x）＝x（1－lnx）/x2－lnx/x＋C＝（1－2lnx）/x＋C

  • 第6题：

    判断题
    被积函数的乘积的不定积分等于各因子的不定积分的乘积。
    A

    对

    B

    错


    正确答案： 对
    解析： 暂无解析

  • 第7题：

    单选题
    设（d／dx）f（x）=g（x），h（x）=x2，则（d／dx）f［h（x）]等于：（）
    A

    g（x2）

    B

    2xg（x）

    C

    x2g（x2）

    D

    2xg（x2）


    正确答案： D
    解析： 暂无解析

  • 第8题：

    单选题
    设f（u，v）是二元可微函数，z＝f（y/x，x/y），则x∂z/∂x－y∂z/∂y＝（　　）。
    A

    －yf1′/x－xf2′/y

    B

    －yf1′/x＋xf2′/y

    C

    2（－yf1′/x＋xf2′/y）

    D

    2（－yf1′/x－xf2′/y）


    正确答案： A
    解析：
    设f1′为函数f（u，v）对第一中间变量的偏导，f2′为函数f（u，v）对第二中间变量的偏导，则∂z/∂x＝f1′·（－y/x2）＋f2′·（1/y），∂z/∂y＝f1′·（1/x）＋f2′·（－x/y2），x∂z/∂x－y∂z/∂y＝2（－yf1′/x＋xf2′/y）。

  • 第9题：

    单选题
    若z＝f（x，y）和y＝φ（x）均可微，则dz/dx等于（　　）。[2013年真题]
    A

    ∂f/∂x＋∂f/∂y

    B

    ∂f/∂x＋（∂f/∂y）（dφ/dx）

    C

    （∂f/∂y）（dφ/dx）

    D

    ∂f/∂x－（∂f/∂y）（dφ/dx）


    正确答案： A
    解析：
    dz/dx＝（∂f/∂x）（dx/dx）＋（∂f/∂y）（dφ/dx）＝∂f/∂x＋（∂f/∂y）（dφ/dx）。

  • 第10题：

    单选题
    设f（x）的一个原函数为xex，则∫xf′（x）dx＝（　　）。
    A

    xex＋C

    B

    x2ex＋C

    C

    －xex＋C

    D

    －x2ex＋C


    正确答案： C
    解析：
    采用分部积分法，∫xf′（x）dx＝∫xd[f（x）]＝xf（x）－∫f（x）dx，又由题意可知，f（x）＝（xex）′，则∫xf′（x）dx＝x（xex）′－xex＋C＝x2ex＋C。

  • 第11题：

    单选题
    若∫f（x）dx＝F（x）＋C，则∫xf（1－x2）dx＝（　　）。[2018年真题]
    A

    F（1－x2）＋C

    B

    （－1/2）F（1－x2）＋C

    C

    （1/2）F（1－x2）＋C

    D

    （－1/2）F（x）＋C


    正确答案： B
    解析：
    计算得∫xf（1－x2）dx＝（－1/2）∫f（1－x2）d（1－x2）＝（－1/2）F（1－x2）＋C，这里C均表示常数。

  • 第12题：

    单选题
    ∫xf″（x）dx＝（　　）。
    A

    xf′（x）－∫f（x）dx

    B

    xf′（x）－f′（x）＋C

    C

    xf′（x）－f（x）＋C

    D

    f（x）－xf′（x）＋C


    正确答案： B
    解析：
    ∫xf″（x）dx＝∫xd[f′（x）]＝xf′（x）－∫f′（x）dx＝xf′（x）－f（x）＋C。

  • 第13题：

    设F（x）是f（x）的一个原函数，则∫e-xf（e-x）dx等于下列哪一个函数？（）

    • A、F（e-x）+c
    • B、-F（e-x）+c
    • C、F（ex）+c
    • D、-F（ex）+c

    正确答案:B

  • 第14题：

    设（d／dx）f（x）=g（x），h（x）=x2，则（d／dx）f［h（x）]等于：（）

    • A、g（x2）
    • B、2xg（x）
    • C、x2g（x2）
    • D、2xg（x2）

    正确答案:D

  • 第15题：

    不定积分∫secx（secx－tgx）dx等于（）。

    • A、ctgx+cscx+C
    • B、cscx－ctgx+C
    • C、tgx－secx+C
    • D、secx－tgx+C

    正确答案:C

  • 第16题：

    函数z=xy2+y（lny-1）在x=1，y=1处的全微分dz等于（）．

    • A、dx+dy
    • B、dx-dy
    • C、dx+2dy
    • D、dx-2dy

    正确答案:C

  • 第17题：

    单选题
    不定积分∫secx（secx－tgx）dx等于（）。
    A

    ctgx+cscx+C

    B

    cscx－ctgx+C

    C

    tgx－secx+C

    D

    secx－tgx+C


    正确答案： C
    解析： 暂无解析

  • 第18题：

    单选题
    设f（x）的一个原函数为xex，则∫xf′（x）dx＝（　　）。
    A

    x2ex/2

    B

    x2ex＋C

    C

    2xex＋C

    D

    x2ex/2＋C


    正确答案： C
    解析：
    采用分部积分法，∫xf′（x）dx＝∫xd[f（x）]＝xf（x）－∫f（x）dx，又由题意可知，f（x）＝（xex）′，则∫xf′（x）dx＝x（xex）′－xex＋C＝x2ex＋C。

  • 第19题：

    填空题
    设f（x）的一个原函数为xex，则∫xf′（x）dx＝____。

    正确答案： x2ex+C
    解析：
    采用分部积分法，∫xf′（x）dx＝∫xd[f（x）]＝xf（x）－∫f（x）dx，又由题意可知，f（x）＝（xex）′，则∫xf′（x）dx＝x（xex）′－xex＋C＝x2ex＋C。

  • 第20题：

    单选题
    设F（x）是f（x）的一个原函数，则∫e-xf（e-x）dx等于下列哪一个函数？（）
    A

    F（e-x）+c

    B

    -F（e-x）+c

    C

    F（ex）+c

    D

    -F（ex）+c


    正确答案： B
    解析： 暂无解析

  • 第21题：

    单选题
    若sec2x是f（x）的一个原函数，则∫xf（x）dx等于（　　）。[2016年真题]
    A

    tanx＋C

    B

    xtanx－ln｜cosx｜＋C

    C

    xsec2x＋tanx＋C

    D

    xsec2x－tanx＋C


    正确答案： C
    解析：
    由于sec2x是f（x）的一个原函数，令F（x）＝sec2x＋C，则：∫xf（x）dx＝∫xd[F（x）]＝xF（x）－∫F（x）dx＝xsec2x＋Cx－（tanx＋Cx－C）＝xsec2x－tanx＋C。

  • 第22题：

    单选题
    不定积分∫xf″（x）dx等于：（）
    A

    xf′（x）-f′（x）+c

    B

    xf′（x）-f（x）+c

    C

    xf′（x）+f′（x）+c

    D

    xf′（x）+f（x）+c


    正确答案： D
    解析： 利用分部积分公式计算。∫xf″=fxdf′（x）=xf′（x）-∫f′（x）dx=xf′（x）-f（x）+c

  • 第23题：

    单选题
    设f（u，v）是二元可微函数，z＝f（y/x，x/y），则x∂z/∂x－y∂z/∂y＝（　　）。
    A

    2（yf1′/x＋xf2′/y）

    B

    2（yf1′/x－xf2′/y）

    C

    2（－yf1′/x＋xf2′/y）

    D

    2（－yf1′/x－xf2′/y）


    正确答案： C
    解析：
    设f1′为函数f（u，v）对第一中间变量的偏导，f2′为函数f（u，v）对第二中间变量的偏导，则∂z/∂x＝f1′·（－y/x2）＋f2′·（1/y），∂z/∂y＝f1′·（1/x）＋f2′·（－x/y2），x∂z/∂x－y∂z/∂y＝2（－yf1′/x＋xf2′/y）。

相关内容