某公司组织业务知识竞赛,有三支队伍进入决赛。决赛为40道抢答题,答对加10分,答错扣10分,抢到不答扣5分。结束后计算总分,发现三支队伍得分均不少于20分,每队都有至少1题抢到未答。红队和黄队分数相同,比蓝队多30分。已知红队答对x道,黄队答对的和蓝队答错的都是(x-2)道。问红队至少抢到了多少题?A.11 B.12 C.13 D.14
题目
B.12
C.13
D.14
相似考题
参考答案和解析
黄队比红队少答对2道题,但红、黄两队总分一致,说明红队比黄队:①多错了2道;②多不答4道;③多答错1道同时多不答2道。要求红答题总量最少,则红队先假设只错2道题,如下表:

由于每队得分均不少于20分,红队和黄队比蓝队多30分,因此蓝队至少20分,红队=黄队,且至少50分?由于每队至少有一道抢到未答,为了让红队答题数最少,假设红队黄队得分均为55分,如下表:
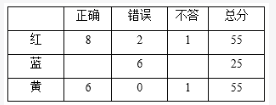
红队答对的为8道,至少抢到了11道题。
更多“ 某公司组织业务知识竞赛,有三支队伍进入决赛。决赛为40道抢答题,答对加10分,答错扣10分,抢到不答扣5分。结束后计算总分,发现三支队伍得分均不少于20分,每队都有至少1题抢到未答。红队和黄队分数相同,比蓝队多30分。已知红队答对x道,黄队答对的和蓝队答错的都是(x-2)道。问红队至少抢到了多少题?”相关问题
-
第1题:
需要详细的解答!!!!!!!!!!!某校八年级学生数学竞赛共有20道题目,每答对一道得5分,不答或答错扣1分,欲得80分以上至少要答对的题目数是多少? A. 15道 B. 16道 C. 17道 D. 18道
解答如下:
设打对x道,不答y,打错z。
有题意可等如下关系:
x+y+z = 20 ----1
5x-(y+z)>=80 ---2
将等式1带入不等式2可得不等式
5x-(20-x)>=80 ---3
化简得 6x>=100
解得x>=50/3
又因为x是整数,所以可得x的最少取值为 17.选择C
列方程:
首先设 答对为 x道,那答错为: 20-x 道
5x-(20-x)>80
解得 x>50/3 因为x为整数,50/3是16.666666.。。
所以x应该是17,所以选C
选C。 这道题中问题中有“至少”,所以可以直接从选项A开始代入验证,显然能够直接排除AB,因为答对得到的分都没多于80分。
您好!
欲得80分以上至少要答对80/5=16道,16道答对,4道不答或答错分数为80-4=76不符合,17道答对,3道不答或答错分数为85-3=82刚好符合,所以欲得80分以上至少要答对的题目数是17
这道题中问题中有“至少”,所以可以直接从选项A开始代入验证,显然能够直接排除AB,因为答对得到的分都没多于80分。验证C发现正确。我是老师也作公务员考试培训工作,以后可以联系我我给你培训。这道题中问题中有“至少”,所以可以直接从选项A开始代入验证,显然能够直接排除AB,因为答对得到的分都没多于80分。验证C正确。设答对X道,则5*X+20-X》=80,4X》=60,X》=15
-
第2题:
某次考试,有两种打分方式。一种是答对一题得5分,不答得2分,答错不得分:另一种方法是先给40分,然后答对得3分,不答不得分,答错扣2分。用这两种方式计算,某考生最后都拿到81分。请问,这次考试有多少道题?
 正确答案:C
正确答案:C
解析:第二种算法跟第一种算法相比,无论做对、做错或不答,正好每一道题少得2分,因此总题数应该是40+2=20道。 -
第3题:
某次知识竞赛共出了 25道题,评分标准如下:答对1题加4分;答错1题扣1分;不答记0 分。已知小明不答的题比答错的题多,他的总分为67分,则他有几道题没有回答?( )
A. 4
B. 6
C. 7
D. 8答案:C解析:设小明答对题数为X道,答错的题数为y道,不答的题数为z道,则可得: 因为不答的题比答错的多,因此y<z,代入可得
因为不答的题比答错的多,因此y<z,代入可得 ,解的0≤y≤3,而只有当Y=1时,x的取值才是整数,为x=17,此时z=17.故本题正确答案为C。
,解的0≤y≤3,而只有当Y=1时,x的取值才是整数,为x=17,此时z=17.故本题正确答案为C。 -
第4题:
一次数学考试共有50道题,规定答对一题得2分,答错一题扣1分,未答的题不计分。考试结束后,小明共得73分。求小明这次考试中答对的题目比答错和未答的题目之和可能相差多少个?()
- A、25
- B、29
- C、32
- D、35
正确答案:C -
第5题:
有一份选择题试卷共6道小题,其得分标准是:一道小题答对得8分,答错得0分,不答得2分。某位同学得了20分,则他( )。
- A、至少答对一道小题
- B、至少有三道小题没答
- C、至少答对三道小题
- D、答错两道小题
正确答案:D -
第6题:
单选题一次数学竞赛出10道选择题,评分标准为:基础分10分,答对一题得3分,答错一题扣1分,不答不得分。要保证有4人得分相同,至少要有多少人参加比赛?( )A80
B100
C115
D120
正确答案: A解析:
一共做10题:最高分40,最低0分;做对9题:最高37分,最低36分;做对8题:最高34分,最低32分;做对7题:最高31分,最低28分;……做对0题:最高10分;最低0分。可知只有39分、38分、35分得不到,故可以得到的分数种类有:41-3=38种,所以要想4人得分一样,最少的参赛人数是3×38+1=115人。 -
第7题:
某校八年级学生数学竞赛共有20道题目,每答对一道得5分,不答或答错扣一分,80分以上至少要答对的题目数是多少?( )
A.15道
B.16道
C.17道
D.18道
正确答案:C由题目可知,如果不考虑扣分,要拿到80分,则必须答对16道题,而因为不答或答错扣一分,所以四题扣四分为76分,为保证80分以上,至少要答对17道题,所以答案为C项。
-
第8题:
如果蓝队没有获得冠军,那么红队将获得冠军;如果蓝队获得冠军,那么绿队将获得季军;如果红队获得亚军,那么黄队将获得冠军;除非黄队获得冠军,否则绿队不会获得季军。
假如前述预测都是正确的,那么可以推出()。A.蓝队获得冠军
B.红队获得冠军
C.绿队获得冠军
D.黄队获得冠军答案:B解析:考査复言命题推理。题干条件可表示为:①蓝队没有获得冠军→红队获得冠军;②蓝队获得冠军→绿队获得季军;③红队获得亚军→黄队获得冠军;④黄队获得冠军←绿队获得季军。
②和④组成连锁推理:蓝队获得冠军→绿队获得季军→黄队获得冠军,该推理前后矛盾,可知蓝队不可能获得冠军,再根据①可知红队获得冠军。故答案选B。 -
第9题:
某公司组织业务知识竞赛,有三支队伍进入决赛。决赛为40道抢答题,答对加10分,答错扣10分,抢到不答扣5分。结束后计算总分,发现三支队伍得分均不少于20分,每队都有至少1题抢到未答。红队和黄队分数相同,比蓝队多30分。已知红队答对x道,黄队答对的和蓝队答错的都是(x-2)道。问红队至少抢到了多少题?A.11
B.12
C.13
D.14答案:A解析:黄队比红队少正确2道题,但红黄总分一致,说明红队比黄队多错了2道或多不答4道或多答错1道同时多不答2道,要求红答题总量最少,则红队先假设只错2道题,如下表:

由于每队得分均不少于20分,红队和黄队比蓝队多30分,因此蓝队至少20分,红队=蓝队至少50分。由于每队至少有一道抢到未答,为了让红队答题数最少,假设红队黄队得分均为55分,如下表:
红队答对的为8道。

-
第10题:
有一份选择题试卷共6个小题,其得分标准是:一道小题答对得8分,答错得0分,不答得2分,某位同学得了20分,则他()
- A、至多答对一道题
- B、至少有三个小题没答
- C、至少答对三个小题
- D、答错两个小题
正确答案:D -
第11题:
单选题龙舟竞赛前,人们对参赛的红、黄、蓝、绿四个队的成绩作了三种估计:①蓝队获冠军,黄队获亚军;②蓝队获亚军,绿队得第三名;③红队获亚军,绿队得第四名。然而,实际的比赛结果显示以上三种估计中,每种均对了一半,错了一半。由此推出,比赛结果一到四名的顺序为( )。A蓝队、绿队、黄队、红队
B绿队、黄队、红队、蓝队
C蓝队、红队、绿队、黄队
D红队、黄队、蓝队、绿队
正确答案: D解析:
方法一:由三种估计可知,①②的前半句均涉及蓝队,二者不能同时为真,而每种估计都对一半错一半,如果蓝队获亚军,则①全为假,出现矛盾,因此蓝队只能获冠军,绿队得第三名。由于②的后半句为真,因此③的后半句假,即红队获得亚军。那么黄队只能是第四名。因此答案选C。
方法二:假设①中黄队是亚军为真,根据②可知绿队第三名,根据③可知绿队为第四名,出现矛盾;假设①中蓝队是冠军正确,那么根据②可知绿队是第三名,根据③可知红队是亚军,则黄队是第四名,与题意相符。因此答案选C。
