itgle.com

两封信随机地投向标号1,2,3,4的四个空邮筒,问:(1)第二个邮筒中恰好投入一封信的概率是多少;(2)两封信都投入第二个邮筒的概率是多少?

题目
两封信随机地投向标号1,2,3,4的四个空邮筒,问:(1)第二个邮筒中恰好投入一封信的概率是多少;(2)两封信都投入第二个邮筒的概率是多少?

相似考题

1.将3封信随机投入到编号为1、2、3、4的四个邮筒内,用X表示有信邮筒的最小号码,Y表示第1号邮筒中信的个数,求(X,Y)的联合分布列。

2.三封信投入五个邮筒，共有（）种不同投法A.5^3 B.35 C.5 D.15

3.两封信随机地投入标号为1，2，3，4的4个邮筒，则1，2号邮筒各有一封信的概率等于

4.把两封信随机地投入标号为1，2，3，4的4个邮筒中，则1，2号邮筒各有一封信的概率等于

参考答案和解析
参考答案： 
更多“两封信随机地投向标号1,2,3,4的四个空邮筒,问:(1)第二个邮筒中恰好投入一封信的概率是多少;(2)两封信都投入第二个邮筒的概率是多少? ”相关问题

  • 第1题：

    把两封信随机地投入标号为1，2，3，4的4个邮筒中，则1，2号邮筒各有一封信的概率等于()


    答案：C
    解析：
    【考情点拨】本题考查了古典概率的知识点．【应试指导】因两封信投向四个邮筒共有的投法(可重复排列)为n=42=16；满足1，2号邮筒各有一封信的投法为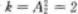

    ，故所求概率为

  • 第2题：

    将两封信随机地投入四个邮筒中，则未向前两个邮筒投信的概率为（）。

    A．答案


    设事件A，B，C分别表示“第1个邮筒恰好投入一封信”，“前两个邮筒各投入一封信”，”前面邮箱内没有信” 样本空间Ω中包含基本事件总数n=4 2 =16． 事件A中包含基本事件个数 ，则 $事件B中包含基本事件个数m 2 =2!=2，则 $事件C中包含基本事件个数m 3 =2 2 =4，则

  • 第3题：

    两封信随机地投向标号为1,2,3,4的四个邮筒，问第2个邮筒恰好投入一封信的概率3/8为, 是否正确？


    (Ⅰ)根据题意，(X，Y)的全部可能取值为(0，1)，(0，2)，(0，3)，(1，2)，(1，3)，(2，2)，(3，1)，再分别计算相应的概率． 事件{x=0，Y=1}表示“三封信均投入后3个邮筒中的某一个邮筒内”．根据古典概型公式，样本空间所含样本点数为4\r\n 3 \r\n=64，有利于事件{X=0，y=1}的样本点数为C\r\n 3 \r\n和υ\r\n 1 \r\n=3，于是\r\n \r\n类似地可以计算出各有关概率值，列表如下：\r\n \r\n(Ⅱ)从表中看出，只取1，2，3三个可能值，相应概率分别是对表中p\r\n ij \r\n的各列求和，所以Y的边缘分布为表中最下行值．\r\n \r\n在X=0条件下，关于Y的条件分布，可以应用上述公式计算出来，列表如下：\r\n

  • 第4题：

    将两封信随机地投入四个邮筒中，则未向前面两个邮筒投信的概率为（).

    A．1/4

    B．1/6

    C．1/3

    D．1/12


    1/4

  • 第5题：

    两封信随机地投入四个邮箱，求前两个邮箱内没有信的概率以及第一个邮箱内只有一封信的概率。


    设事件A，B，C分别表示“第1个邮筒恰好投入一封信”，“前两个邮筒各投入一封信”，”前面邮箱内没有信” 样本空间Ω中包含基本事件总数n=4 2 =16． 事件A中包含基本事件个数 ，则 $事件B中包含基本事件个数m 2 =2!=2，则 $事件C中包含基本事件个数m 3 =2 2 =4，则

相关内容