itgle.com

不同的五种商品在货架上排成一排，其中甲、乙两种必须排在一起，丙、丁两种不能排在一起，则不同的排法种数共有（ ）。A．12种B．20种C．24种D．48种

题目

不同的五种商品在货架上排成一排，其中甲、乙两种必须排在一起，丙、丁两种不能排在一起，则不同的排法种数共有（ ）。

A．12种

B．20种

C．24种

D．48种

相似考题

1.3名学生和2名老师站成一排照相，2名老师必须站在一起且不在边上的不同排法共有：A、12种 B、24种 C、36种 D、48种

2.甲、乙、丙、丁四个同学排成一排，从左往右数，如果甲不排在第一个位置上，乙不排在第二个位置上，丙不排在第三个位置上，丁不排在第四个位置上，那么不同的排法共有（ ）种。A．8B．9C．10D．12

3.（9）某单位安排7位员工在10月1日至7日值班，每天1人，每人值班1天，若7位员工中的甲、乙排在相邻两天，丙不排在10月1日，丁不排在10月7日，则不同的安排方案共有A．504种B．960种C．1008种D．1108种

4.4男2女6个人站成一排合影留念，要求2个女的紧挨着排在正中间，有（ ）种不同的排法。 A．26 B．36 C．60 D．48

更多“不同的五种商品在货架上排成一排，其中甲、乙两种必须排在一起，丙、丁两种不能排在一起，则不同的排法种数共有（ ）。A．12种B．20种C．24种D．48种”相关问题

  • 第1题：

    甲、乙、丙、丁四个同学排成一排，从左到右数，如果甲不排在第一个位置上，乙不排在第二个位置上，丙不排在第三个位置上，丁不排在第四个位置上，那么不同的排法共有多少种？（ ）

    A. 9

    B. 11

    C. 14

    D. 6


    正确答案：A
    A［解析］我们可以这样考虑，第一个位置，乙、丙、丁都可以排，若乙排在第一个位置上，乙不能排的位置甲、丙、丁三人都能排，最后剩下的两人只有一种排法，所以不同的排法有3×3＝9（种）。

  • 第2题：

    四对情侣排成一队买演唱会门票，已知每对情侣必须排在一起，问共有多少种不同的排队顺序？

    A.24种
    B.96种
    C.384种
    D.40320种

    答案：C
    解析：
    每对情侣必须排在一起，则每对情侣看成一个整体，四对情侣的排队方式有A44=24种，每对情侣又有2种排列方式，因此共有24x24=384种排队方式。

  • 第3题：

    现有4个成年人和2个小孩,其中2人是母女;6人排成一排照相,要求每个小孩两边都是成年人,且1对母女要排在一起,则不同的排法有（ ）种

    A.56
    B.60
    C.72
    D.84
    E.96

    答案：C
    解析：

  • 第4题：

    有5个人排队,甲、乙必须相邻,丙不能在两头,则不同的排法共有（ ）.

    A.12种
    B.24种
    C.36种
    D.48种
    E.60种

    答案：B
    解析：

  • 第5题：

    某单位安排7位员工在10月1日至7日值班，每天1人，每人值班1天，若7位员工中的甲、乙排在相邻两天，丙不排在10月1日，丁不排在10月7日，则不同的安排方案共有（　　）

    A、504种
    B、960种
    C、1008种
    D、1108种

    答案：C
    解析：

  • 第6题：

    甲乙丙丁四个同学排成一排，从左往右数，如果甲不排在第一个位置上，乙不排在第二个位置上，丙不排在第三个位置上，丁不排在第四个位置上，那么不同的排法共有（）种。

    • A、8
    • B、11
    • C、10
    • D、9

    正确答案:D

  • 第7题：

    大学生剧团从8名学生中选出4人分别担任甲、乙、丙、丁四个不同的表演角色，若其中有两名学生不能担任甲角色，则不同的挑选方案共有（）。

    • A、1200种
    • B、1240种
    • C、1260种
    • D、2100种

    正确答案:C

  • 第8题：

    两种商品在功能上相似，往往相互替代，比如麦当劳和肯德基，这两种商品叫做（）；如果两种商品必须一起消费，如汽车和汽油，则这两种商品叫做（）。 


    正确答案:替代品；互补品

  • 第9题：

    甲、乙、丙三个同学排成一排，有（）种排法。

    • A、6
    • B、7
    • C、8

    正确答案:A

  • 第10题：

    单选题
    甲、乙、丙三个同学排成一排，有（）种排法。
    A

    6

    B

    7

    C

    8


    正确答案： B
    解析： 暂无解析

  • 第11题：

    填空题
    两种商品在功能上相似，往往相互替代，比如麦当劳和肯德基，这两种商品叫做（）；如果两种商品必须一起消费，如汽车和汽油，则这两种商品叫做（）。

    正确答案： 替代品,互补品
    解析： 暂无解析

  • 第12题：

    3名学生和2名老师站成一排照相，2名老师必须站在一起且不在边上的不同排法共有：

    A. 12种
    B. 24种
    C. 36种
    D. 48种

    答案：B
    解析：
    2名老师可以站在2，3位或者3，4位。每一种的不同排法是3！×2=12。则总共有12×2=24种排法。故答案为B。

  • 第13题：

    有7本互不相同的书,其中数学书2本、语文书2本、美术书3本,若将这些书排成一列放在书架上,则数学书恰好排在一起,同时语文书也恰好排在一起的排法共有（ ）种

    A.240
    B.480
    C.960
    D.1280
    E.1440

    答案：B
    解析：

  • 第14题：

    有5本不同的书排成一排,其中甲、乙必须排在一起,丙、丁不能排在一起,则不同的排法共（ ）种

    A.12种
    B.24种
    C.36种
    D.48种
    E.60种

    答案：B
    解析：

  • 第15题：

    5 个人从船头到船尾排成一列一起划船，其中甲不能排在船头，乙不能排在船尾，则有（ ）种排列方法。

    A.78
    B.48
    C.52
    D.36

    答案：A
    解析：
    5个人排成一列共有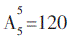种，其中甲排在船头有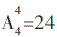种，乙排在船尾的排法有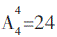种，甲排在船头且乙排在船尾的排法有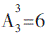种，根据两个集合的容斥原理，所求共有 120－24－24＋6＝78 种。

  • 第16题：

    不同的五种商品在货架上排成一排，其中甲、乙两种必须排在一起，丙、丁两种不能排在一起，则不同的排法种数共有(　　)．

    A.12种
    B.20种
    C.24种
    D.48种

    答案：C
    解析：

    (种)．选C．

  • 第17题：

    某台小型晚会由6个节目组成，演出顺序有如下要求：节目甲必须排在前两位、节目乙不能排在第一位，节目丙必须排在最后一位，该台晚会节目演出顺序的编排方案共有（）。

    • A、36种
    • B、42种
    • C、48种
    • D、54种

    正确答案:B

  • 第18题：

    电影院售票处只有4对情侣排成一队买电影票，已知其中3对情侣，每一对情侣均排在一起，另外一对情侣因为闹别扭不想站在一起，问共有多少种不同的排队顺序？（）

    • A、24种
    • B、96种
    • C、384种
    • D、576种

    正确答案:D

  • 第19题：

    甲、乙、丙、丁三人站成一排，甲必须站在排头，一共有（）种排法。

    • A、6
    • B、8
    • C、4

    正确答案:A

  • 第20题：

    四对情侣排成一队买演唱会门票，已知每对情侣必须排在一起，问共有多少种不同的排队顺序（）

    • A、24种
    • B、96种
    • C、384种
    • D、40320种

    正确答案:C

  • 第21题：

    单选题
    甲、乙、丙、丁三人站成一排，甲必须站在排头，一共有()种排法。
    A

    6

    B

    8

    C

    4


    正确答案： C
    解析： 暂无解析

  • 第22题：

    单选题
    某台小型晚会由6个节目组成，演出顺序有如下要求：节目甲必须排在前两位、节目乙不能排在第一位，节目丙必须排在最后一位，该台晚会节目演出顺序的编排方案共有（）。
    A

    36种

    B

    42种

    C

    48种

    D

    54种


    正确答案： C
    解析： 暂无解析

相关内容