itgle.com

数学史上一共发生了几次危机 ( ) A、1 B、2 C、3 D、4

题目
数学史上一共发生了几次危机 ( )

A、1
B、2
C、3
D、4
相似考题

1.中国近代史上有几次禁烟运动？

2.数学史上共发生过三次数学危机。()此题为判断题(对，错)。

3.春秋战国时陈国一共被灭了几次？

4.将数学悖论和三次数学危机联系在一起来谈，确实是一个不错的想法。三次数学危机都是数学史上的精彩情节,_______;而那些蕴含哲理的数学悖论更是_______。每个悖论的破译，都可从正反两个方面加深对数学基本概念和基本方法的理解。填入划横线部分最恰当的一项是（ ）。A．耐人寻味 引人入胜B．引人人胜 发人深省C．字字珠玑 振聋发聩D．振聋发聩 耐人寻味

参考答案和解析
答案：C
解析：
一共发生了三次，分别是：无理数的发现，无穷小是零吗，罗素悖论的产生。
更多“数学史上一共发生了几次危机 ( ) ”相关问题

  • 第1题：

    数学史上一共发生了几次危机( )


    A.1

    B.2

    C.3

    D.4

    答案：C
    解析：
    一共发生了三次，分别是：无理数的发现，无穷小是零吗，罗素悖论的产生。

  • 第2题：

    数学发展史上曾经历过三次危机,触发第三次数学危机的事件是( )。

    A.无理数的发现
    B.微积分的创立
    C.罗素悖论
    D.数学命题的机器证明

    答案：C
    解析：
    第三次数学危机为数学罗素悖论的产生。第三次数学危机引发了关于数学逻辑基础可靠性的问题,导致无矛盾的集合论公理系统的产生。在这场危机中集合论得到较快的发展,数学基础的进步更快,数理逻辑也更加成熟。到现在,从整体来看,第三次数学危机还没有解决到令人满意的程度。

  • 第3题：

    第一次数学危机，是数学史上的一次重要事件，发生于大约公元前400年左右的古希腊时期，自（）的发现起，到公元前370年左右，以（）的定义出现为结束标志。这次危机的出现冲击了一直以来在西方数学界占据主导地位的毕达哥拉斯学派。
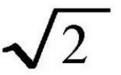    ；无理数
    略

  • 第4题：

    行拥抱礼时，一共拥抱几次？


    正确答案: 三次

  • 第5题：

    水笙一共男扮女装几次

    • A、1次 
    • B、2次 
    • C、3次 
    • D、4次

    正确答案:B

  • 第6题：

    随着数学的迅速发展，产生了新的几何学（），这是几何学的变革，标志着欧式几何一统天下的局面的结束，是数学史上重大成就之一。


    正确答案:非欧几何

  • 第7题：

    在数学研究史上，比较一致地认为从古至今，数学发展经历了（）次大危机。

    • A、三
    • B、四
    • C、五
    • D、六

    正确答案:A

  • 第8题：

    论述数学史上的三次数学危机。


    正确答案: 第一次数学危机─—无理数的发现（第一次数学危机表明，几何学的某些真理与算术无关，几何量不能完全由整数及其比来表示。反之，数却可以由几何量表示出来。整数的尊祟地位受到挑战，古希腊的数学观点受到极大的冲击。于是，几何学开始在希腊数学中占有非凡地位。同时也反映出，直觉和经验不一定靠得住，而推理证实才是可靠的。从此希腊人开始从“自明的”公理出发，经过演绎推理，并由此建立几何学体系。）
    第二次数学危机——无穷小是零吗（直到19世纪，柯西具体而有系统地发展了极限理论。柯西认为把无穷小量作为确定的量，即使是零，都说不过去，它会与极限的定义发生矛盾。无穷小量应该是要怎样小就怎样小的量，因此本质上它是变量，而且是以零为极限的量，至此柯西澄清了前人的无穷小的概念，另外Weistrass创立了极限理论，加上实数理论，集合论的建立，从而把无穷小量从形而上学的束缚中解放出来，第二次数学危机基本解决，第二次数学危机的解决使微积分更完善。）
    第三次数学危机——罗素悖论的产生（引发了关于数学逻辑基础可靠性的问题，导致无矛盾的集合论公理系统（即所谓ZF公理系统）的产生。在这场危机中集合论得到较快的发展，数学基础的进步更快，数理逻辑也更加成熟。）

  • 第9题：

    单选题
    数学的第一次危机，推动了数学的发展。导致产生了（）
    A

    欧几里得几何

    B

    非欧几里得几何

    C

    微积分

    D

    集合论


    正确答案： A
    解析： 暂无解析

  • 第10题：

    单选题
    在数学研究史上，比较一致地认为从古至今，数学发展经历了（）次大危机。
    A

    三

    B

    四

    C

    五

    D

    六


    正确答案： A
    解析： 暂无解析

  • 第11题：

    单选题
    第几次数学危机导致出现无理数（）？
    A

    4.0

    B

    3.0

    C

    2.0

    D

    1.0


    正确答案： D
    解析： 暂无解析

  • 第12题：

    问答题
    春秋战国时陈国一共被灭了几次？

    正确答案： 3次。
    解析： 暂无解析

  • 第13题：

    数学发展史上曾经发生过三次危机，触发第三次危机的事件是（　　）。


    A.无理数的发现
    B.微积分的创立
    C.罗素悖论
    D.数学命题的机器证明

    答案：C
    解析：
    本题主要考查对数学历史的了解。

    第三次数学危机为罗素悖论的产生，其引发了关于数学逻辑基础可靠性的问题，导致无矛盾的集合论公理系统的产生。

  • 第14题：

    （）年在英国发生了资本主义历史上第一次周期性的经济危机。此后，每隔十年左右，危机就会周期性地不断重复出现。

    A1825

    B1835

    C1845

    D1855


    A
    略

  • 第15题：

    第几次数学危机导致出现无理数（）？

    • A、4.0
    • B、3.0
    • C、2.0
    • D、1.0

    正确答案:D

  • 第16题：

    成都历史上几次成为地方政权？


    正确答案: 1.成都先后在7个朝代建立了8个地方政权
    2.公孙述在西汉末年建立的“大成政权”
    3.刘备在东汉末建立的“蜀汉政权”
    4.李雄在西晋末年建立的“成汉政权”
    5.王建在五代建立的“前蜀政权”
    6.孟知祥在五代建立的“后蜀政权”
    7.王小波、李顺在北宋建立的农民政权
    8.张献忠在明末建立的“大西政权”

  • 第17题：

    论述数学的三次危机对数学发展的作用。


    正确答案: 第一次数学危机促使人们去认识和理解无理数，导致了公理几何与逻辑的产生。
    第二次数学危机促使人们去深入探讨实数理论，导致了分析基础理论的完善和集合论的产生。
    第三次数学危机促使人们研究和分析数学悖论，导致了数理逻辑和一批现代数学的产生。
    由此可见，数学危机的解决，往往给数学带来新的内容，新的进展，甚至引起革命性的变革，这也反映出矛盾斗争是事物发展的历史动力这一基本原理。整个数学的发展史就是矛盾斗争的历史，斗争的结果就是数学领域的发展。

  • 第18题：

    历史上有（）数学危机。

    • A、一次
    • B、两次
    • C、三次
    • D、四次

    正确答案:C

  • 第19题：

    数学的第一次危机，推动了数学的发展。导致产生了（）

    • A、欧几里得几何
    • B、非欧几里得几何
    • C、微积分
    • D、集合论

    正确答案:A

  • 第20题：

    问答题
    论述数学史上的三次数学危机。

    正确答案： 第一次数学危机─—无理数的发现（第一次数学危机表明，几何学的某些真理与算术无关，几何量不能完全由整数及其比来表示。反之，数却可以由几何量表示出来。整数的尊祟地位受到挑战，古希腊的数学观点受到极大的冲击。于是，几何学开始在希腊数学中占有非凡地位。同时也反映出，直觉和经验不一定靠得住，而推理证实才是可靠的。从此希腊人开始从“自明的”公理出发，经过演绎推理，并由此建立几何学体系。）
    第二次数学危机——无穷小是零吗（直到19世纪，柯西具体而有系统地发展了极限理论。柯西认为把无穷小量作为确定的量，即使是零，都说不过去，它会与极限的定义发生矛盾。无穷小量应该是要怎样小就怎样小的量，因此本质上它是变量，而且是以零为极限的量，至此柯西澄清了前人的无穷小的概念，另外Weistrass创立了极限理论，加上实数理论，集合论的建立，从而把无穷小量从形而上学的束缚中解放出来，第二次数学危机基本解决，第二次数学危机的解决使微积分更完善。）
    第三次数学危机——罗素悖论的产生（引发了关于数学逻辑基础可靠性的问题，导致无矛盾的集合论公理系统（即所谓ZF公理系统）的产生。在这场危机中集合论得到较快的发展，数学基础的进步更快，数理逻辑也更加成熟。）
    解析： 暂无解析

  • 第21题：

    单选题
    历史上有（）数学危机。
    A

    一次

    B

    两次

    C

    三次

    D

    四次


    正确答案： C
    解析： 暂无解析

  • 第22题：

    填空题
    随着数学的迅速发展，产生了新的几何学（），这是几何学的变革，标志着欧式几何一统天下的局面的结束，是数学史上重大成就之一。

    正确答案： 非欧几何
    解析： 暂无解析

  • 第23题：

    问答题
    行拥抱礼时，一共拥抱几次？

    正确答案： 三次
    解析： 暂无解析

相关内容