已知曲面方程为x-yZ+z2-2x+8y+6z=10,则过点(5,-2.1)的切平面方程为( )。 A、2x+3y+2z=0 B、2x+y+2z=lO C、x-2y+6z=15 D、x-2y+6z=0
题目
已知曲面方程为x-yZ+z2-2x+8y+6z=10,则过点(5,-2.1)的切平面方程为( )。
A、2x+3y+2z=0
B、2x+y+2z=lO
C、x-2y+6z=15
D、x-2y+6z=0
B、2x+y+2z=lO
C、x-2y+6z=15
D、x-2y+6z=0
相似考题
参考答案和解析
答案:B
解析:





更多“已知曲面方程为x-yZ+z2-2x+8y+6z=10,则过点(5,-2.1)的切平面方程为( )。 ”相关问题
-
第1题:
已知点P在Oxy平面内的运动方程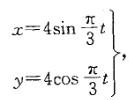 则点的运动为:
则点的运动为:
A.直线运动 B.圆周运动 C.椭圆运动 D.不能确定答案:B解析:提示:将两个运动方程平方相加。 -
第2题:
已知圆过A(1,3),B(5,1)两点,且圆心在y轴上,则圆的标准方程为__________。答案:解析:
-
第3题:
求曲面 的平行于平面
的平行于平面 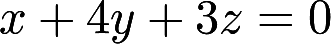 的切平面方程答案:解析:
的切平面方程答案:解析:
-
第4题:
已知曲线的方程为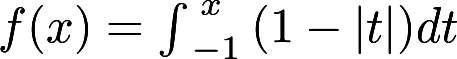 ,则曲线
,则曲线 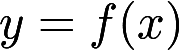 与x 轴围成的平面图形的面积为答案:解析:
与x 轴围成的平面图形的面积为答案:解析: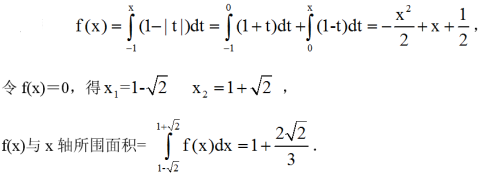
-
第5题:
曲面z=x(1-siny)+y^2(1-sinx)在点(1,0,1)处的切平面方程为________.答案:1、2x-y-z=1.解析:
-
第6题:
已知曲面方程为χ2+y2+z2-2χ+8y+6z=10,则过点(5,-2,1)的切平面方程为( )。A、2χ+y+2z=0
B、2χ+y+2z=10
C、χ-2y+6z=15
D、χ-2y+6z=0答案:B解析: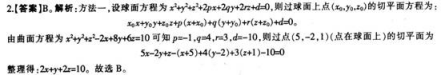

-
第7题:
过点Mo(1,-1,0)且与平面x-y+3z=1平行的平面方程为_______.答案:解析:由于已知平面的法线向量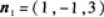 所求平面与已知平面平行,可取所求平面法线向量
所求平面与已知平面平行,可取所求平面法线向量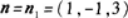 又平面过点Mo(1,-1,0),由平面的点法式方程可知,所求平面为
又平面过点Mo(1,-1,0),由平面的点法式方程可知,所求平面为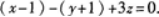
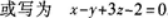 【评析】上述两种形式都正确.前者为平面的点法式方程;后者为平面的一般式方程.
【评析】上述两种形式都正确.前者为平面的点法式方程;后者为平面的一般式方程. -
第8题:
已知圆O的方程为x2+y2=1,过点P(-2,0)作圆的两条切线,切点分别是A,B,则直线AB的方程是( )。
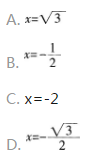 答案:B解析:
答案:B解析:
-
第9题:
已知点的运动方程为①x=5cos5t2,y=5sin5t2;②x=t2,y=2t,由此可得其轨迹方程为①(),②()。
正确答案:x2+y2=25;y2=4x -
第10题:
已知平面简谐波的波动方程式为y=8cos2π(2t-x/100)(cm),则t=2.1s时,在X=0处相位为(),在x=0.1m处相位为()。
正确答案:8.4π;8.40π -
第11题:
多选题APT自动编程语句中,如下()等方法可以定义圆。A圆心和半径
B已知不共线三点
C过已知点平行于已知平面
D平面方程
E圆心和切线
正确答案: A,D解析: 暂无解析 -
第12题:
填空题曲面z-ez+2xy=3在点(1,2,0)处的切平面方程为____。正确答案: 4(x-1)+2(y-2)=0解析:
构造函数F(x,y,z)=z-ez+2xy-3,则Fx′=2y,Fy′=2x,Fz′=1-ez。故将点(1,2,0)代入上式,即可得此点处切平面的法线向量为n=(4,2,0),则切平面方程为4(x-1)+2(y-2)=0。 -
第13题:
已知平面π过点(1,1,0)、(0,0,1)、(0,1,1),则与平面π垂直且过点(1,1,1)的直线的对称方程为 ( )。
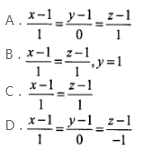 答案:B解析:平面π的法向量所求直线的方向向量为i+k,故应选B。@##
答案:B解析:平面π的法向量所求直线的方向向量为i+k,故应选B。@##
-
第14题:
曲面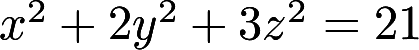 在点
在点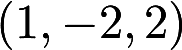 的法线方程为答案:解析:
的法线方程为答案:解析:
-
第15题:
曲面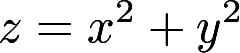 与平面
与平面  平行的切平面的方程是答案:解析:
平行的切平面的方程是答案:解析:
-
第16题:
设直线L过A(1,0,0),B(0,1,1)两点,将L绕z轴旋转一周得到曲面∑,∑与平面z=0,z=2所围成的立体为Ω.
(Ⅰ)求曲面∑的方程;
(Ⅱ)求Ω的形心坐标.答案:解析:【分析】利用定义求旋转曲面∑的方程;利用三重积分求Ω的形心坐标.
-
第17题:
已知平面π过点M1(1,1,0),M2(0,0,1),M3(0,1,1),则与平面π垂直且过点(1,1,1)的直线的对称方程为:
 答案:A解析:提示 求出过M1,M2,M3三点平面的法线向量。
答案:A解析:提示 求出过M1,M2,M3三点平面的法线向量。

@## -
第18题:
已知平面π过点(1,1,0)、(0,0,1), (0,1,1),则与平面π垂直且过点(1,1,1)的直线的对称式方程为( )。 答案:B解析:正确答案是B。
答案:B解析:正确答案是B。
提示:平面π的法向量 ,所求直线的方向向量为i+k ,故应选B。
,所求直线的方向向量为i+k ,故应选B。 -
第19题:
过原点且与平面2x-y+3z+5=0平行的平面方程为______.答案:解析:已知平面的法线向量n1=(2,-1,3),所求平面与已知平面平行,因此可取所求平面的法线向量n=n1=(2,-1,3),又平面过原点(0,0,0),由平面的点法式方程可知,所求平面方程为
-
第20题:
已知直线经过(x1,y1)点,斜率为k(k≠0),则直线方程为y=2kx+2。
正确答案:错误 -
第21题:
APT自动编程语句中,如下()等方法可以定义圆。
- A、圆心和半径
- B、已知不共线三点
- C、过已知点平行于已知平面
- D、平面方程
- E、圆心和切线
正确答案:A,B,D -
第22题:
填空题过x轴和点(1,-1,2)的平面方程为____。正确答案: 2y+z=0解析:
由于所求平面经过x轴,故可设其方程为By+Cz=0。又由于所求平面经过点(1,-1,2),故其满足平面方程,得-B+2C=0,即B=2C。故所求平面方程为2Cy+Cz=0,即2y+z=0。 -
第23题:
填空题过点P(-1,2)且与圆(x+5)2+(y-5)2=25相切的直线方程为____.正确答案: 4x-3y+10=0解析:
易知点P在圆上,故所求切线方程为[(-1)+5](x+5)+(2-5)(y-5)=25,即4x-3y+10=0.
