itgle.com

用递归是可以定义语言的。如表述命题逻辑的一种语言可以如下定义： （1)一个命题是其值为真或假的一个判断语句； （2)如果X是一个命题，Y也是一个命题，则X and Y，X or Y, not X也是一个命题； （3)如果X是一个命题，则（X)也是一个命题，括号内的命题运算优先； （4)命题由以上方式构造。 若X，Y，Z，M等均是一个命题，问不符合上述递归定义的语句是_____。A．(X and Y not Z)B．XC．(X)D．((X and Y) or (not Z)) and (not M)

题目

用递归是可以定义语言的。如表述命题逻辑的一种语言可以如下定义： （1)一个命题是其值为真或假的一个判断语句； （2)如果X是一个命题，Y也是一个命题，则X and Y，X or Y, not X也是一个命题； （3)如果X是一个命题，则（X)也是一个命题，括号内的命题运算优先； （4)命题由以上方式构造。 若X，Y，Z，M等均是一个命题，问不符合上述递归定义的语句是_____。

A．(X and Y not Z)

B．X

C．(X)

D．((X and Y) or (not Z)) and (not M)

相似考题

1.A={x|x＜100且为质数}，在A上定义*和.如下：x*y=max(x，y)，x.y=LCM(x,y)，x，y∈A，这里LCM(x,y)表示x与y的最小公倍数，则下面命题正确的是Ⅰ．＜A，*＞构成代数系统：Ⅱ．＜A，.＞构成代数系统；A．只有ⅠB．只有ⅡC．Ⅰ和ⅡD．没有

2.当一个联言命题为真时,意味着它的每个联言肢都(),若一个联言命题中有一个肢命题假,该联言命题就()。

3.定义：①全概率命题是其真实性的概率为100%的命题。②大概率命题是其真实性概率较高，通常在50%以上的命题。③辩证命题是著联言命题的两个支命题都是条件命题，而这两个联言支的后设彼此之间具有才盾或反对关系。典型例证：(1)人要吃东西才能长期生存(2)如果被害者的财物完整无缺，则凶手作案的动机就不是图财害命(3)他既是一个高个子，又是一个矮个子上述典型与定义存在对应关系的数目有（ ）。A．O个B．1个C．2个D．3个

4.设A为一个命题,对于任意一个命题B而言,若要使"只有A,才B"为真,则A的真假值必须是()。A、真值B、假值C、真值或者假值D、真值并且假值

参考答案和解析
B
更多“用递归是可以定义语言的。如表述命题逻辑的一种语言可以如下定义： （1)一个命题是其值为真或假的一个判断语句； （2)如果X是一个命题，Y也是一个命题，则X and Y，X or Y, not X也是一个命题； （3)如果X是一个命题，则（X)也是一个命题，括号内的命题运算优先； （4)命题由以上方式构造。 若X，Y，Z，M等均是一个命题，问不符合上述递归定义的语句是_____。”相关问题

  • 第1题：

    判断下列命题是真命题还是假命题，如果是假命题，举出一个反例。

    （1）两个锐角的和是锐角；

    （2）邻补角是互补的角；

    （3）同旁内角互补。


    （1）假命题（∠A=40°,∠B=50°， ∠A+∠B=90°）

    （2）真命题

    （3）假命题（作图可知）


  • 第2题：

    定义： （1）全概率命题是其真实性的概率为100%的命题。

    （2）大概率命题是其真实性概率较高，通常在50%以上的命题。

    （3）辨证命题是若联言命题的两个支命题都是条件命题，而这两个联言支的后设彼此之间具有矛盾或反对关系。

    典型例证： （1）人要吃东西才能长期生存。

    （2）如果被害者的财物完整无缺，则凶手作案的动机就不是图财害命。

    （3）他既是一个高个子，又是一个矮个子。（ ）

    A.0个

    B.1个

    C.2个

    D.3个


    正确答案：D
    83.【答案】D。例证（1）是全概率命题，例证（2）是大概率命题，例证（3）是辩证命题，应选D。

  • 第3题：

    A={x，x＜100且为质数}，在A上定义*和.如下： x*y=max(x，y)，x.y=LCM(x，y)， 这里LCM(x，y)表示x与y的最小公倍数，则下面命题正确的是( )。

    Ⅰ．＜A，*＞构成代数系统

    Ⅱ．＜A，.＞构成代数系统

    A．只有Ⅰ

    B．只有Ⅱ

    C．Ⅰ和Ⅱ

    D．没有


    正确答案：A

  • 第4题：

    下列命题中，假命题为( )。
    A．存在四边相等的四边形不是正方形
    B．z1，z2∈C，zl=z2为实数的充分必要条件是z1+z2互为共轭复数
    C．若X，Y∈R，且x+y>2，则X，Y至少有一个大于1
    D．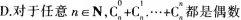


    答案：B
    解析：
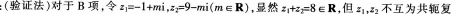    数，故B为假命题，应选B。

  • 第5题：

    充分条件指的是对于两个命题X和Y，当X成立时，则Y成立，那么X是Y的充分条件；必要要条件指的是对于两个命题X和Y，当X不成立时，则Y不成立，那么X是Y的必要条件。
    根据上述定义，下列哪项中X是Y的必要条件？

    A.X：该数能被6整除；Y：该数能被2整除
    B.X：该数能被6整除；Y：该数能被4整除
    C.X：该数能被3整除；Y：该数能被6整除
    D.X：该数能被4整除；Y：该数能被3整除

    答案：C
    解析：
    本题考查“必要条件”的定义。
    其关键信息为：当X不成立时，则Y不成立。
    A项，当一个数不能被6整除时，无法得到该数不能被2整除，比如“4”，不符合定义，故A项错误，排除。
    B项，当一个数不能被6整除时，无法得到该数不能被4整除，比如“4”，不符合定义，故B项错误，排除。
    C项，因为6可以被分解为2×3，所以不能被3整除，就一定就不能被6整除，符合定义，故C项正确，当选。
    D项，当一个数不能被4整除时，无法得到该数不能被3整除，比如“6”，不符合定义，故D项错误，排除。
    故本题的正确答案为C项。

  • 第6题：

    在命题逻辑中，依据一个复合命题所带的联结词的不同，复合命题的类别可以分为（）

    A假言命题

    B联言命题

    C选言命题

    D负命题

    E直言命题


    A,B,C,D
    略

  • 第7题：

    一个直言命题的主项不周延，则这个命题的量是（）。一个直言命题的谓项不周延，则它的质是（）。


    正确答案:特称的；肯定的

  • 第8题：

    下列语句作为“复合命题”的定义或划分是否正确？为什么？ “复合命题就是包含两个以上简单命题的命题。它可以分为假言命题、选言命题和联言命题。”


    正确答案:作为定义和划分均不正确；
    作为定义，犯了“定义过窄”的错误；
    作为划分，犯了“划分不全”的错误。

  • 第9题：

    条件命题是指一个命题为真是另一个命题为真的充分条件的命题。（）


    正确答案:正确

  • 第10题：

    填空题
    一个联言命题只要有一个联言支为（），则该联言命题就是假的；只有当联言支（）时，联言命题才真。

    正确答案： 假,都为真
    解析： 暂无解析

  • 第11题：

    单选题
    若E(X)，E(Y)都存在，则下面命题中错误的是 ( )
    A

    E(X+y)=E(X)+E(y)

    B

    E(X - Y)=E(X) - E(Y)

    C

    E(6X)=6E(X)

    D

    E(Xy)=E(X)E(y)


    正确答案： D
    解析： 暂无解析

  • 第12题：

    填空题
    如果三段论的前提中有一个否定命题，则它的结论应是（）命题。如果前提中有一个特称命题，则它的结论应是（）命题。

    正确答案： 肯定,特称
    解析： 暂无解析

  • 第13题：

    命题p:不经过第一象限的图象所对应的函数一定不是幂函数.命题q:函数y=x+2/x的单调递增区间是[-√2,0)∪[√2,+∞), 则下列命题中,真命题是( ).

    (A)p∧q.

    (B)(￢p)∨q.

    (C)(￢p)∧(￢q).

    (D)p∧(￢q).


    参考答案D

  • 第14题：

    设L(x): x是演员，J(x): x是老师，A(x，y): x佩服y，那么命题“所有演员都佩服某些老师”符号化为(61)。

    A．

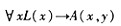
    B．

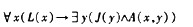
    C．

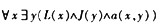
    D．


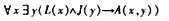    正确答案：D
    解析：将命题符号化为“”。故应选择(D)。注意：符号化为“”是不对的，它的意义是所有演员和某些老师，x佩服y。

  • 第15题：

    如果函数f(x，y)在(0，0)处连续，那么下列命题正确的是


    答案：B
    解析：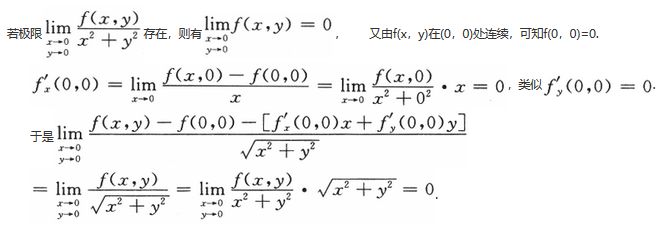

    由微分定义知f(x，y)在(0，0)处可微，故应选(B).【评注】1.本题主要考查二元函数连续、偏导数、可微的定义.
    2.可采用举反例排除错误答案.取f(x，y)=｜x｜+｜y｜排除(A)，f(x，y)=x+y排除(C)、(D).

  • 第16题：

    有四个三角函数命题：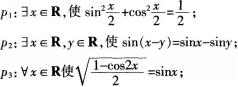
    p4：若sinx=cosy。则x+y=π/2。其中假命题个数为( )。

    A、0
    B、1
    C、2
    D、3

    答案：D
    解析：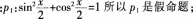

  • 第17题：

    命题“若x≤-2，则x2≥4”的逆否命题是( )。

    A.若X2≤4，则x≥一2
    B.若x2<4，则x>-2
    C.若x2≥4，则x≤-2
    D.若x2>4，则x<-2

    答案：B
    解析：
    原命题为“若P，则q”，则逆否命题为“若非q，则非P”。即为“若x2<4，则x>-2”。

  • 第18题：

    对于“李××是法官”和“李××不是法官”这两个命题（）。

    • A、如果同时断定它们都真，就违反了矛盾律
    • B、如果同时断定它们都假，就违反了排中律
    • C、如果断定其中一个命题为真另一个命题为假，就违反了同一律
    • D、如果根据其中一个命题假推论出另一个命题真，就违反了充足理由律
    • E、既不断定其中一个命题真也不断定其中另一个命题假，这样并不违反逻辑思维规律

    正确答案:A,B,D

  • 第19题：

    如果三段论的前提中有一个否定命题，则它的结论应是（）命题。如果前提中有一个特称命题，则它的结论应是（）命题。


    正确答案:肯定；特称

  • 第20题：

    下列命题中，假命题为（）。

    • A、存在四边相等的四边形不是正方形
    • B、z1，z10∈C，为实数的充分必要条件是z1、z2互为共轭复数
    • C、若x，y∈R，且x+y>2，则x，y至少有一个大于1
    • D、对于任意n∈N，Cn0+Cn1，…+Cnn：都是偶数

    正确答案:B

  • 第21题：

    一个联言命题只要有一个联言支为（），则该联言命题就是假的；只有当联言支（）时，联言命题才真。


    正确答案:假；都为真

  • 第22题：

    多选题
    在命题逻辑中，依据一个复合命题所带的联结词的不同，复合命题的类别可以分为（）
    A

    假言命题

    B

    联言命题

    C

    选言命题

    D

    负命题

    E

    直言命题


    正确答案： A,C
    解析： 暂无解析

  • 第23题：

    多选题
    对于“李××是法官”和“李××不是法官”这两个命题（）。
    A

    如果同时断定它们都真，就违反了矛盾律

    B

    如果同时断定它们都假，就违反了排中律

    C

    如果断定其中一个命题为真另一个命题为假，就违反了同一律

    D

    如果根据其中一个命题假推论出另一个命题真，就违反了充足理由律

    E

    既不断定其中一个命题真也不断定其中另一个命题假，这样并不违反逻辑思维规律


    正确答案： C,E
    解析： 暂无解析

  • 第24题：

    判断题
    条件命题是指一个命题为真是另一个命题为真的充分条件的命题。（）
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

相关内容