itgle.com

半径r=1m的均质圆盘在粗糙水平地面作纯滚动，其质心加速度为1m/s2,则其角加速度为1rad/s2。

题目

半径r=1m的均质圆盘在粗糙水平地面作纯滚动，其质心加速度为1m/s2,则其角加速度为1rad/s2。

相似考题

1.车轮沿曲面向右滚动,已知车轮半径为R,轮心在某一瞬时的速度为vo,加速度为ao,加速度方向在水平线以下且与速度方向的夹角为β,则车轮的角加速度为acosβ／R。()此题为判断题(对，错)。

2.直角刚杆OAB在图示瞬间角速度ω=2rad/s，角加速度ε=5rad/s2，若OA=40cm，AB=30cm，则B点的速度大小、法向加速度的大小和切向加速度的大小为：A.100cm/s；200cm/s2；250cm/s2 B.80cm/s2；160cm/s2；200cm/s2 C.60cm/s2；120cm/s2；150cm/s2 D.100cm/s2；200cm/s2；200cm/s2

3.质量为m，半径为R的均质圆轮，绕垂直于图面的水平轴O转动，其角速度为w。在图示瞬时，角加速度为0，轮心C在其最低位置，此时将圆轮的惯性力系向O点简化， 其惯性力主矢和惯性力主矩的大小分别为：

4.一重为100kg,半径为1m的均质圆齿轮以10rad／s的速度绕其自身的圆心旋转,则其动量为1000kg.m／s。()此题为判断题(对，错)。

更多“半径r=1m的均质圆盘在粗糙水平地面作纯滚动，其质心加速度为1m/s2,则其角加速度为1rad/s2。”相关问题

  • 第1题：

    均质圆盘重W，半径为R，绳子绕过圆盘，两端各挂重Q和P的物块，绳与盘之间无相对滑动，且不计绳重，则圆盘的角加速度为（　　）。


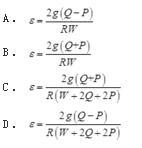    答案：D
    解析：

  • 第2题：

    质量为m1的均质杆OA，一端铰接在质量为m2的均质圆盘中心，另一端放在水平面上，圆盘在地面上作纯滚动（如图所示）。圆心速度为v，则系统的动能为：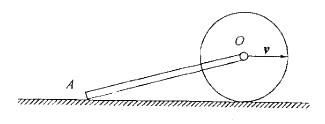



    答案：D
    解析：
    提示：平面运动刚体的动能为1/2mvc2+1/2Jcω2。

  • 第3题：

    图示均质圆轮，质量为m，半径为r，在铅垂图面内绕通过圆盘中心O的水平轴转动，角速度为ω，角加速度为ε，此时将圆轮的惯性力系向O点简化，其惯性力主矢和惯性力主矩的大小分别为（　　）。




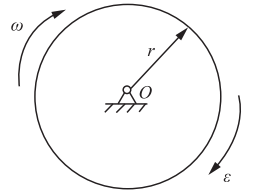
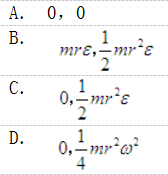    答案：C
    解析：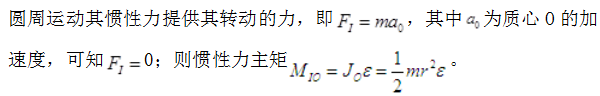

  • 第4题：

    一半径为r的圆盘以匀角速ω在半径为R的圆形曲面上作纯滚动（如图所示）， 则圆盘边缘上图示M点加速度aM的大小为：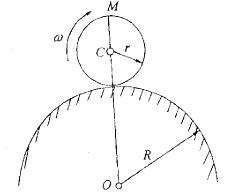



    答案：B
    解析：

  • 第5题：

    直角刚杆OAB可绕固定轴O在图示平面内转动，已知OA=40cm，AB=30cm，ω =2rad/s，α=1rad/s2，则图示瞬时，B点加速度在y方向的投影为：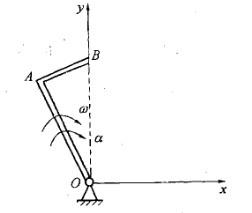

    A. 40cm/s2 B. 200cm/s2 C. 50 cm/s2 D. -200cm/s2


    答案：D
    解析：
    提示:定轴转动刚体，B点的转动半径为OB。

  • 第6题：

    如图4-40所示,直角刚杆中AO = 1m,BO=2m,已知某瞬时A点的速度vA= 3m/s, 而B点的加速度与BO成θ= 60°，则该瞬时刚杆的角加速度为（ ）rad/s2。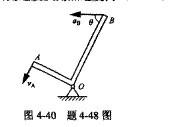


    答案：D
    解析：

  • 第7题：

    半径为R、质量为m的均质圆轮沿斜面作纯滚动如图4-75所示。已知轮心C的速度为V、加速度为a,则该轮的动能为（ ）。

    A. 1/2mv2 B. 3/2mv2 C. 3/4mv2 D. 1/4mv2


    答案：C
    解析：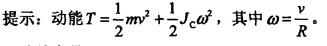

  • 第8题：

    一物体做匀减速直线运动，初速度为10m/s，加速度大小为1m/s2，则物体在停止运动前ls内的平均速度为（）

    • A、5.5m/s
    • B、5m/s
    • C、1m/s
    • D、0.5m/s

    正确答案:D

  • 第9题：

    一物体做匀速直线运动，初速度大小为10m/s，加速度在1m/s2，则物体在停止运动前2s内的平均速度大小为（）

    • A、0.5m/s
    • B、1m/s
    • C、5m/s
    • D、5.5m/s

    正确答案:B

  • 第10题：

    一物体做匀减速直线运动，初速度大小为10m/s，加速度大小为1m/s2，则物体在停止运动前2s内的平均速度大小为（）

    • A、0.5m/s
    • B、1m/s
    • C、5m/s
    • D、5.5m/s

    正确答案:B

  • 第11题：

    一物体在做匀加速直线运动，第2s内的平均速度为1m/s，第7s内的位移为6m，则该物体的加速度为（）

    • A、1m/s2
    • B、2m/s2
    • C、3m/s2
    • D、4m/s2

    正确答案:A

  • 第12题：

    某一时刻动点的速度为2m/s，曲率半径为1m，则此时法向加速度的大小等于（）

    • A、4m/s2
    • B、2m/s2
    • C、8m/s2
    • D、6m/s2

    正确答案:A

  • 第13题：

    半径R=10cm的鼓轮，由挂在其上的重物带动而绕O轴转动，如图所示。重物的运动方程为x= 100t2（x以m计，t以s计）。则鼓轮的角加速度α的大小和方向是: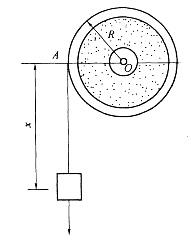


    A.α=2000rad/s2，顺时针向
    B. α==2000rad/s2，逆时针向
    C.α=200rad/s2，顺时针向
    D. α==200rad/s2，逆时针向

    答案：B
    解析：
    提示：重物的加速度即是轮缘的切向加速度。

  • 第14题：

    偏心轮为均质圆盘，其质量为m，半径为R，偏心距OC=R/2。若在图示位置时，轮绕O轴转动的角速度为ω，角加速度为α，则该轮的惯性力系向O点简化的主矢FI和主矩MIO的大小为：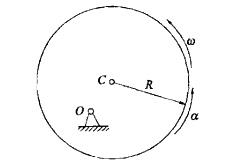



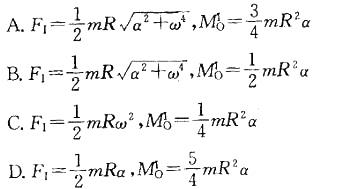    答案：A
    解析：
    提示：MIO=-JOα，其中 JO = JC + m* OC2 。

  • 第15题：

    半径为R、质量为m的均质圆轮沿斜面做纯滾动如图所示。已知轮心C的速度为v、加速度为a，则该轮的动能为：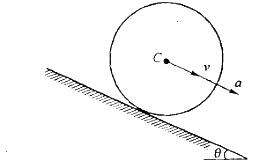



    答案：C
    解析：

  • 第16题：

    如图所示，曲柄OA长R，以匀角速度ω绕O轴转动，均质圆轮B在水平面上做纯滚动，其质量为m，半径为r。在图示瞬时，OA杆铅直。圆轮B对接触点C的动量矩为（　　）mRrω。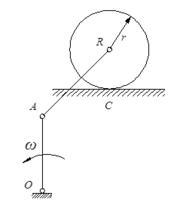

    A．0.5
    B．1.0
    C．1.5
    D．2.0

    答案：B
    解析：
    图示瞬时，点A和点B的速度方向均沿水平方向， AB杆作平动，圆轮B的轮心速度

  • 第17题：

    质量为m，半径为R的均质圆盘，绕垂直于图面的水平轴O转动，其角速度为ω，在图示瞬时，角加速度为零，盘心C在其最低位置，此时将圆盘的惯性力系向O点简化， 其惯性力主矢和惯性力主矩的大小分别为：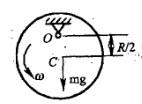



    答案：A
    解析：
    提示：根据定轴转动刚体惯性力系简化的主矢和主矩结果，其大小为FI= mac ; MIO=JOα。

  • 第18题：

    质量为m,半径为R的均质圆盘，绕垂直于图面的水平轴O转动，其角速度为ω，在图4-78示瞬时，角加速度为零，盘心C在其最低位置，此时将圆盘的惯性力系向O点简化，其惯性力主矢和惯性力主矩的大小分别为（）。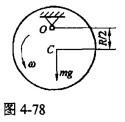



    答案：A
    解析：
    提示：根据定轴转动刚体惯性力系简化的主矢和主矩结果，其大小FI=maC，MIO=JOα。

  • 第19题：

    如图4-72所示，质量为m1的均质杆OA, 一端较接在质量为m2的均质圆盘中心， 另一端放在水平面上，圆盘在地面上作纯滚动。圆心速度为v,则系统的动能为（ ）。



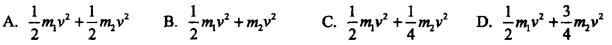    答案：D
    解析：
    提示：杆OA平行移动，轮O作平面运动，分别根据动能的定义求解。

  • 第20题：

    甲、乙两物体的加速度分别为a1=1m/s2、a2=-1m/s2。则（）

    • A、甲物体的速度增加了1m/s
    • B、乙物体的速度减少了1m/s
    • C、甲物体比乙物体的速度变化快
    • D、两物体的速度变化快慢相同

    正确答案:D

  • 第21题：

    两个在同一直线上运动的物体，甲的加速度为1m/s2，乙的加速度是－2m/s2，则（）

    • A、甲的加速度比乙的加速度大
    • B、甲做加速运动，乙做减速运动
    • C、乙的加速度比甲的加速度大
    • D、甲、乙的加速度方向相反

    正确答案:C,D

  • 第22题：

    飞机的起飞过程是从静止出发，在直跑道上加速前进，等达到一定速度时离地．已知飞机加速前进的路程1600m，所用的时间为40s．假设这段运动为匀加速直线运动，用a表示加速度，v表示离地时的速度，则（）

    • A、a＝2m/s2，v＝80m/s
    • B、a＝1m/s2，v＝40m/s
    • C、a＝2m/s2，v＝40m/s
    • D、a＝1m/s2，v＝80m/s

    正确答案:A

  • 第23题：

    用力F1单独作用于某一物体上可产生加速度为3m/s2，力F2单独作用于这一物体可产生加速度为1m/s2，若F1、F2同时作用于该物体，可能产生的加速度大小为（）

    • A、1m/s2
    • B、1.5m/s2
    • C、3m/s2
    • D、5m/s2

    正确答案:C

  • 第24题：

    一质点从静止出发沿半径R=1m的圆周运动，其角加速度随时间t的变化规律是（），则质点的角速度（）


    正确答案:12t2-6t；4t3-3t2 (rad/s)

相关内容