itgle.com

一个袋子里放着各种颜色的小球，其中红球占1/4，后来又往袋子里放了10个红球，这时红球占总数的2/3，问原来袋子里有多少个球？（ ）A．8B．12C．16D．20

题目

一个袋子里放着各种颜色的小球，其中红球占1/4，后来又往袋子里放了10个红球，这时红球占总数的2/3，问原来袋子里有多少个球？（ ）

A．8

B．12

C．16

D．20

相似考题

1.袋子里装有红、蓝两色的小球各12个，先从袋子中拿出一个球，然后将它放回袋子中，混合后再从中拿出一个小球。那么两次抽中不同颜色的小球的几率有（ ）。A．20%B．25%C．50%D．60%

2.有一个袋子里装有红、白、黑三种颜色的球，共100只。 甲说：“袋子里至少有一种颜色的球少于34只。” 乙说：“袋子里至少有一种颜色的球不少于33只。” 丙说：“袋子里任何两种颜色的球的总和不超过99只。” 以下哪项结论成立?（ ） A．甲、乙、丙的看法都正确 B．甲和丙的看法正确，乙的意见不正确 C．乙和丙的看法正确，甲的看法不正确 D．甲和乙的看法正确，丙的看法不正确

3.一个袋子里装了各种颜色的小球，其中红球个数占1/4，后来又向袋子中放入10个红球，这时红球个数占总数的2/3，问原来袋子中共有多少球?

4.袋子里红球与白球的数量之比为19:13，放入若干个红球后，红球与自球的数量之比变为5:3，再放入若干个白球后，红球与白球的数量之比为13:11，已知放入的红球比白球少80个。那么原来袋子里共有多少个球?A．650B．720C．840D．960

更多“一个袋子里放着各种颜色的小球,其中红球占1／4,后来又往袋子里放了10个红球,这时红球占总 ”相关问题

  • 第1题：

    有红、蓝两种颜色的小球若干个，将红球的1/3与蓝球的1/4装入A盒，将红球的2/5与蓝球的3/5装入B盒，这时还剩下18个小球，那么共有小球多少个?（ ）

    A．80

    B．85

    C．90

    D．95


    正确答案：B

  • 第2题：

    一个袋子里放着各种颜色的小球，其中红球占 1/4。后来又往袋子里放了 10 个红球，这时红球占总数的 2/3，问原来袋子里有球多少个？( )

    A.8

    B.6

    C.4

    D.2


    正确答案：A

  • 第3题：

    一个袋子里面有红、黄、蓝三种颜色的球共450个，三个颜色的小球数目比例为2：3：4，问数目最多的颜色的球有多少个?( )

    A.100

    B．150

    C．200

    D．250


    正确答案：C

  • 第4题：

    一个袋子里有10个小球，其中4个白球，6个黑球，无放回地每次抽取1个，则第二次取到白球的概率是多少？（ ）


    答案：D
    解析：

  • 第5题：

    一个袋子里放有10个小球(其中4个白球，6个黑球)，无放回地每次抽取1个，则第二次取到白球的概率是（ ）

    A. 2/15
    B. 4/15
    C. 1/5
    D. 2/5

    答案：D
    解析：
    解题指导： 第一次取到白球，第二次取到白球的机率为4/10*3/9=2/15 ；第一次取到黑球，第二次取到白球的机率为6/10*4/9=4/15 。可知，第二次取到白球的机率为4/15+2/15=2/5,故答案为D。

  • 第6题：

    盒子里有红、黄、绿三种颜色的大小相等的球，其中红球有7个，黄球有5个，从盒中任意拿出一个球，拿到黄球的可能性为，问拿到绿球的可能性是：
    A1/3
    B1/4
    C1/7
    D1/5


    答案：D
    解析：

  • 第7题：

    三个相同的盒子里各有2个球，其中一个盒子里放了2个红球，一个盒子里放了2个蓝球，一个盒子里放了红球和蓝球各1个。随机选择一个盒子后从中随机摸出一球是红球，则这个盒子里另一个球是红球的概率为（ ）。

    A.1/2
    B.3/4
    C.2/3
    D.4/5

    答案：C
    解析：

  • 第8题：

    袋子中有70个红球，30个黑球，从袋中任意摸出一个球，观察颜色后放回袋中，再摸第二个球，观察颜色后也放回袋中。

    （1）求两次摸球均为红球的概率；（3分）

    （2）求两次摸球颜色不同的概率。（4分）


    答案：
    解析：
    本题主要考查的是熟练运用分步法、分类法等方法求概率。

    通过不同事件随机发生概率进行分步分类计算。

  • 第9题：

    袋子中有70个红球，30个黑球，从袋子中连续摸球两次，每次摸一个球，而且是不放回的摸球：

    （1）求两次摸球均为红球的概率。

    （2）若第一次摸到红球，求第二次摸到黑球的概率。


    答案：
    解析：
    本题主要考查求解随机事件的概率方法。

    （1）利用概率近似等于频率，根据相互独立性，可求解两次摸球都是红球的概率。

    （2）由于第一次摸到红球，从剩余的99个球中摸一个黑球，共有30种可能。

  • 第10题：

    盒子里有红、黄、绿三种颜色的大小相等的球，其中红球有7个，黄球有5个，从盒中任意拿出一个球，拿到黄球的可能性为1/3，问拿到绿球的可能性是多少?

    • A、1/3 
    • B、1/4 
    • C、1/7 
    • D、1/5

    正确答案:D

  • 第11题：

    单选题
    袋子中有3个白球，2个红球，1个黄球，现从袋子中随意取2个球，则取得的2个球中1个是红球1个是白球的概率为（）
    A

    1/5

    B

    2/5

    C

    1/3

    D

    2/3


    正确答案： B
    解析： 暂无解析

  • 第12题：

    单选题
    袋子里红、黄、蓝、白四种颜色的球分别有3、4、5、6只，每次只能取出一只球，取出的球不再放回袋子，则至少要取多少次才能保证取出两只红球？（）
    A

    12

    B

    15

    C

    16

    D

    17


    正确答案： C
    解析： 考虑最差情况，先取出白、蓝、黄三种颜色的球，最后取出两个红色的球，要取6+5+4+2=17次。

  • 第13题：

    一个袋子里面红球和白球的比例为2：5，又往袋子里面加入2个红球，结果比例变为1：2，那么袋子里原有多少个红球？（ ）

    A．10

    B．20

    C．28

    D．8


    正确答案：D
    假设原来袋子中红球和白球的总数为2，则红球数原为2/7χ，加入2个红球后，红球数为(2/7χ+2)，总球敬为(χ+2)，可列一方程式：2/7χ+2=(χ+2)/3，可以解知χ=28，则红球即为28×2/7=8个。

  • 第14题：

    盒子中装了大球和小球，颜色分别有红色和白色。大球中红球占80%，小球中红球占602，在整个盒子里红球占62%，红色大球与白色小球数目之比是（ ）。

    A．1：9

    B．9：1

    C．2：9

    D．9：2


    正确答案：C

  • 第15题：

    袋子里有20个乒乓球，其中20个黄球，30个白球。现在两个人依次不放回地从袋子中取出一个球，第二个人取出黄球的概率是( )

    A.1/5

    B.3/5

    C.2/5

    D.4/5


    正确答案：C

  • 第16题：

    一个袋子里有5个球，其中有2个红球。从袋子里拿2个球，拿到红球的概率有多大?

    A. 50%
    B. 60%
    C. 70%
    D. 80%

    答案：C
    解析：
    （C21C31+C12）/C52=(6+1)10=70%。故答案为C。

  • 第17题：

    袋子里有6个红球和4个白球，随机取出3个球，问取出的球中红球不超过一个的概率最接近以下哪个？

    A.0.1
    B.0.2
    C.0.3
    D.0.4

    答案：C
    解析：
    第一步，本题考查概率问题，属于分类分步型。

  • 第18题：

    一个袋子里放着各种颜色的小球，其中红球占1/4，后来又往袋子里放了10个红球，这时红球占总数的2/3，问原来袋子里有多少个球？（）


    A. 8
    B. 12
    C. 16
    D. 20

    答案：A
    解析：
    解题指导： 设原来袋中有X个球，则一开始红球有1/4X个，根据题意可得方程1/4X+10=2/3（X+10），解得X=8，故答案选A。

  • 第19题：

    一个袋子里面有10个球,包括红球、白球和黑球。已知从袋中任意摸一个球，得到黑球 的概率是2/5，从袋中任意摸两个球,至少有一个是白球的概率是7/9，问袋子里有多少个红球？

    a.l b.2 c.3 d.4


    答案：A
    解析：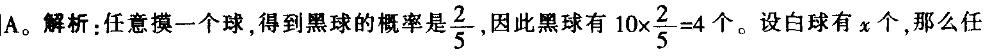

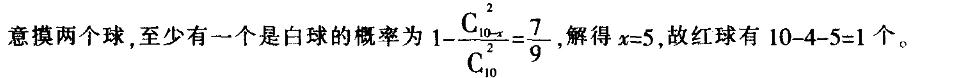
  • 第20题：

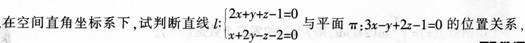
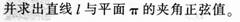    袋子中有70个红球，30个黑球，从袋子中连续摸球两次，每次摸一个球，且第一次摸出的球，不放回袋中：
    (1)求两次摸球均为红球的概率：
    (2)若第一次摸到红球，求第二次摸到黑球的概率。


    答案：
    解析：
    平面π的法向量为n=(3，-1，2)；

  • 第21题：

    袋子中有3个白球，2个红球，1个黄球，现从袋子中随意取2个球，则取得的2个球中1个是红球1个是白球的概率为（）

    • A、1/5
    • B、2/5
    • C、1/3
    • D、2/3

    正确答案:B

  • 第22题：

    一个袋子中有5个球：两个绿的，一个红的，两个白的。要从袋子中拿出一个球。拿出一个红球、绿球和白球的总概率是多少？（） （假设球拿出后会还回去。）

    • A、1
    • B、5分之1
    • C、5分之3
    • D、5分之2

    正确答案:A

  • 第23题：

    单选题
    一个袋子中有5个球：两个绿的，一个红的，两个白的。要从袋子中拿出一个球。拿出一个红球、绿球和白球的总概率是多少？（） （假设球拿出后会还回去。）
    A

    1

    B

    5分之1

    C

    5分之3

    D

    5分之2


    正确答案： A
    解析： 所有随机变量的值之和一定等于1。

相关内容