在一次围棋比赛中，实行单循环制(即每个选手都与其他选手比赛一局)，每局胜者记2分，输者记0分，如果平局则双方各得1分。今有四位记分员统计了比赛中全部选手的得分总和，结果分别为2005、2004、2070、2008，经核实只有一位记分员统计无误。问这次比赛共有多少名选手参加?（ ） A．44 B．45 C．46 D．47

解法一：第一步，题目难度较大，无从入手，考虑使用代入排除法解题，代入验证时采用就简代入原则，优先从D选项10开始代入。第二步，若参加比赛的男选手为10人，则参加比赛的女选手为1人，共11人。每场比赛无论是分出胜负还是平局，均共得2分，11人参加循环赛共进行＝55场比赛，得分总数应该为55×2＝110分，男选手得分是女选手的4.5倍，则女选手共得110÷5.5＝20分。1名女选手共参加10场比赛，如果都获胜恰好得20分，满足题意。因此，选择D选项。解法二：设女选手有x人，则男选手有10x人，共有选手11x人。进行循环赛共有



场，每场比赛无论是分出胜负还是平局，均共得2分，因此循环赛总分数为（



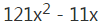
）分。男生所得分数是女生的4.5倍，则女生所得分数为



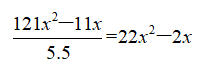
分。一个女生共进行11x－1场比赛，最多得22x－2分，则22x2－2x≤22x－2，解不等式得x≤1，则最多有1名女选手，10名男选手。因此，选择D选项。

很容易判断比赛总分不可能为奇数，则总分只可能是1980，那么由1980/2=990，所以共进行了990场比赛，设参赛选手为X，(x-1)+(x-2)+...+2+1=990，解得X=45，故答案为B。

单循环赛，每人赛9盘棋，所以最高分为9分，前两名都没有输，说明没有全胜的人。所以，最高分最多为8. 5分。
那么，第二名最多8分，第三名最多8.5+8-10 = 6. 5（分），第四名最多6分。
后四名选手之间要赛4X3 /2=6（盘）。
每盘出现1分，这四人之间要累计6分，那么这四人的总分至少要有6分，就是说第四名的分数至少是6分。
综合“第四名最多6分”“第四名的分数至少是6分”，可知第四名的得分应该是6分。
由此可知：第三名6. 5分，第四名6分，第一名是8. 5分，第二名是8分，后四人最后总分是6分。
10名选手的循环赛总盘数是1/2x10x(10-1)=45(盘)，总分是1x45 = 45(分)。故第一到第六名共得的分数为45-6=39(分)。所以本题选D。

概率问题。分析甲获胜的情况可得：所求概率=0.8×0.8+0.8×0.2×0.8+0.2×0.8×0.8=0.896。因此，本题答案为C选项。