有62 名学生,会击剑的有 11 人,会游泳的有 56 人,两种都不会的有 4人,问两种都会的学生有多少人?( )A.1 人B.5 人C.7 人D.9 人
题目
有62 名学生,会击剑的有 11 人,会游泳的有 56 人,两种都不会的有 4人,问两种都会的学生有多少人?( )
A.1 人
B.5 人
C.7 人
D.9 人
相似考题
更多“有62 名学生,会击剑的有 11 人,会游泳的有 56 人,两种都不会的有 4人,问两种都会的学生有多少 ”相关问题
-
第1题:
一个班里有30名学生,有12人会跳拉丁舞,有8人会跳肚皮舞,有10人会跳芭蕾舞。问 至多有几人会跳两种舞蹈?( )A. 12 人
B. 14 人
C. 15 人
D. 16 人答案:C解析:根据三集合容斥原理公式: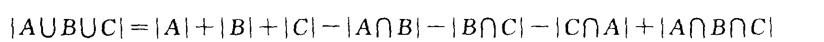
要求会跳两种舞蹈的人最多,则需要让所有会跳舞的人都会两种舞蹈,此时会跳两种舞蹈的人数为(12 + 8 + 10)÷2=15(人)。具体构造如下:会跳拉丁的12人中有7人会拉丁和芭蕾,5人会拉丁和肚皮,这时有12 人会跳两种舞蹈;剩下的3个人都会芭蕾和肚皮两种舞蹈,此时共有12 + 3 = 15(人)会两种舞蹈。 -
第2题:
某班56名学生参加了奥数或作文课外兴趣小组的活动,其中参加奥数的有32人,参加作文的有35人,问两种活动都参加的有多少人?()A. 3
B. 11
C. 21
D. 24答案:B解析:两种活动都参加得人有32+35-56=11人。故答案为B。 -
第3题:
某单位有青年员工85人,其中68人会骑自行车,62人会游泳,既不会骑车又不会游泳的有12人,则既会骑车又会游泳的有多少人?( )A. 57人
B. 73人
C. 130人
D. 69人答案:A解析:用集合法68+62+12-85=57。故答案为A。 -
第4题:
某班在筹备联欢会时发现很多同学都会唱歌和乐器演奏,但有部分同学这2种才艺都不会。具体有4种情况:只会唱歌,只会乐器演奏,唱歌和乐器演奏都会,唱歌和乐器演奏都不会。现知会唱歌的有22人,会乐器演奏的有15人,两种都会的人数是两种都不会的5倍。这个班至多有( )人。A.27
B.30
C.33
D.36答案:C解析:第一步,本题考查容斥问题,属于二集合容斥类。
第二步,设该班共有x人,唱歌和乐器演奏都不会的有y人,则两种都会的有5y人,根据二集合容斥公式可得:x-y=22+15-5y,化简得:x=37-4y。
第三步,要使x最大,则y应最小,当y=1时,x=33,故这个班至多有33人。 -
第5题:
有 62 名学生,会击剑的有 11 人,会游泳的有 56 人,两种都不会用的有 4 人,问两种都 会的学生有多少人?
A.1 人 B。5 人 C、7 人 D. 9 人答案:D解析:此题简单,直接可列式求结果,即56+11-(62-4)=9人。故选D。
