itgle.com

有17人分4组进行蛇形进位，那么第4组有_______人，他们分别是_______号选手。

题目

有17人分4组进行蛇形进位，那么第4组有_______人，他们分别是_______号选手。

相似考题

1.在一次象棋比赛中；共有n名选手参加，每位选手都与其他选手恰好比赛一局。每局比赛胜者得2分，负者得0分，平局两位选手各得l分。今有四位同学统计了全部选手的得分总和，分别是238，239，240，242，经核实只有一位同学的统计数据是正确的，正确的数据是（ ）。 A．238 B．239 C．240 D．242

2.把一些书分给几名同学，如果每人分3本，那么余8本；如果前面的每名同学分5本，那么最后一人就分不到3本。这些书有多少本？共有多少人？

3.请教:2010年村官《行测职业能力测验》专家命题预测试卷(2)第2大题第6小题如何解答?【题目描述】第 31 题某校参加“祖冲之杯”数学邀请赛的选手平均分数是75分，其中参赛男选手比女选手人数多80%，而女选手比男选手的平均分数高202，则女选手的平均分是多少?（　）

4.一次象棋比赛共有10名选手参加，他们分别来自甲、乙、丙三个队，每个人都与其余九名选手各赛一盘，每盘棋的胜利者得1分，负者得0分，平局各得0.5分。结果甲队选手平均得4.5分，乙队选手平均得3.6分，丙队选手平均得9分，那么甲、乙、丙三队参加比赛的选手的人数依次是（ ）。A. 6人、3人、1人B.4人、5人、1人C. 3人、5人、2人D.5人、1人、4人

参考答案和解析
正确答案：4;4,5,12,13
更多“有17人分4组进行蛇形进位，那么第4组有_______人，他们分别是_______号选手。”相关问题

  • 第1题：

    该公司有3个车间，共有流水线操作工人200人，对他们进行工作分析应该（ ）。

    A．对他们进行逐一分析

    B．每人交一份工作日志给其主管进行汇总分析

    C．选择有代表性的工作进行分析

    D．各车间挑选10人进行分析


    正确答案：C

  • 第2题：

    在一次象棋比赛中，每两个选手恰好比赛一局，每局赢者记2分，输者记0分，平局每个选手各记1分。今有4个人统计这次比赛中全部得分的总数，由于有人粗心，其数据各不相同，分别为1979、1980、1984、1985，经核实，其中有一人统计无误，则这次比赛共有多少名选手参加

    A.42
    B.44
    C.45
    D.47

    答案：C
    解析：
    设有n名选手参加，则共比赛了



    局，共得



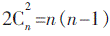
    分，4个人统计的数中，只有1980＝45×44，可写成n（n－1）的形式。故n＝45，这次比赛共有45名选手参加。

  • 第3题：

    象棋比赛中，每个选手都与其他选手恰好比赛一局，每局胜者记2分，负者记0分，和棋各记1分，四位观众统计了比赛中全部选手得分总数分别是:1979，1980，1983，1985，经核实只有一位观众统计正确，则这次比赛的选手共有多少名?

    A. 44
    B. 45
    C. 46
    D. 47

    答案：B
    解析：
    很容易判断比赛总分不可能为奇数，则总分只可能是1980，那么由1980/2=990，所以共进行了990场比赛，设参赛选手为X，(x-1)+(x-2)+...+2+1=990，解得X=45，故答案为B。

  • 第4题：

    某单位举行象棋比赛，计分规则为：赢者得2分，负者得0分，平局各得1分，每位选手与其他选手各下一局。已知男选手数是女选手的10倍，而得分是女选手的4.5倍，则参加比赛的男选手数是

    A.40人
    B.30人
    C.20人
    D.10人

    答案：D
    解析：
    解法一：第一步，题目难度较大，无从入手，考虑使用代入排除法解题，代入验证时采用就简代入原则，优先从D选项10开始代入。第二步，若参加比赛的男选手为10人，则参加比赛的女选手为1人，共11人。每场比赛无论是分出胜负还是平局，均共得2分，11人参加循环赛共进行＝55场比赛，得分总数应该为55×2＝110分，男选手得分是女选手的4.5倍，则女选手共得110÷5.5＝20分。1名女选手共参加10场比赛，如果都获胜恰好得20分，满足题意。因此，选择D选项。解法二：设女选手有x人，则男选手有10x人，共有选手11x人。进行循环赛共有



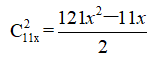
    场，每场比赛无论是分出胜负还是平局，均共得2分，因此循环赛总分数为（



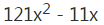
    ）分。男生所得分数是女生的4.5倍，则女生所得分数为



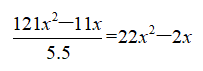
    分。一个女生共进行11x－1场比赛，最多得22x－2分，则22x2－2x≤22x－2，解不等式得x≤1，则最多有1名女选手，10名男选手。因此，选择D选项。

  • 第5题：

    几位同学参加了计箅机考试。如果甲的得分提高17分，则他们的平均分数就达到92分； 如果甲的得分降低3分，则他们的平均分就只有88分。那么,这些同学共有（ ）人。
    A. 3 B. 4 C. 5 D. 6


    答案：C
    解析：
    C [解析]两次假设甲的得分相差17 + 3 = 20(分），而平均分相差92 —88=4(分）， 因此，这些同学共有20÷4 = 5(人）。

  • 第6题：

    各线AFC系统供电方式有以下不同（）

    • A、1号线一期提供专用UPS
    • B、1号线续建、2、5号线不提供专用UPS采用集中UPS供电方式
    • C、1号线一期、2号线没有进行分时间管理
    • D、1号线续建、5号线分1分钟和15分钟UPS供电管理工作
    • E、3号线分5分钟和30分钟UPS供电管理工作

    正确答案:A,B,C,D

  • 第7题：

    网球比赛选手换边有多少时间（）

    • A、45秒
    • B、60秒
    • C、85秒
    • D、2分

    正确答案:C

  • 第8题：

    进行两个补码整数9CH和7AH相加运算后，会产生（）。

    • A、无溢出且无进位
    • B、无溢出但有进位
    • C、有溢出且有进位
    • D、有溢出但无进位

    正确答案:B

  • 第9题：

    单选题
    《WS373-2012医疗服务基本数据集》共有3个分册，分别是第1部分：门诊摘要，第2部分：住院摘要，第3部分：成人健康体检。其中门诊摘要不包括：（）
    A

    门诊号

    B

    单位类别代码

    C

    咨询问题

    D

    卫生服务要求

    E

    处置计划


    正确答案： C
    解析： 暂无解析

  • 第10题：

    单选题
    若某个次数分布表中，从最低组往最高组的方向累加，结果“60~65”组的累积次数是30，“65~70”组的累积次数是48，那么下列表述正确的是（）
    A

    60分以下的有30人

    B

    65分以上的有30人

    C

    69.5分以下的有48人

    D

    69.5分以上的有48人


    正确答案： A
    解析： 暂无解析

  • 第11题：

    单选题
    在标志寄存器中，CY=0，Z=0，S=0分别表示（）。
    A

    无进位，运算结果为0，运算结果为负

    B

    无进位，运算结果非0，运算结果为正

    C

    有进位，运算结果非0，运算结果为正

    D

    有进位，运算结果为0，运算结果为负


    正确答案： C
    解析： 暂无解析

  • 第12题：

    问答题
    （2分钟，结束前10秒时，有提示音）一次长跑比赛，一个选手以一步之差落在了后面，成为第4名。他受到的责难远比那些成绩更差的选手多。大家都说：“真是白跑了，这跟倒数第一有什么区别？”但是这个选手说：“虽然没有得奖，但是在所有没得到名次的选手中，我名列第一！”

    正确答案：
    Yícì chángpǎo bǐsài,yígè xuǎnshǒu yǐ yíbùzhīchā luò zài lè hòumiàn,chéngwéi dìsì míng.Tā shòudào de zénàn yuǎn bǐ nàxiē chéngjì gèng chà de xuǎnshǒu duō.Dàjiā dōu shuō:“Zhēn shì bái pǎo le,zhè gēn dàoshǔ dìyī yǒu shénme qūbié?”Dànshì zhège xuǎnshǒu shuō:“Suīrán méiyǒu déjiǎng,dànshì zài suǒyǒu méi dédào míngcì de xuánshǒu zhōng,wǒ mínglièdìyī!”
    解析： 暂无解析

  • 第13题：

    有三名国际象棋特级大师和三名国际象棋大师进行一场循环比赛，即每一名选手都要和其他五名选手比赛。比赛计分规则如下：击败国际象棋特级大师可得2分，击败国际象棋大师可得1分；国际象棋特级大师输一场失2分，国际象棋大师输一场失1分。

    如果现有一名国际象棋特级大师已输了两场，那么他最高可获几分?（ ）

    A．0分

    B．1分

    C．2分

    D．3分


    正确答案：B
    B
    在输两场的情况下，要想获得最高分只能是剩余三场全赢，三场中两位是国际象棋特级大师，一位是国际象棋大师，这样也只能得到1分。

  • 第14题：

    在环保知识竞赛中，男选手的平均得分为80分，女选手的平均得分为65分，全部选手的平均得分为72分。已知全部选手人数在35到50之间，则全部选手人数为：

    A48
    B45
    C43
    D40


    答案：B
    解析：
    题干为平均分计算问题，可利用十字交叉思想快速求解。根据十字交叉法，可列式为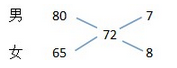：可以得出，男女选手人数之比为，则男女选手总人数应为15的倍数，查看选项，只有B项符合。

    故正确答案为B。

  • 第15题：

    五位选手在一次物理竞赛中共得412分,每人得分互不相等且均为整数,其中得分最高的选手得90分,那么得分最少的选手至多得（ ）分

    A.77
    B.78
    C.79
    D.80
    E.81

    答案：C
    解析：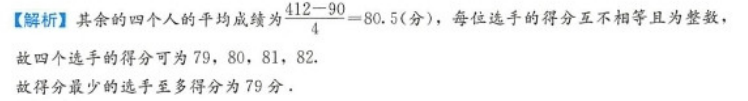

  • 第16题：

    一次国际象棋比赛，有10名选手参加，每名选手都要与其他选手比赛一次，选手们的得分全不一样。已知：
    (1)第一名选手和第二名选手一次都没有输；
    (2)前两名的总分比第三名选手多10分；
    (3)第四名选手与最后四名选手的得分和相等。
    (每局棋胜者得1分，负者得0分，平局每人得0. 5分）
    请问:从第一名到第六名共得分数为（）。
    A. 46 B. 25 C. 18 D. 39


    答案：D
    解析：
    单循环赛，每人赛9盘棋，所以最高分为9分，前两名都没有输，说明没有全胜的人。所以，最高分最多为8. 5分。
    那么，第二名最多8分，第三名最多8.5+8-10 = 6. 5（分），第四名最多6分。
    后四名选手之间要赛4X3 /2=6（盘）。
    每盘出现1分，这四人之间要累计6分，那么这四人的总分至少要有6分，就是说第四名的分数至少是6分。
    综合“第四名最多6分”“第四名的分数至少是6分”，可知第四名的得分应该是6分。
    由此可知：第三名6. 5分，第四名6分，第一名是8. 5分，第二名是8分，后四人最后总分是6分。
    10名选手的循环赛总盘数是1/2x10x(10-1)=45(盘)，总分是1x45 = 45(分)。故第一到第六名共得的分数为45-6=39(分)。所以本题选D。

  • 第17题：

    柏拉图说：“法律有一部分是为有美德的人制定的，如果他们愿意和平善良地生活，那么法律可以教会他们在与他人的交往中所要遵循的准则;法律也有一部分是为那些不接受教诲的人制定的，这些人顽固不化，没有任何办法能使他们摆脱罪恶。”这段话所凸显的法律的规范作用是（　）。

    • A、教育作用 
    • B、保障作用 
    • C、预测作用 
    • D、强制作用

    正确答案:A,D

  • 第18题：

    若某个次数分布表中，从最低组往最高组的方向累加，结果“60~65”组的累积次数是30，“65~70”组的累积次数是48，那么下列表述正确的是（）

    • A、60分以下的有30人
    • B、65分以上的有30人
    • C、69.5分以下的有48人
    • D、69.5分以上的有48人

    正确答案:C

  • 第19题：

    对于不合规则的器械，个人选手扣0.3分，集体选手扣0.5分。


    正确答案:错误

  • 第20题：

    在环保知识竞赛中，男选手的平均得分为80分，女选手的平均得分为65分，全部选手的平均得分为72分。已知全部选手人数在35到50之间，则全部选手人数为（）。

    • A、48
    • B、45
    • C、43
    • D、40

    正确答案:B

  • 第21题：

    问答题
    有一场体育比赛中，共有N个项目，有运动员1号，2号，3号参加。在每一个比赛项目中，第一，第二，第三名分别得A，B，C分，其中A，B，C为正整数，且A>B>C。最后1号选手共得22分，2号与3号均得9分，并且2号在百米赛中取得第一。最后，求N的值，并分析出谁在跳高中得第二名。

    正确答案： 因为1号、2号、3号三人共得分为22+9+9=40分，又因为三名得分均为正整数且不等，所以前三名得分最少为6分。40=5*8=4*10=2*20=1*20，不难得出项目数只能是5。即N=5。1号总共得22分，共5项，所以每项第一名得分只能是5，22=5*4+2，故1应得4个一名1个二名.第二名得1分，又因为2号百米得第一，所以1只能得这个第二。2号共得9分，其中百米第一5分，其它4项全是1分，9=5+1=1+1+1。即2号除百米第一外全是第三，跳高第二必定是3号所得。
    解析： 暂无解析

  • 第22题：

    单选题
    进行两个补码整数9CH和7AH相加运算后，会产生（）。
    A

    无溢出且无进位

    B

    无溢出但有进位

    C

    有溢出且有进位

    D

    有溢出但无进位


    正确答案： D
    解析： 暂无解析

  • 第23题：

    单选题
    在标志寄存器下中，Z=1，CY=1分别表示（）。
    A

    计算结果不为0，无进位

    B

    计算结果为0，有进位

    C

    计算结果为0，无进位

    D

    计算结果不为0，有进位


    正确答案： B
    解析： 暂无解析

相关内容