itgle.com

一家市场调查公司想估计某地区有彩色电视机的家庭所占的比例。该公司希望对总体比例的估计误差不超过0．05，要求的可靠程度为95%，应取多大容量的样本(没有可利用的总体比例估计值)。

题目
一家市场调查公司想估计某地区有彩色电视机的家庭所占的比例。该公司希望对总体比例的估计误差不超过0．05，要求的可靠程度为95%，应取多大容量的样本(没有可利用的总体比例估计值)。

相似考题

1.常用的点估计是用样本均值估计总体均值，用样本比例估计总体比例，用样本方差估计总体方差。（ ）此题为判断题(对，错)。

2.一个从事市场研究的公司想知道某市内至少有一个成员看过某种报纸广告的家庭占多大比例。为了估计这个比例,首先要确定抽多少个家庭做调查。该公司希望以 90% 的置信水平对这个比例作出估计,并使估计值处在真正比例附近 0.04 范围之内。在一个由 15 个家庭组成的预备样本中,有 35% 的响应者指出他们家中有某个人看过这种广告,试问应取多大的样本。

3.某地欲调查7岁以上儿童参加过夏令营的比例,在预调查中这个比例为85%,要求正式调查时所得的样本率与未知总体率相差不超过5%的可能性不大于0.05,请问这是什么设计方案?()A、总体率估计B、两组配对设计率比较C、两独立样本率比较D、多组样本率比较E、以上都不是

4.一项研究中要对贫困户的比例进行推断。在95％的置信度下要求误差不超过±3％。采用重置简单随机抽样中，已知z0．025=1．96，则以下说法正确的有( )。A.如果总体中贫困户的比例估计为30％，则必要样本容量为896人B.如果总体中贫困户的比例估计为30％，则必要样本容量为897人C.如果缺乏关于总体中贫困户比例的信息，则必要样本容量为1068人D.如果缺乏关于总体中贫困户比例的信息，则必要样本容量为1067人E.如果缺乏关于总体中贫困户比例的信息，则必要样本容量无法计算

参考答案和解析
答案：
解析：
解：已知E=0．05，a=0．05，za/2=z0.025=1．96 由于总体比例的估计值未知，我们可以采用7r=0．5，计算必要的样本容量：



为了以95%的可靠程度保证估计误差不超过0．05，应取385户进行调查。
更多“一家市场调查公司想估计某地区有彩色电视机的家庭所占的比例。该公司希望对总体比例的估计误差不超过0．05，要求的可靠程度为95%，应取多大容量的样本(没有可利用的总体比例估计值)。”相关问题

  • 第1题：

    总体比例的估计,是具有某特征的单元总数的估计值除以总体中单元总数的估计值。()

    此题为判断题(对，错)。


    答案：对

    解析：总体比例的估计，是指总体中具有某一相同标志表现的单位数占全部总体单位数的比重，所以题干正确。

  • 第2题：

    在确定总体比例估计中的样本容量时，如果缺少比例的方差，常取比例值为0．5。

    此题为判断题(对，错)。


    正确答案：√

  • 第3题：

    在估计总体比例时样本量的确定中，由于总体比例的值是固定的，因而估计误差主要由样本量来确定。

    此题为判断题(对，错)。


    正确答案：√

  • 第4题：

    常用的点估计是用样本均值估计总体均值，用样本比例估计总体比例，用样本方差估计总体方差。（ ）


    答案：对
    解析：

  • 第5题：

    样本比例是总体比例的无偏估计量。（ ）


    答案：对
    解析：

  • 第6题：

    汽车经销商为开发市场欲估计某地区拥有汽车的家庭所占的比例。此项调查要求估计误差不超过0．05，可靠程序为95%，则样本容量（ ）。(注：没有可利用的总体比例百值)[2012年初级真题]



    答案：B,C,E
    解析：
    设E代表允许的估计误差，可以得到估计总体比例时所需的样本量，计算公式为：



    式中，估计误差E由使用者预先确定。大多数情况下。E的取值一般应小于0．1。如果总体比例π的值不知道可以用样本比例P来代替，或者取π=0．5，使得π(1-π)达到最大。

  • 第7题：

    在确定总体比例估计中的样本容量时，如果缺少比例的方差，常取比例值为0．5。
    A.√


    答案：对
    解析：

  • 第8题：

    决定样本量大小的因素有（）

    • A、置信水平
    • B、总体方差
    • C、允许的估计误差
    • D、总体均值
    • E、总体比例

    正确答案:A,B,C

  • 第9题：

    区间估计的要素是（）

    • A、点估计值
    • B、样本的分布
    • C、估计的可靠度
    • D、抽样极限误差
    • E、总体的分布形式

    正确答案:A,C,D

  • 第10题：

    多选题
    一项研究中要对贫困户的比例进行推断。在95%的置信度下要求误差不超过±3%。采用重置简单随机抽样中，已知z0.025=1．96，则以下说法正确的有（）。
    A

    如果总体中贫困户的比例估计为30%，则必要样本容量为896人

    B

    如果总体中贫困户的比例估计为30%，则必要样本容量为897人

    C

    如果缺乏关于总体中贫困户比例的信息，则必要样本容量为1068人

    D

    如果缺乏关于总体中贫困户比例的信息，则必要样本容量为1067人

    E

    如果缺乏关于总体中贫困户比例的信息，则必要样本容量无法计算


    正确答案： E,A
    解析： 暂无解析

  • 第11题：

    单选题
    为了估计总体比例π，已经求得其95%的置信区间为（82%，88%），下列说法中错误的是（　　）。[2014年初级真题]
    A

    点估计值为85%

    B

    此次估计的误差范围是3%

    C

    用该方法估计的可靠程度95%

    D

    总体比例落在这个置信区间的概率为95%


    正确答案： B
    解析：
    该置信区间由样本统计量加减估计误差得到，关于点估计值对称，因此点估计值为（82%＋88%）÷2＝85%，估计的误差范围为3%，估计的可靠程度为95%。总体比例是一个固定的未知数，要么落在这个置信区间内，要么在这个置信区间外，即落在这个置信区间的概率为0或1，不能说“落在这个置信区间的概率为95%”。

  • 第12题：

    多选题
    常用的点估计有（  ）。
    A

    用样本均值估计总体均值

    B

    用样本比例估计总体比例

    C

    用样本方差估计总体方差

    D

    用总体均值估计样本均值

    E

    有总体方差估计样本方差


    正确答案： D,E
    解析：

  • 第13题：

    一家广告公司想估计某类商店去年所花的平均广告费有多少。经验表明，总体方差约为1800000。如置信度取95%，并要使估计值处在总体平均值附近500元的范围内，这家广告公司应取多大的样本?


    正确答案：
    已知σ2=1800000，α=0．05，zα/2=1．96，E=500

    这家广告公司应抽选28个商店作样本。 

  • 第14题：

    一家市场调查公司想估计某地区有彩色电视机的家庭所占的比例。该公司希望对总体比例的估计误差不超过0．05，要求的可靠程度为95%，应取多大容量的样本?(没有可利用的总体比例估计值)。


    正确答案：
    已知E=0．05，α=0．05，zα/2=z0．025=1．96
    由于总体比例的估计值未知，我们可以采用π=0．5，计算必要的样本容量： 

    为了以95%的可靠程度保证估计误差不超过0．05，应取385户进行调查。 

  • 第15题：

    为了估计总体比例π，已经求得其95%的置信区间为（82%，88%），下列说法中错误的是（ ）。

    A.点估计值为85%

    B.此次估计的误差范围是±3%

    C.用该方法估计的可靠程度95%

    D.总体比例落在这个置信区间的概率为95%


    正确答案：D

  • 第16题：

    常用的点估计有（ ）。

    A.用样本均值估计总体均值
    B.用样本比例估计总体比例
    C.用样本方差估计总体方差
    D.用总体均值估计样本均值
    E.有总体方差估计样本方差

    答案：A,B,C
    解析：

  • 第17题：

    在估计总体比例时所需样本量的计算公式为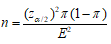

    当总体比例π未知时，就无法根据上述公式确定样本容量。


    答案：错
    解析：

  • 第18题：

    汽车经销商为开发市场欲估计某地区拥有汽车的家庭所占的比例。此项调查要求估计误差不超过0.05,可靠程度为95%,则样本容量()(注:没有可利用的总体比例π值)

    A.无法确定
    B.计算公式中的π可以采用试验性调查估计的样本比例来代替
    C.计算公式中的π可以取0.5
    D.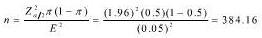,即取384户调查
    E.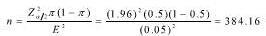,即取385户调查

    答案：B,C,E
    解析：

  • 第19题：

    常用的点估计有（）

    • A、用样本均值估计总体均值
    • B、用样本比例估计总体比例
    • C、用样本方差估计总体方差
    • D、用总体均值估计样本均值
    • E、有总体方差估计样本方差

    正确答案:A,B,C

  • 第20题：

    下列样本说法中正确的有（）。

    • A、样本均值是总体均值的无偏估计量
    • B、样本比例是总体比例的无偏估计量
    • C、样本均值是总体均值的一致估计量
    • D、样本标准差是总体标准差的无偏估计量
    • E、样本方差是总体方差的无偏估计量

    正确答案:A,B,C,E

  • 第21题：

    为了利用样本比例估计总体比例而进行抽样，现需确定必要样本量。但没有可依据的历史数据或类似空间的数据，设定的比例应为（）。

    • A、0.05
    • B、0.25
    • C、0.5
    • D、0.15

    正确答案:A

  • 第22题：

    判断题
    样本比例是总体比例的无偏估计量。（　　）
    A

    对

    B

    错


    正确答案： 错
    解析：
    E（p）=π，所以样本比例是总体比例的无偏估计量。

  • 第23题：

    判断题
    常用的点估计是用样本均值估计总体均值，用样本比例估计总体比例，用样本方差估计总体方差。（　　）
    A

    对

    B

    错


    正确答案： 对
    解析：
    点估计是用样本统计量的实现值来近似相应的总体参数。总体均值、总体比例、总体方差是三个通常需要被了解的值，因为样本均值、样本比例和样本方差分别是总体均值、总体比例和总体方差的无偏估计，因此由样本值去估计相应的总体值。

  • 第24题：

    多选题
    A

    如果总体中贫困户的比例估计为30%，则必要样本容量为896人

    B

    如果总体中贫困户的比例估计为30%，则必要样本容量为897人

    C

    如果缺乏关于总体中贫困户比例的信息，则必要样本容量为1068人

    D

    如果缺乏关于总体中贫困户比例的信息，则必要样本容量为1067人

    E

    如果缺乏关于总体中贫困户比例的信息，则必要样本容量无法计算


    正确答案： D,C
    解析：

相关内容