itgle.com

一个舞会中，一群人戴帽子。黑的帽子或白的帽子，至少有一人戴黑帽子。自己不能看到自己戴的帽子颜色，可以看到别人的。如果知道自己戴黑帽子就打自己的耳光。第一次熄灯，没有任何声音。亮灯，再熄灯。第2次还是没有声音。亮灯，再熄灯。第3次，一片“拍拍拍”的响声。问有几个人戴黑帽子？

题目

一个舞会中，一群人戴帽子。黑的帽子或白的帽子，至少有一人戴黑帽子。自己不能看到自己戴的帽子颜色，可以看到别人的。如果知道自己戴黑帽子就打自己的耳光。第一次熄灯，没有任何声音。亮灯，再熄灯。第2次还是没有声音。亮灯，再熄灯。第3次，一片“拍拍拍”的响声。问有几个人戴黑帽子？

相似考题

1.关于穿减及脱摘防护物品的流程,以下哪项是正确的()。A、穿戴防护物品流程;洗手或手消毒→戴医用防护口罩→戴帽子→穿工作服→穿隔离衣→戴手套B、穿戴防护物品流程:洗手或手消毒→穿工作服→戴医用防护口罩→戴帽子→穿隔离衣→戴手套C、穿戴防护物品流程:洗手或手消毒→穿工作服→戴医用防护口罩→戴帽子→戴手套→穿隔离衣D、穿戴防护物品流程:洗手或手消毒→戴帽子→戴医用防护口罩→穿工作服→穿隔离衣→戴手套E、脱调防护物品流程:戴手套→洗手或手消毒→脱隔离衣→洗手或手消毒→摘口罩帽子

2.一群人开舞会，每人头上都戴着一顶帽子。帽子只有黑白两种，黑的至少有一顶。每个人都能看到其他人帽子的颜色，却看不到自己的。主持人先让大家看看别人头上戴的是什么帽子，然后关灯，如果有人认为自己戴的是黑帽子，就打自己一个耳光。第一次关灯，没有声音。于是再开灯，大家再看一遍，关灯时仍然鸦雀无声。一直到第三次关灯，才有劈劈啪啪打耳光的声音响起。问有多少人戴着黑帽子？

3.逻辑二:甲 乙丙三方各带一顶帽子丙个是瞎子 帽子有黑白两种颜色 并不是所有的都是白色他们只能看到另外两个人的帽子颜色不能看到自己的帽子颜色甲睁开眼看了看 说不能确定自己的帽子颜色乙睁开眼睛 也说不能确定自己的帽子颜色丙说：“我知道自己的帽子颜色了”请问 丙的帽子是什么颜色 为什么？

4.下面关于穿防护服的流程,描述正确的是()。A、洗手→戴帽子、口罩→穿防护服→穿隔离衣→戴护目镜→穿靴套、鞋套B、洗手→穿防护服→戴帽子、口罩→穿隔离衣→戴护目镜→穿靴套、鞋套C、洗手→戴护目镜→穿防护服→戴帽子、口罩→穿隔离衣→穿靴套、鞋套D、洗手→穿防护服→戴护目镜→戴帽子、口罩→穿隔离衣→穿靴套、鞋套R、洗手→穿防护服→戴帽子、 口罩→戴护目镜→穿隔离衣→穿靴套、鞋套

更多“一个舞会中,一群人戴帽子。黑的帽子或白的帽子,至少有一人戴黑帽子。自己不能看到自己戴的帽子颜 ”相关问题

  • 第1题：

    甲、乙、丙三个学生分别戴着三种不同颜色的帽子，穿着三种不同颜色的衣服去参加大运会志愿者服务活动。已知：（1）帽子和衣服的颜色都只有红、黄、白三种；（2）甲没戴红帽子，乙没戴黄帽子；（3）戴红帽子的学生没有穿白衣服；（4）戴黄帽子的学生穿着红衣服；（5）乙没有穿黄衣服。试问：对三人所戴帽子和所穿衣服判断正确的是（ ）。

    A.甲戴白色帽子，乙穿红色衣服
    B.甲戴黄色帽子，穿白色衣服
    C.乙穿白色衣服，丙戴红色帽子
    D.甲穿红色衣服，丙穿白色衣服

    答案：C
    解析：
    根据（2）知道乙没有戴黄色的帽子。
    首先设乙帽子为红色。由于（3）戴红帽子的学生没有穿白衣服，则乙没有穿白衣服。由于（5）乙没有穿黄衣服，则乙衣服为红色。但是与（4）戴黄帽子的学生穿着红衣服相矛盾，故乙帽子为红色是不可能的。
    因此乙的帽子只能为白色。由于（2）甲没戴红帽子，则甲戴黄帽子，于是丙戴红帽子。根据（4）戴黄帽子的学生穿着红衣服，则甲穿红衣服。而（5）乙没有穿黄衣服，则乙穿白衣服，丙穿黄衣服。具体参见下表说明：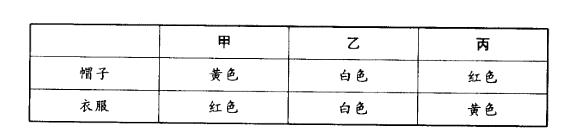

  • 第2题：

    甲、乙、丙三个学生分别戴着三种不同颜色的帽子,穿着三种不同颜色的衣服去参加一次争办奥运的活动。已知：（1）帽子和衣服的颜色都只有红、黄、蓝三种;（2）甲没戴红帽子,乙没戴黄帽子;（3）戴红帽子的学生没有穿蓝衣服;（4）戴黄帽子的学生穿着红衣服;（5）乙没有穿黄色衣服。试问:甲、乙、丙三人各什么颜色的帽子,穿什么颜色的衣服?

    A.甲戴蓝帽子穿红衣服。
    B.乙戴蓝帽子穿蓝衣服。
    C.丙戴黄帽子穿黄衣服。
    D.甲戴蓝帽子穿蓝衣服。
    E.丙戴红帽子穿红衣服。

    答案：B
    解析：
    第一步:明确维度和组度。3个维度:学生、帽子颜色和衣服颜色。3个组度:甲、乙、丙三人。第二步:画出对应表格,并将题干信息转移到表格中。



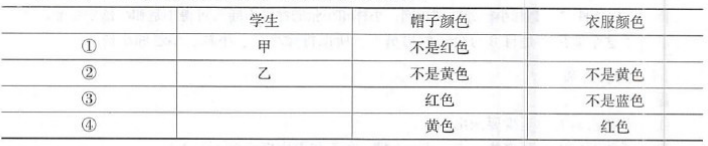
    第三步:观察“重复出现”的内容作为突破口:（1）②④中帽子颜色都出现了“黄色”这一信息,可得乙不穿红衣服;又已知乙不穿黄衣服,所以乙只能穿蓝衣服。（2）由上一步可知②中“衣服颜色”一列为“蓝色”,此时②③中衣服颜色都出现了“蓝色”这一信息,可得:乙不戴红帽子,又已知乙不戴黄帽子,所以乙只能戴蓝帽子。（3）甲不戴红帽子,不戴乙的蓝帽子,只能戴黄帽子,再由④知穿红衣服。（4）剩下的丙则为戴红帽子穿黄衣服。

  • 第3题：

    有甲、乙、丙、丁、戊五个人，每个人头上戴一顶白帽子或者黑帽子，每个人显然只能看见别人头上帽子的颜色，看不见自己头上帽子的颜色。并且，一个人戴白帽子当且仅当他说真话，戴黑帽子当且仅当他说假话。已知：
    甲说：我看见三顶白帽子一顶黑帽子。
    乙说：我看见四顶黑帽子。
    丙说：我看见一顶白帽子三顶黑帽子。
    戊说：我看见四顶白帽子。
    根据上述题干，下列陈述都是假的，除了（ ）

    A.甲和丙都戴白帽子
    B.乙和丙都戴黑帽子
    C.戊戴白帽子，但丁戴黑帽子
    D.丙戴黑帽子，但甲戴白帽子
    E.丙和丁都戴白帽子

    答案：E
    解析：
    解这道题只能用假设法和归谬法。先假设甲的话为真，则甲戴白帽子，加起来共有四顶白帽子一顶黑帽子，于是乙和丙的话就是假的，于是乙和丙都戴黑帽子，这与A项的话为真的结果（一顶黑帽子）矛盾，因此A项的话不可能为真，必定为假。再假设乙的话为真，则他自己戴白帽子，共有一顶白帽子四顶黑帽子；这样，由于丙看不见他自己所戴帽子的颜色，当他说“我看见一顶白帽子三顶黑帽子”时，他所说的就是真话，于是他戴白帽子，这样乙和丙都戴白帽子，有两顶白帽子，与乙原来的话矛盾。所以，乙所说的只能是假话，他戴黑帽子。既然已经确定甲、乙都戴黑帽子，则戊所说的“我看见四顶白帽子”就是假话，戊也戴黑帽子。现假设丙的话为假，则他实际看见的都是黑帽子，他自己也戴黑帽子，于是五个人都戴黑帽子，这样，乙的话就是真话；但我们已经证明乙的话不可能为真，因此丙的话也不可能为假，于是丙和未说话的丁戴白帽子。最后结果是：甲、乙、戌说假话，戴黑帽子；丙、丁说真话，戴白帽子。所以，正确的选项是E项。##niutk

  • 第4题：

    一群人开舞会,每人头上都戴着一顶帽子。帽子只有黑白两种,黑的至少有一顶。每个人都能看到其他人帽子的颜色,却看不到自己的。主持人先让大家看看别人头上戴的是什么帽子,然后关灯,如果有人认为自己戴的是黑帽子,就拍自已的手。第一次关灯,没有声音。于是再开灯,大家再看一遍,关灯时仍然鸦雀无声。一直到第三次关灯,才有噼噼啪啪拍手的声音响起。问有多少人戴着黑帽子?

    A.一人。
    B.两人。
    C.三人。
    D.四人。
    E.无法判断。

    答案：C
    解析：
    第一步:明确情景设置。①至少一黑;②每个人都能看到其他人帽子的颜色,却看不到自己的。第二步:分析每一轮情况。

  • 第5题：

    有甲、乙、丙、丁、戊五个人，每个人头上戴一顶内帽子或者黑帽子，每个人显然只能看见别人头上帽子的颜色，看不见自己头上帽子的颜色。并且，一个人戴白帽子当且仅当他说真话，戴黑帽子当且仅当他说假话。已知：
    甲说：我看见三顶白帽子一顶黑帽子。
    乙说：我看见四顶黑帽子。
    丙说：我看见一顶白帽子三顶黑帽子。
    戊说：我看见四顶白帽子。
    根据上述题干，下列陈述都是假的，除了（ ）

    A、甲和丙都戴白帽子
    B、乙和丙都戴黑帽子

    C、戊戴白帽子，但丁戴黑帽子
    D、丙戴黑帽子，但甲戴白帽子

    E、丙和丁都戴白帽子


    答案：E
    解析：
    解这道题只能用假设法和归谬法。先假设甲的话为真，则甲戴白帽子，加起来共有四顶白帽子一顶黑帽子，于是乙和丙的话就是假的，于是乙和丙都戴黑帽子，这与A项的话为真的结果（一顶黑帽子）矛盾，因此A项的话不可能为真，必定为假。再假设乙的话为真，则他自己戴白帽子，共有一顶白帽子四顶黑帽子；这样，由于丙看不见他自己所戴帽子的颜色，当他说“我看见一顶白帽子三顶黑帽子”时，他所说的就是真话，于是他戴白帽子，这样乙和丙都戴白帽子，有两顶白帽子，与乙原来的话矛盾。所以，乙所说的只能是假话，他戴黑帽子。既然已经确定甲、乙都戴黑帽子，则戊所说的“我看见四顶白帽子”就是假话，戊也戴黑帽子。现假设丙的话为假，则他实际看见的都是黑帽子，他自己也戴黑帽子，于是五个人都戴黑帽子，这样，乙的话就是真话；但我们已经证明乙的话不可能为真，因此丙的话也不可能为假，于是丙和未说话的丁戴白帽子。最后结果是：甲、乙、戌说假话，戴黑帽子；丙、丁说真话，戴白帽子。所以，正确的选项是E项。

相关内容