itgle.com

1. 设直线L的方程为则L的参数方程是（　　）。

题目
1. 设直线L的方程为

则L的参数方程是（　　）。

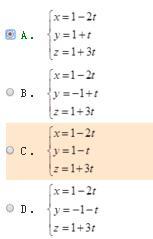
相似考题

1.已知曲线C为y= 2x2，直线l为y= 4x．（10分）(1)求由曲线C与直线l所围成的平面图形的面积S；(2)求过曲线C且平行于直线l的切线方程．

2.设平面方程为x+y+z+1=0，直线方程为1－x=y+1=z，则直线与平面： A.平行 B.垂直 C.重合 D.相交但不垂直

3.设曲线y=y(x)上点P(0，4)处的切线垂直于直线x-2y+5=0，且该点满足微分方程y″+2y′+y=0，则此曲线方程为( )。A. B. C. D.

4.假定被研究现象基本上是按不变的发展速度发展,为描述现象变动的趋势,借以进行预测,应拟合的方程为( )。A. 直线趋势方程B. 指数曲线方程C. 双曲线方程D. 直线或曲线方程均可

更多“1. 设直线L的方程为 ”相关问题

  • 第1题：

    设方程y´´-4y´+3y=0的某一积分曲线，它在点(0，2)处与直线x-y+2=0相切，则该积分曲线的方程是( ).

    A.
    B.
    C.
    D.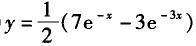

    答案：B
    解析：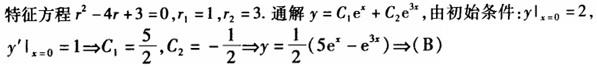

  • 第2题：

    设L为连接(0，2)和(1，0)的直线段，


    答案：D
    解析：
    提示:利用已知两点求出直线方程L:y=-2x+2，

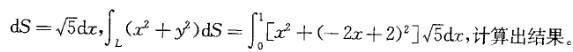
  • 第3题：

    过点M(3，-2，1)且与直线L :平行的直线方程是：


    答案：D
    解析：
    直线L是平面χ - y- z +1 = 0和平面2χ+ y - 3z + 4 = 0的交线，直线L的方向向量

  • 第4题：

    已知曲线C为y=2x2及直线L为y=4x．
    ①求由曲线C与直线L所围成的平面图形的面积S；
    ②求曲线C的平行于直线L的切线方程．


    答案：
    解析：
    画出平面图形如图l一3—4阴影所示．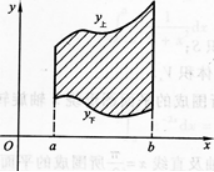
    图1—3—3

    图1—3—4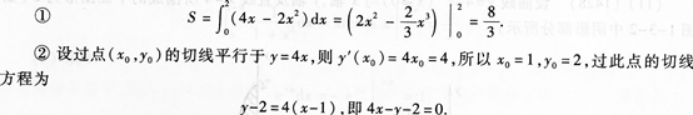

  • 第5题：

    设η为非零向量,A=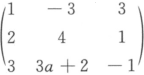,η为方程组AX=O的解,则a=_______,方程组的通解为_______.


    答案：1、3 2、k(-3 3、1 4、2)^T
    解析：

  • 第6题：

    设曲线L的方程为 ， （I）求L的弧长； （II）设D是由曲线L，直线x=1，x=e及x轴所围平面图形，求D的形心的横坐标


    答案：
    解析：

  • 第7题：

    点M（-5,1）关于y轴的对称点M'与点N（1,一1）关于直线l对称,则直线l的方程是（ ）



    答案：C
    解析：

  • 第8题：

    高中数学《直线的两点方程式》
    一、考题回顾



    二、考题解析
    【教学过程】
    (一)导入新课
    利用点斜式方程求解直线方程：




    【答辩题目解析】
    1.两点式方程是根据什么推导出来的?为什么要推导两点式?
    2.本节课的教学目标是什么?


    答案：
    解析：
    1、两点式方程是根据点斜式方程推导而来。题目来源于考生回忆
    两点式相对于点斜式方程而言，如果知道直线上的两点，很容易写出直线方程，另外两点式更具有对称，形式更美观、更整齐，便于记忆。

    2、【知识与技能】掌握直线方程的两点的形式特点及适用范围，能根据两点求直线的点斜式方程。题目来源于考生回忆
    【过程与方法】通过应用直线的点斜式方程的探究过程中获得两点式方程，增强比较、分析、应用的能力。
    【情感态度与价值观】通过学习直线的两点式方程的特征和适用范围，渗透数学中普遍存在相互联系、相互转化等观点。

  • 第9题：

    设直线的方程为x=y-1=z， 平面的方程为x-2y+z=0，则直线与平面（ ）。
    A.重合 B.平行不重合 C.垂直相交 D.相交不垂直


    答案：B
    解析：
    正确答案为B。
    提示：直线的方向向量为s = (1，1，1)，平面的法向量为n= (1，-2，1)，s·n = 1-2 + 1 = 0,这两个向量垂直，直线与平面平行，又直线上的点(0，1，0)不在平面上，故直线与平面不重合。

  • 第10题：

    在同一平面内，直线与圆弧相切，计算切点坐标的方法是（）。

    • A、将直线方程与圆方程联立求公共解
    • B、将直线方程代入圆方程求解
    • C、将圆方程代入直线方程求解
    • D、将两个方程相加消元求解

    正确答案:A

  • 第11题：

    设直线的方程为x=y-1=z，平面的方程为x-2y+z=0，则直线与平面（）。

    • A、重合
    • B、平行不重合
    • C、垂直相交
    • D、相交不垂直

    正确答案:B

  • 第12题：

    单选题
    设直线的方程为x=y-1=z，平面的方程为x-2y+z=0,则直线与平面（ ）
    A

    重合

    B

    平行不重合

    C

    垂直相交

    D

    相交不垂直


    正确答案： C
    解析：

  • 第13题：

    设平面方程x+y+Z+1=0，直线的方程是l-x=y+1= z，则直线与平面：
    (A)平行 （B)垂直 (C)重合 (L)相交但不垂直


    答案：D
    解析：
    解：选D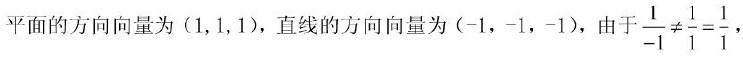
    所以直线与平面不垂直。又1x(-1) + 1x1+1x1=1≠0，所以直线与平面不平行。

  • 第14题：

    设直线方程为x=y-1=z，平面方程为x-2y+z=0，则直线与平面：
    A.重合 B.平行不重合
    C.垂直相交 D.相交不垂直


    答案：B
    解析：
    从而知直线//平面或直线与平面重合；再在直线上取一点（0,1,0），验证该点是否满足平面方程。

  • 第15题：

    设平面方程:x + y + z-1 = 0，直线的方程是1-x = y + 1=z，则直线与平面：
    A.平行 B.垂直 C.重合 D.相交但不垂直


    答案：D
    解析：

  • 第16题：



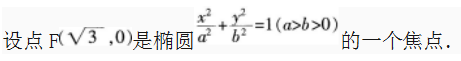
    且与椭圆短轴的两个端点组成等边三角形。
    (1)求椭圆的方程；
    (2)过点F作一直线l交椭圆于A，B两点，设F1为椭圆的另一个焦点，当 △F1AB的面积最大时，求l的方程。


    答案：
    解析：



  • 第17题：

    设封闭曲线L的极坐标方程为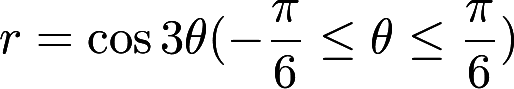，则L所围成的平面图形的面积为


    答案：
    解析：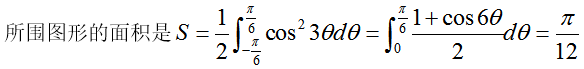

  • 第18题：

    设直线L过A(1，0，0)，B(0，1，1)两点，将L绕z轴旋转一周得到曲面∑，∑与平面z=0，z=2所围成的立体为Ω.
    　　(Ⅰ)求曲面∑的方程；
    　　(Ⅱ)求Ω的形心坐标.


    答案：
    解析：
    【分析】利用定义求旋转曲面∑的方程；利用三重积分求Ω的形心坐标.

  • 第19题：

    设圆C与圆（x-5）2+y2=2关于直线y=2x对称，则圆C的方程为



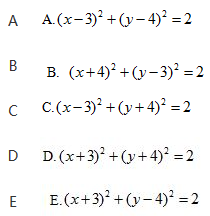    答案：E
    解析：

  • 第20题：

    在平面直角坐标系中，以坐标原点0为极点，x轴的正半轴为极轴建立极坐标系。已知 点A的极坐标为．直线Z的极坐标方程为且点A在直线Z上。
    (1)求。的值及直线Z的直角坐标方程；
    (2)圆C的参数方程为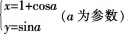试判断直线Z与圆C的位置关系。


    答案：
    解析：
    所以直线l与圆C相交。

  • 第21题：

    已知中心在坐标原点0的椭圆C经过点A(2，3)且点F(2，0)为其右焦点。
    (1)求椭圆C的方程；
    (2)是否存在平行于OA的直线l，使l与椭圆C有公共点，且直线OA与l的距离等于4，若存在，求l方程；若不存在，请证明。


    答案：
    解析：

  • 第22题：

    根据下列资料编制直线回归方程r=0.9a=2.8（）

    • A、直线回归方程yc=2.8+1.08x
    • B、直线回归方程yc=2.8+1.18x
    • C、直线回归方程yc=0.9+1.08x
    • D、直线回归方程yc=0.9+1.18x

    正确答案:A

  • 第23题：

    单选题
    设直线方程为x=y-1=z，平面方程为x-2y+z=0，则直线与平面（　　）。[2011年真题]
    A

    重合

    B

    平行不重合

    C

    垂直相交

    D

    相交不垂直


    正确答案： C
    解析：
    直线的方向向量s＝（1，1，1），平面的法向向量n＝（1，－2，1），其向量积s·n＝1－2＋1＝0，则这两个向量垂直，即直线与平面平行。又该直线上的点（0，1，0）不在平面上，故直线与平面不重合。

相关内容