设f(x)=sin2t+cost+arctant，则f1(t)=( )。

题目

相似考题

1.设有以下说明:type t1=file of integer; var f1:t1;n:integer; 且abc.dat是t1型文件,下面正确的程序段是Aassign(f1,‘abc.dat‘); write(f1,n); rewrite(f1); close(f1);Bassign(f1,‘abc.dat‘); reset(f1); readln(f1,n); close(f1);Cassign(f1,‘abc.dat‘); rewrite(f1); writeln(f1,n); close(f1);Dassign(f1,‘abc,dat‘); rewrite(f1); read(f1,n); close(f1);

2.设R、N分别表示实数、整数和自然数集,下面定义函数f1、f2、f3:f1:R→R,f(x)=2xf2:N→N×N,f(n)=f设R、N分别表示实数、整数和自然数集，下面定义函数f1、f2、f3： f1：R→R，f(x)=2x f2：N→N×N，f(n)=＜n，n+1＞ f3：N→N，f(x)=x mod 3，x除以3的余数则下面说法正确的是( )。A．f1和f2是单射但不是满射函数B．f1和f3都是满射函数C．f2是双射函数D．以上说法全都是错误的

3.若已知f1(t)的拉氏变换F1(s)=1／s,则f(t)=f1(t)的拉氏变换F(s)=()。

4.设f(x)=1/x，则f(f(x)）=______

更多“设f(x)=sin2t+cost+arctant，则f1(t)=( )。”相关问题

第1题：

设时域信号 x(t)的频谱为 X(f),则时域信号( )的频谱为 X(f＋f0)。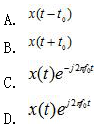

答案C
第2题：

设F1(x)与F2(x)分别为随机变量X1与X2的分布函数。为使F(x)=aF1(x)-bF2(x)成为某一随机变量的分布函数，则a与b分别是：

答案：A
解析：
第3题：

设F1(x)与F2(x)为两个分布函数，其相应的概率密度f1(x)与f2(x)是连续函数，则必为概率密度的是

A.Af1(x)f2(x)
B.2f2(x)F1(x)
C.f1(x)F2(x)
D.f1(x)F2(x)+f2(x)f1(x)

答案：D
解析：
第4题：

已知直角坐标描述的点的运动方程为X=f1（t），y=f2（t），z=f3（t），则任一瞬时点的速度、加速度即可确定。

正确答案:正确
第5题：

设X₁，X₂是任意两个相互独立的连续型随机变量，它们的概率密度分别为f₁（x）与f₂（x），分布函数分别为F₁（x）与F₂（x），则（）
- A、f₁（x）+f₂（x）必为某一随机变量的概率密度
- B、f₁（x）f₂（x）必为某一随机变量的概率密度
- C、F₁（x）+F₂（x）必为某一随机变量的分布函数
- D、F₁（x）F₂（x）必为某一随机变量的分布函数
正确答案:D
第6题：

若f（t）=f1（t）*f2（t），则有f（t）=f1（2t）*f2（2t）。

正确答案:错误
第7题：

设：y（t）=f₁（t）*f₂（t）写出：y′（t）= （）*（）

正确答案:f′₁(t)；f₂(t)
第8题：

设y=f（t），t=φ（x）都可微，则dy=（）。
- A、f＇（t）dt
- B、φ＇（x）dx
- C、f＇（t）φ＇（x）dt
- D、f＇（t）dx
正确答案:A
第9题：

Iff1（t）←→F1（jω），f2（t）←→F2（jω），Then（）
- A、f1（t）*f2（t）←→F1（jω）F2（jω）
- B、f1（t）+f2（t）←→F1（jω）F2（jω）
- C、f1（t）f2（t）←→F1（jω）F2（jω）
- D、f1（t）/f2（t）←→F1（jω）/F2（jω）
正确答案:A
第10题：

设发射信号的频率为f1，接收信号的频率为f2。若发射机作离开接收机的运动，则（）。
- A、f1＜f2
- B、f1＞f2
- C、f1=f2
- D、f1≤f2
正确答案:B
第11题：

单选题
Iff1（t）←→F1（jω），f2（t）←→F2（jω），Then（）
A
f1（t）*f2（t）←→F1（jω）F2（jω）
B
f1（t）+f2（t）←→F1（jω）F2（jω）
C
f1（t）f2（t）←→F1（jω）F2（jω）
D
f1（t）/f2（t）←→F1（jω）/F2（jω）

正确答案： A
解析：暂无解析
第12题：

单选题
设y1（x）是方程y′＋P（x）y＝f1（x）的一个解，y2（x）是方程y′＋P（x）y＝f2（x）的一个解，则y＝y1（x）＋y2（x）是方程（　　）的解。
A
y′＋P（x）y＝f₁（x）＋f₂（x）
B
y＋P（x）y′＝f₁（x）－f₂（x）
C
y＋P（x）y′＝f₁（x）＋f₂（x）
D
y′＋P（x）y＝f₁（x）－f₂（x）

正确答案： A
解析：
根据题意可知，y₁′＋P（x）y₁＝f₁（x），y₂′＋P（x）y₂＝f₂（x）。两式相加得（y₁′＋y₂′）＋P（x）（y₁＋y₂）＝f₁（x）＋f₂（x）。则可发现y＝y₁＋y₂是方程y′＋P（x）y＝f₁（x）＋f₂（x）的解。
第13题：

设f(x)=则f{f［f(x)］)等于().

答案：B
解析：
第14题：

设y=f(t)，t=φ(x)都可微，则dy=( )。

A.f′(t)dt
B.φ′(x)dx
C.f′(t)φ′(x)dt
D.f′(t)dx

答案：A
解析：
第15题：

设发射信号的频率为f1，接收信号的频率为f2。现发射机向着接收机靠近运动，则（）。
- A、f1＜f2
- B、f1＞f2
- C、f1=f2
正确答案:A
第16题：

设F₁（x）与F₂（x）为两个分布函数，其相应的概率密度f₁（x）与f₂（x）是连续函数，则必为概率密度的是（）
- A、f₁（x）f₂（x）
- B、2f₂（x）F₁（x）
- C、f₁（x）F₂（x）
- D、f₁（x）F₂（x）+f₂（x）F₁（x）
正确答案:D
第17题：

若f1（t）=u（t+1）-u（t-1），f2（t）=u（t-1）-u（t-2），则f1（t）*f2（t）的非零值区间为（）。

正确答案:（0，3）
第18题：

已知f₁（t）=u（t+1）-u（t-1），f₂=u（t-1）-（t-2），则f₁（t）*f₂（t）的非零值区间为（0，3）。

正确答案:正确
第19题：

设f₁（x）和f₂（x）为二阶常系数线性齐次微分方程y″+py′+g=0的两个特解，若由f₁（x）和f₂（x）能构成该方程的通解，下列哪个方程是其充分条件（）？
- A、f₁（x）·f′₂（x）-f₂（x）f′₁（x）=0
- B、f₁（x）·f′₂（x）-f₂（x）·f′₁（x）≠0
- C、f₁（x）f′₂（x）+f₂（x）·f′₁（x）=0
- D、f₁（x）f′₂（x）+f₂（x）f′₁（x）≠0
正确答案:B
第20题：

已知f1（t）=u（t+1）-u（t-1），f2（t）=u（t-1）-u（t-2），则f1（t）*f2（t）的非零值区间为（0，3）。

正确答案:正确
第21题：

设F₁（x）与F₁（x）分别为随机变量X₁与X₂的分布函数，若函数F（x）=aF₁（x）-bF₂（x）是某随机变量的分布函数，则必有（）
- A、a=3/5，b=-2/5
- B、a=-3/5，b=2/5
- C、a=1/2，b=3/2
- D、a=1/2，b=-3/2
正确答案:A
第22题：

单选题
设f1（x），f2（x）是二阶线性齐次方程y″＋p（x）y′＋q（x）y＝0的两个特解，则c1f1（x）＋c2f2（x）（c1，c2是任意常数）是该方程的通解的充要条件为（　　）。
A
f₁（x）f₂′（x）－f₂（x）f₁′（x）＝0
B
f₁（x）f₂′（x）＋f₁′（x）f₂（x）＝0
C
f₁（x）f₂′（x）－f₁′（x）f₂（x）≠0
D
f₁′（x）f₂（x）＋f₂（x）f₁（x）≠0

正确答案： A
解析：
要使c₁f₁（x）＋c₂f₂（x）是方程y″＋p（x）y′＋q（x）y＝0的通解，则须满足f₁（x），f₂（x）线性无关，即ψ（x）＝f₁（x）/f₂（x）≠k（k为常数）。则ψ′（x）＝[f₁′（x）f₂（x）－f₁（x）f₂′（x）]/f₂²（x）≠0，即f₁′（x）f₂（x）－f₁（x）f₂′（x）≠0。
第23题：

单选题
设y=f（t），t=φ（x）都可微，则dy=（）。
A
f＇（t）dt
B
φ＇（x）dx
C
f＇（t）φ＇（x）dt
D
f＇（t）dx

正确答案： D
解析：暂无解析

itgle.com

设f(x)=sin2t+cost+arctant，则f1(t)=( )。

题目

相似考题

更多“设f(x)=sin2t+cost+arctant，则f1(t)=( )。”相关问题

相关内容