itgle.com

设平面方程x+y+Z+1=0，直线的方程是l-x=y+1= z，则直线与平面： (A)平行 （B)垂直 (C)重合 (L)相交但不垂直

题目
设平面方程x+y+Z+1=0，直线的方程是l-x=y+1= z，则直线与平面：
(A)平行 （B)垂直 (C)重合 (L)相交但不垂直

相似考题

1.设平面经过点(1，0，－1)且与平面4x－y+2z－8=0平行，则平面π的方程为____。

2.1. 设直线L的方程为则L的参数方程是（　　）。

3.下列平面中，平行于且与yOz坐标面非重合的平面方程是（　　）。A． y＋z＋1＝0B． z＋1＝0C． y＋1＝0D． x＋1＝0

4.设平面方程为x+y+z+1=0，直线方程为1－x=y+1=z，则直线与平面： A.平行 B.垂直 C.重合 D.相交但不垂直

更多“设平面方程x+y+Z+1=0，直线的方程是l-x=y+1= z，则直线与平面： ”相关问题

  • 第1题：

    设平面π的方程为3x-4y-5z-2=0，以下选项中错误的是:
    A.平面π过点(-1，0，-1)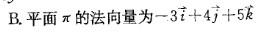

    C.平面π在Z轴的截距是-2/5
    D.平面π与平面-2x-y-2z+2=0垂直


    答案：D
    解析：

  • 第2题：

    设平面π的方程为2 x - 2 y +3 = 0，以下选项中错误的是：

    (A）平面π的法向量为i- j
    (B)平面π垂直于z轴
    (C)平面π平行于z轴
    （D）平面π与xoy面的交线为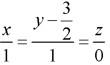


    答案：B
    解析：
    平面的方程：
    设平面II过点M0(x0,y0,zo)，它的一个法向量n={A,B,C},平面II的方程为
    A(x-x0)+B(y-y0)+C(z-z0)=0
    此方程成为平面的点法式方程
    平面的一般方程为Ax+By+Cz+D=0
    期中n={A,B,C}为该平面的法向量
    设一平面与轴分别交于P(a,0,0)，Q（0，b，0）和R(0，0，c)三点（期中a≠0，b≠0,≠0),则该平面的方程为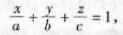此方程称为平面的截距距式方程，a,b,c依次称为平面在x,y,z轴上的截距。
    对于一些特殊的三元一次方程.应该熟悉它们的图形的特点如.在方程
    Ax By+ Cz +D=0
    中，当D=0时,方程表示一个通过原点的平面：当A=0时,方程表示一个平行于x轴的平面； 当A=B=0时,方程表示一个平行于xOy面的平面.类似地,可得其他情形的结论.

  • 第3题：

    已知平面π过点(1，1，0)、(0，0，1)、(0，1，1)，则与平面π垂直且过点(1，1，1)的直线的对称方程为 ( )。



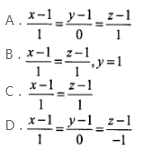    答案：B
    解析：
    平面π的法向量所求直线的方向向量为i+k，故应选B。@##

  • 第4题：

    设平面π的方程为2x-2y+3 = 0，以下选项中错误的是：
    A.平面π的法向量为i-j
    B.平面Π垂直于z轴
    C.平面Π平行于z轴


    答案：B
    解析：

  • 第5题：

    已知平面π过点M1(1，1，0)，M2(0，0，1)，M3(0，1，1)，则与平面π垂直且过点(1，1，1)的直线的对称方程为：



    答案：A
    解析：
    提示 求出过M1，M2，M3三点平面的法线向量。



    @##

  • 第6题：

    试求通过点Mo(一1，0，4)，垂直于平面Ⅱ：3x一4y-10=0，且与直线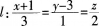
    平行的平面方程。


    答案：
    解析：
    平面Ⅱ的法向量m=（3-4，1)，直线Z的方向向量l=(3，l，2)，所以所求平面的法向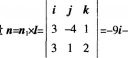

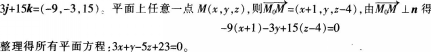
  • 第7题：

    设直线的方程为x=y-1=z， 平面的方程为x-2y+z=0，则直线与平面（ ）。
    A.重合 B.平行不重合 C.垂直相交 D.相交不垂直


    答案：B
    解析：
    正确答案为B。
    提示：直线的方向向量为s = (1，1，1)，平面的法向量为n= (1，-2，1)，s·n = 1-2 + 1 = 0,这两个向量垂直，直线与平面平行，又直线上的点(0，1，0)不在平面上，故直线与平面不重合。

  • 第8题：

    在同一平面内，直线与圆弧相切，计算切点坐标的方法是（）。

    • A、将直线方程与圆方程联立求公共解
    • B、将直线方程代入圆方程求解
    • C、将圆方程代入直线方程求解
    • D、将两个方程相加消元求解

    正确答案:A

  • 第9题：

    过点（4，-1，3）且平行于直线L：（x-3）/2=y=（z-1）/5的直线方程为（）.

    • A、（x-4）/2=（y+1）/0=（z-3）/5
    • B、（x-4）/2=（y+1）/1=（z-3）/5
    • C、（x+4）/2=（y-1）/0=（z+3）/5
    • D、（x+4）/2=（y-1）/1=（z+3）/5

    正确答案:B

  • 第10题：

    单选题
    通过直线x=2t-1，y=3t+2，z=2t-3和直线x=2t+3，y=3t-1，z=2t+1的平面方程为（）。
    A

    x-z-2=0

    B

    x+z=0

    C

    x-2y+z=0

    D

    x+y+z=1


    正确答案： D
    解析： 令t=0，点（-1，2，-3），（3，-1，1）在直线上，经验证它们也在平面（A）上。

  • 第11题：

    单选题
    设平面∏位于平面x－2y＋z－2＝0和平面x－2y＋z－6＝0之间，且将二平面间的距离分成1：3，则∏之方程为（　　）。
    A

    x－2y＋z－5＝0或x－2y＋z－3＝0

    B

    x＋2y＋z＋8＝0

    C

    x＋2y－4z＝0

    D

    x－2y＋z－8＝0


    正确答案： A
    解析：
    本题采用排除法较为简单。由于B、C两项所给出的平面方程的各项系数与已知平面不同，故它们与已知平面不平行，则可排除B、C项；D项平面与已知平面平行，但是不在两平面之间（可由常数项－8∉（－2，－6）判断出）。

  • 第12题：

    问答题
    求过点M（－1，0，1）且垂直于直线（x－2）/3＝（y＋1）/（－4）＝z/1又与直线（x＋1）/1＝（y－3）/1＝z/2相交的直线方程。

    正确答案：
    过点M(-1,0,1)且垂直于直线(x-2)/3=(y+1)/(-4)=z/1的平面方程为3x-4y+z+2=0。该平面与直线(x+1)/1=(y-3)/1=z/2的交点为(12,16,26),则该交点与点M(-1,0,1)形成的直线方程为(x+1)/13=y/16=(z-1)/25,即为所求。
    解析： 暂无解析

  • 第13题：

    设直线方程为x=y-1=z，平面方程为x-2y+z=0，则直线与平面：
    A.重合 B.平行不重合
    C.垂直相交 D.相交不垂直


    答案：B
    解析：
    从而知直线//平面或直线与平面重合；再在直线上取一点（0,1,0），验证该点是否满足平面方程。

  • 第14题：

    设平面π的方程为3x －4y －5z －2 = 0，以下选项中错误的是：
    (A)平面π过点（－1，0，－1）
    (B)平面π的法向量为－3i + 4 j + 5k


    (D) 平面π与平面－2 x －y －2 z + 2 = 0垂直


    答案：D
    解析：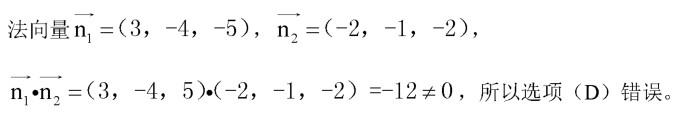

  • 第15题：

    设平面方程:x + y + z-1 = 0，直线的方程是1-x = y + 1=z，则直线与平面：
    A.平行 B.垂直 C.重合 D.相交但不垂直


    答案：D
    解析：

  • 第16题：

    设直线L过A(1，0，0)，B(0，1，1)两点，将L绕z轴旋转一周得到曲面∑，∑与平面z=0，z=2所围成的立体为Ω.
    　　(Ⅰ)求曲面∑的方程；
    　　(Ⅱ)求Ω的形心坐标.


    答案：
    解析：
    【分析】利用定义求旋转曲面∑的方程；利用三重积分求Ω的形心坐标.

  • 第17题：

    在平面直角坐标系中，以坐标原点0为极点，x轴的正半轴为极轴建立极坐标系。已知 点A的极坐标为．直线Z的极坐标方程为且点A在直线Z上。
    (1)求。的值及直线Z的直角坐标方程；
    (2)圆C的参数方程为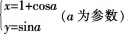试判断直线Z与圆C的位置关系。


    答案：
    解析：
    所以直线l与圆C相交。

  • 第18题：


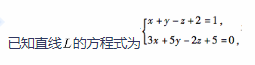
    平面Ⅱ的方程为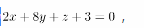

    则直线 与平面Ⅱ的位置关系是( )。


    A.平行
    B.直线在平面内
    C.垂直
    D.相交但不垂直

    答案：A
    解析：
    本题主要考查直线与平面的位置关系的判定。

  • 第19题：

    已知平面π过点(1,1，0)、(0,0,1), (0,1,1),则与平面π垂直且过点(1,1,1)的直线的对称式方程为（ ）。


    答案：B
    解析：
    正确答案是B。
    提示：平面π的法向量，所求直线的方向向量为i+k ,故应选B。

  • 第20题：

    设直线的方程为x=y-1=z，平面的方程为x-2y+z=0，则直线与平面（）。

    • A、重合
    • B、平行不重合
    • C、垂直相交
    • D、相交不垂直

    正确答案:B

  • 第21题：

    单选题
    设平面α平行于两直线x/2＝y/（－2）＝z及2x＝y＝z，且与曲面z＝x2＋y2＋1相切，则α的方程为（　　）。
    A

    4x＋2y－z＝0

    B

    4x－2y＋z＋3＝0

    C

    16x＋8y－16z＋11＝0

    D

    16x－8y＋8z－1＝0


    正确答案： B
    解析：
    由平面α平行于两已知直线可得，平面α的法向量为：n＝（2，－2，1）×（1，2，2）＝－3（2，1，－2）。设切点为（x0，y0，z0），则切点处曲面的法向量为（2x0，2y0，－1），故2/（2x0）＝1/（2y0）＝（－2）/（－1），由此解得x0＝1/2，y0＝1/4，从而z0＝x02＋y02＋1＝21/16，因此α的方程为：2（x－1/2）＋（y－1/4）－2（z－21/16）＝0，即16x＋8y－16z＋11＝0。

  • 第22题：

    单选题
    设直线方程为x=y-1=z，平面方程为x-2y+z=0，则直线与平面（　　）。[2011年真题]
    A

    重合

    B

    平行不重合

    C

    垂直相交

    D

    相交不垂直


    正确答案： C
    解析：
    直线的方向向量s＝（1，1，1），平面的法向向量n＝（1，－2，1），其向量积s·n＝1－2＋1＝0，则这两个向量垂直，即直线与平面平行。又该直线上的点（0，1，0）不在平面上，故直线与平面不重合。

  • 第23题：

    单选题
    设直线的方程为x=y-1=z，平面的方程为x-2y+z=0,则直线与平面（ ）
    A

    重合

    B

    平行不重合

    C

    垂直相交

    D

    相交不垂直


    正确答案： C
    解析：

相关内容