itgle.com

设A是n阶矩阵，矩阵A的第1列的2倍加到第2列，得矩阵B，则以下选项中成立的是( )。A.B的第1列的-2倍加到第2列得A B.B的第1行的-2倍加到第2行得A C.B的第2行的-2倍加到第1行得A D.B的第2列的-2倍加到第1列得A

题目
设A是n阶矩阵，矩阵A的第1列的2倍加到第2列，得矩阵B，则以下选项中成立的是( )。

A.B的第1列的-2倍加到第2列得A
B.B的第1行的-2倍加到第2行得A
C.B的第2行的-2倍加到第1行得A
D.B的第2列的-2倍加到第1列得A
相似考题

1.设A是3阶矩阵，矩阵A的第1行的2倍加到第2行，得矩阵B，则下列选项中成立的是( )。A.B的第1行的-2倍加到第2行得A B.B的第1列的-2倍加到第2列得A C.B的第2行的-2倍加到第1行得A D.B的第2列的-2倍加到第1列得A

2.设A为3阶矩阵，将A的第2行加到第1行得B，再将B的第1列的-1倍加到第2列得C，记，则（ ?）

3.设A是一个n阶矩阵，那么是对称矩阵的是（ ）.

4.设A是3阶方阵，将A的第1列与第2列交换得B,再把B的第2列加到第3列得C, 则满足AQ=C的可逆矩阵Q为

更多“设A是n阶矩阵，矩阵A的第1列的2倍加到第2列，得矩阵B，则以下选项中成立的是( )。”相关问题

  • 第1题：

    设A是3阶矩阵，矩阵A的第1行的2倍加到第2行，得矩阵B，则下列选项中成立的是：

    A. B的第1行的一2倍加到第2行得A
    B. B的第1列的一2倍加到第2列得A
    C. B的第2行的一2倍加到第1行得A
    D. B的第2列的一2倍加到第1列得A

    答案：A
    解析：
    由题目给出的运算写出行列式，验证还原到原行列式时应用哪一种运算方法。

  • 第2题：

    设N阶矩阵A与对角矩阵合同,则A是().

    A.可逆矩阵
    B.实对称矩阵
    C.正定矩阵
    D.正交矩阵

    答案：B
    解析：

  • 第3题：

    设A是3阶方阵，将A的第1列与第2列交换得B，再把B的第2列加到第3列得C，则满足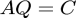的可逆矩阵Q为（ ?）.



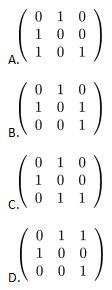    答案：D
    解析：

  • 第4题：

    设A，B是n阶矩阵，且B≠0，满足AB=0，则以下选项中错误的是：


    答案：D
    解析：
    解根据矩阵乘积秩的性质，AB=0，有r(A)+r(B)≤n成立，选项A正确。AB =0，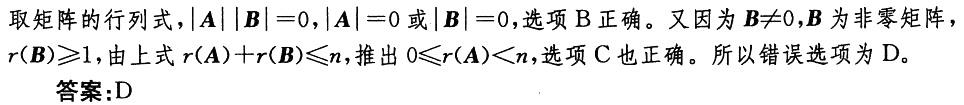

  • 第5题：

    设A为n阶非奇异矩阵，α为n维列向量，b为常数.记分块矩阵.其中A*是矩阵A的伴随矩阵，E是n阶单位矩阵. （1）计算并化简PQ； （2）证明：矩阵Q可逆的充分必要条件是.


    答案：
    解析：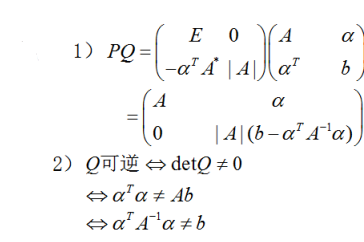

  • 第6题：

    设a为N阶可逆矩阵，则（ ）.《》（ ）


    答案：C
    解析：

  • 第7题：

    设A是m阶矩阵，B是n阶矩阵，行列式等于（ ）。


    答案：D
    解析：

  • 第8题：

    设A为n阶方阵，A*是A的伴随矩阵，则||A|A*|等于（ ）.



    答案：D
    解析：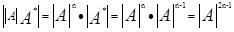

  • 第9题：

    设A为n阶可逆矩阵，则（-A）的伴随矩阵（-A）*等于（）。

    • A、-A*
    • B、A*
    • C、（-1）nA*
    • D、（-1）n-1A*

    正确答案:D

  • 第10题：

    单选题
    （2010）设A是3阶矩阵，矩阵A的第1行的2倍加到第2行，得矩阵B，则下列选项中成立的是：（）
    A

    B的第1行的-2倍加到第2行得A

    B

    B的第1列的-2倍加到第2列得A

    C

    B的第2行的-2倍加到第1行得A

    D

    B的第2列的-2倍加到第1列得A


    正确答案： B
    解析： 暂无解析

  • 第11题：

    设n阶矩阵A与对角矩阵相似,则().

    A.A的n个特征值都是单值
    B.A是可逆矩阵
    C.A存在n个线性无关的特征向量
    D.A一定为n阶实对称矩阵

    答案：C
    解析：
    矩阵A与对角阵相似的充分必要条件是其有n个线性无关的特征向量，A有n个单特征值只是其可对角化的充分而非必要条件，同样A是实对称阵也是其可对角化的充分而非必要条件，A可逆既非其可对角化的充分条件，也非其可对角化的必要条件，选(C).

  • 第12题：

    设A为m×n矩阵，C是n阶可逆矩阵，矩阵A的秩为r1，矩阵B=AC的秩为r，则



    答案：C
    解析：

  • 第13题：

    设为3阶矩阵，将的第2列加到第1列得矩阵，再交换的第2行与第3行得单位矩阵，记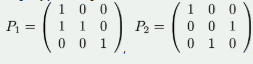，，则A=（ ）



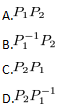    答案：D
    解析：

  • 第14题：

    设A为n（n≥2）阶可逆矩阵，交换A的第1行与第2行得矩阵B，分别为A，B的伴随矩阵，则（　　）。

    A．交换A的第1列与第2列得B
    B．交换A的第1行与第2行得B
    C．交换A的第1列与第2列得-B
    D．交换A的第1行与第2行得-B

    答案：C
    解析：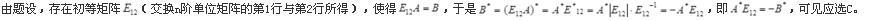

  • 第15题：

    设A是3阶矩阵,交换A的1,2列得B,再把B的第2 列加到第3 列上,得C.求Q,使得C=AQ.


    答案：
    解析：

  • 第16题：

    设A为3阶矩阵，将A的第2列加到第l列得矩阵曰，再将曰的第2行与第3行交换得

    A. P1p2
    B.P－11 P2
    C.P2P1
    D.P2P一11

    答案：C
    解析：
    由于将A的第2列加到第l列得矩阵曰，

  • 第17题：

    设A是3阶矩阵，矩阵A的第1行的2倍加到第2行，得矩阵B,则以下选项中成立的是( )。
    A. B的第1行的-2倍加到第2行得A B. B的第1列的-2倍加到第2列得A
    C.B的第2行的-2倍加到第1行得A D. B的第2列的-2倍加到第1列得A


    答案：A
    解析：
    提示：B的第1行的-2倍加到第2行得矩阵A。

  • 第18题：

    设A是3阶矩阵，矩阵A的第1行的2倍加到第2行，得矩阵B，则以下选项中成立的是（）。

    • A、B的第1行的-2倍加到第2行得A
    • B、B的第1列的-2倍加到第2列得A
    • C、B的第2行的-2倍加到第1行得A
    • D、B的第2列的-2倍加到第1列得A

    正确答案:A

  • 第19题：

    单选题
    设A是3阶矩阵，矩阵A的第1行的2倍加到第2行，得矩阵B，则以下选项中成立的是（）。
    A

    B的第1行的-2倍加到第2行得A

    B

    B的第1列的-2倍加到第2列得A

    C

    B的第2行的-2倍加到第1行得A

    D

    B的第2列的-2倍加到第1列得A


    正确答案： C
    解析： 暂无解析

相关内容