itgle.com

在棱长为1的正方体上切下两个角，所形成的两个截面为大小相等的正三角形。两个角组成了一个六面体，六面体体积为原正方体体积的1/24，则六面体表面积为原正方体表面积的：A.1/4 B.1/6 C.1/8 D.1/10

题目
在棱长为1的正方体上切下两个角，所形成的两个截面为大小相等的正三角形。两个角组成了一个六面体，六面体体积为原正方体体积的1/24，则六面体表面积为原正方体表面积的：

A.1/4
B.1/6
C.1/8
D.1/10
相似考题

1.一个正方体的棱长总和是60分米，它的棱长是（ ），表面积是（ ），体积是（ ）。

2.正方体的棱长为1m,它的体积为()。A、1m3B、2m3C、3m3D、4m3

3.如果把一个体积为125立厘米的正方体铁块切割成体积相等的8个小正方体，则每个小正方体铁块的表面积是( )。A．6.25平方厘米B．15.625平方厘米C．16.5平方厘米D．37.5平方厘米

4.把一个棱长6cm的正方体切成棱长2cm的小正方体。可以得到多少个小正方体？表面积增加了多少？

参考答案和解析
答案：C
解析：
由题意知切下的角是底面为正三角形、侧面为三个等腰直角三角形的三棱锥，设切下角的直角边为ｘ，则六面体体积＝2×三棱锥体积＝2×(1/3)×(ｘ2/2)×ｘ＝1/24，解得ｘ＝1/2。所以六面体每个面是直角边为1/2的等腰直角三角形，六面体的每个面相当于边长为1的正方形面积的1，所以六面体的表面积为原正方体的1/8。故本题选C。
更多“在棱长为1的正方体上切下两个角，所形成的两个截面为大小相等的正三角形。两个角组成了一个六面体，六面体体积为原正方体体积的1/24，则六面体表面积为原正方体表面积的：”相关问题

  • 第1题：

    一个正方体木块的体积为1000厘米³，现要把它锯成八块，同样大小的正方体小木块，小木块的棱长是多少？


    锯成8块之后，每小块的正方体体积为1000/8=125厘米³

     

    设小木块的棱长是x，则

    x³=125，x=5厘米

     

  • 第2题：

    如图1,正方体ABCDA′B′C′D′中,EE′∥FF′∥BB′,平面AEE′A′与平面ABB′A′成15°角,平面AFF′A′与平面ADD′A′成30°角.如果正方体的棱长为1,那么几何体AEF A′E′F′的体积等于____.


    参考答案3-√3

  • 第3题：

    某加工厂要将一个表面积为384平方厘米的正方体金属原材料切割成体积为8立方厘米的小正方体半成品，如果不计损失，这样的小正方体可以加工的个数为

    A. 64
    B. 36
    C. 27
    D. 16

    答案：A
    解析：

  • 第4题：

    一个正方体的边长为1，一只蚂蚁从其一个角出发，沿着正方体的棱形进，直到经过该正方体的每一条棱为止（经过一个顶点即算作经过该顶点所连接的3条棱）。则其最短的行进距离为（ ）。

    A. 3
    B. 4
    C. 5
    D. 6

    答案：C
    解析：
    蚂蚁行进路径如下图2所示，故本题答案为C选项。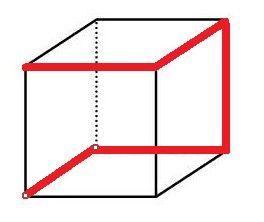

  • 第5题：

    将棱长为1的正方体的六个面的中点相连接可以得到一个八面体，则这个八面体的体积为：


    答案：A
    解析：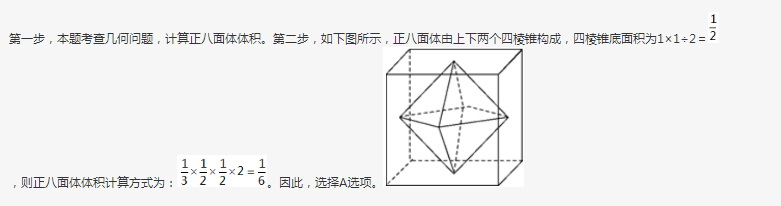

  • 第6题：

    一千个体积为1立方厘米的小正方体合在一起成为一个边长为10厘米的大正方体，大正方体表面涂油漆后再分开为原来的小正方体，这些小正方体至少有一面被油漆涂过的数目是( )个。

    A.490
    B.488
    C.484
    D.480

    答案：B
    解析：
    分析：没有涂色的小正方体都在大正方体的内部，由此先借助正方体的体积公式求出没有涂色的小正方体的个数即可解答．

    解答：解：没有涂色的小正方体：

    （10-2）×（10-2）×（10-2）=8×8×8=512（个），

    所以至少一面涂色的小正方体：1000-512=488（个）

  • 第7题：

    将一个棱长为整数的正方体零件切掉一个角，截面是面积为100√3的三角形。问其棱长最小为多少？

    A. 15
    B. 10
    C. 8
    D. 6

    答案：A
    解析：
    正方体截出一个三角形截面，最大为过三条面对角线的正三角形，正三角形面积为100√3，则正三角形的边长为20，则正方体的棱长最小为10√2，棱长为整数，则棱长最小取15。正确答案为A。

  • 第8题：

    如图，A，B是棱长为1的正方体的两个顶点，将正方体按图中所示展开，则在展开图中A，B两点间的距离为( )。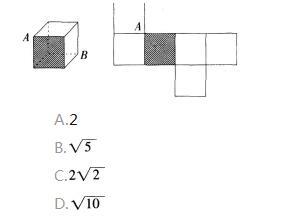


    答案：B
    解析：

  • 第9题：

    有大小两个正方体，它们棱长的比是9：5，它们表面积的比是（）

    • A、81：25
    • B、25：81
    • C、9：5
    • D、5：9

    正确答案:A

  • 第10题：

    烧结多孔砖的外形为（）

    • A、长方体
    • B、正方体
    • C、直角六面体
    • D、正八面体

    正确答案:C

  • 第11题：

    单选题
    两个对角面都是矩形的平行六面体是（　　）．
    A

    直平行六面体

    B

    长方体

    C

    正四棱柱

    D

    正方体


    正确答案： B
    解析：
    A项，直平行六面体上下两个底面为平行四边形，两对侧面均为矩形且垂直于底面；B项，长方体三个对角面均为矩形；CD两项，正四棱柱和正方体均是特殊的长方体．

  • 第12题：

    单选题
    烧结多孔砖的外形为（）
    A

    长方体

    B

    正方体

    C

    直角六面体

    D

    正八面体


    正确答案： C
    解析： 暂无解析

  • 第13题：

    如果把一个体积为125立方厘米的正方体铁块切割成体积相等的8个小正方体，则每个小正方体铁块的表面积是：

    A.6.25平方厘米

    B.15.625平方厘米

    C.16.5平方厘米

    D.37.5平方厘米


    正确答案：D

  • 第14题：

    把棱长为4的正方体分割成24个棱长为整数的正方体（且没有剩余），其中棱长为1的正方体的个数为（ ）

    A、 12

    B、 15

    C、 18

    D、 21


    正确答案：D

  • 第15题：

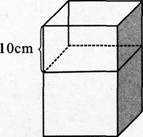
    一个正方体的高增加10cm，得到新长方体的表面积比原正方体表面积增加120cm，原正方体体积是（　　）．

    A.9cm3
    B.12cm3
    C.18cm3
    D.27cm3

    答案：D
    解析：
    如下图所示，高增加10cm后，增加的表面积为四个侧面积.设原正方体的棱长为acm，则有4×10a=120，解得a=3，则原正方体的体积为33=27cm3.

  • 第16题：

    有l25个棱长均为1的正方体，其中100个表面为白色，25个表面为蓝色。将这些正方体组成一个大正方体，表面为白色的面积至少为( )。’

    A.100
    B.97
    C.94
    D.92

    答案：D
    解析：
    题目可转化为表面为蓝色的面积至多为多少，则应把蓝色小正方体尽量放在角和棱上，这样每个小正方体可贡献3个或2个蓝色表面。因此在8个角上用去8个蓝色正方体后，在棱上再放25—8=17个，此时蓝色表面积最大为3×8+17x2=58，表面为白色的面积至少为25×6—58=92．选D。

  • 第17题：

    将一个表面积为72平方米的正方体平分为两个长方体，再将这两个长方体拼成一个大长方体，则大长方体的表面积是多少平方米？

    A.56
    B.64
    C.72
    D.84

    答案：D
    解析：
    第一步，本题考查几何问题，属于立体几何类。
    第二步，如下图所示，立方体变为长方体。正方体一个面面积为72÷6＝12（平方米），则表面积的变化为：增加了两个侧面为12×2＝24（平方米），侧面的一半减少了两个，减少了12÷2×2＝12（平方米）。故最终增加了24－12＝12（平方米），表面积为72＋12＝84（平方米）。

  • 第18题：

    把若干个体积相等的正方体拼成一个大正方体,在表面涂上红色,已知一面涂色的小正方体有96个,则两面涂色的小正方体有（ ）个

    A.48
    B.60
    C.64
    D.24
    E.32

    答案：A
    解析：
    一面涂色的小正方体位于大正方体的面上（除去機上的）,每个面有4×4=16（个）,令小正方体的边长为1,则大正方体的边长为6;两面涂色的小正方体位于大正方体的機上（除去8个角）,每条棱上有4个,故总个数为4×12=48

  • 第19题：

    把棱长为4的正方体分割成24个棱长为整数的正方体(且没有剩余），其中棱长为1的正 方体的个数为（）。
    A. 12 B. 15 C. 18 D. 21


    答案：D
    解析：
    设分割后棱长为1、2、3 .的正方体分别有x,y,z个，则有

  • 第20题：

    体积相等的球和正方体，它们的表面积的大小关系是（）。

    • A、S球＞S正方体
    • B、S球=S正方体
    • C、S球＜S正方体
    • D、不能确定

    正确答案:C

  • 第21题：

    两个质量相等的实心正方体，甲的棱长是乙的棱长的2倍，则甲的密度是乙的（）。

    • A、1/8倍
    • B、1/4倍
    • C、1/2倍
    • D、2倍

    正确答案:A

  • 第22题：

    单选题
    将一个棱长为整数的正方体零件切掉一个角，得到的截面是面积为 100倍根号3的三角形，问其棱长最小为（  ）
    A

    15

    B

    10

    C

    8

    D

    6


    正确答案： C
    解析：

  • 第23题：

    单选题
    在棱长为1的正方体上切下两个角，所形成的两个截面为大小相等的正三角形。两个角组成了一个六面体，六面体体积为原正方体体积的1/24，则六面体表面积为原正方体表面积的：
    A

    1/4

    B

    1/6

    C

    1/8

    D

    1/10


    正确答案： A
    解析：

相关内容