设X~f(x)=对X进行独立重复观察4次,用Y表示观察值大于的次数,求E(Y^2).
题目
设X~f(x)= 对X进行独立重复观察4次,用Y表示观察值大于
对X进行独立重复观察4次,用Y表示观察值大于 的次数,求E(Y^2).
的次数,求E(Y^2).
 对X进行独立重复观察4次,用Y表示观察值大于
对X进行独立重复观察4次,用Y表示观察值大于 的次数,求E(Y^2).
的次数,求E(Y^2).相似考题
更多“设X~f(x)=对X进行独立重复观察4次,用Y表示观察值大于的次数,求E(Y^2).”相关问题
-
第1题:
设随机变量X,y相互独立,且X~ ,Y~E(4),令U=X+2Y,求U的概率密度.答案:解析:
,Y~E(4),令U=X+2Y,求U的概率密度.答案:解析: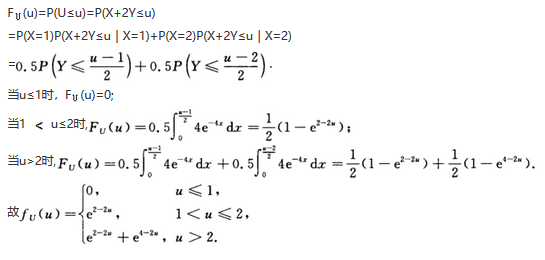
-
第2题:
设二维随机变量(X,Y)的联合密度函数为f(x,y)=
(1)求随机变量X,Y的边缘密度函数;
(2)判断随机变量X,Y是否相互独立;
(3)求随机变量Z=X+2Y的分布函数和密度函数.答案:解析:
-
第3题:
设(X,Y)的联合密度函数为f(x,y)=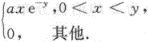
(1)求a;(2)求X,Y的边缘密度,并判断其独立性;(3)求.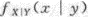 答案:解析:
答案:解析: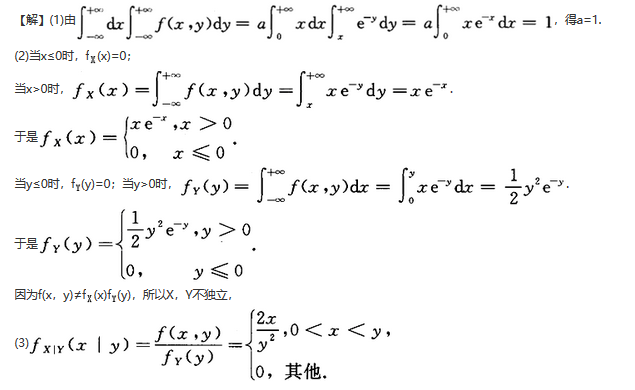
-
第4题:
设随机变量X,y相互独立,且X~P(1),y~P(2),求P(max{X,Y}≠0)及P(min{X,Y}≠0).答案:解析:
-
第5题:
设随机变量(X,Y)的联合密度为f(x,y)=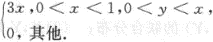 求:
求:
(1)X,Y的边缘密度;(2)P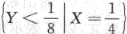 答案:解析:
答案:解析:
-
第6题:
设随机变量X~N(μ,σ^2),Y~U[-π,π],X,Y相互独立,令Z=X+Y,求fz(z).答案:解析:
-
第7题:
设(X,Y)~f(xy)=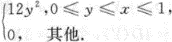
(1)判断X,Y是否独立,说明理由;(2)判断X,Y是否不相关,说明理由;
(3)求Z=X+Y的密度.答案:解析: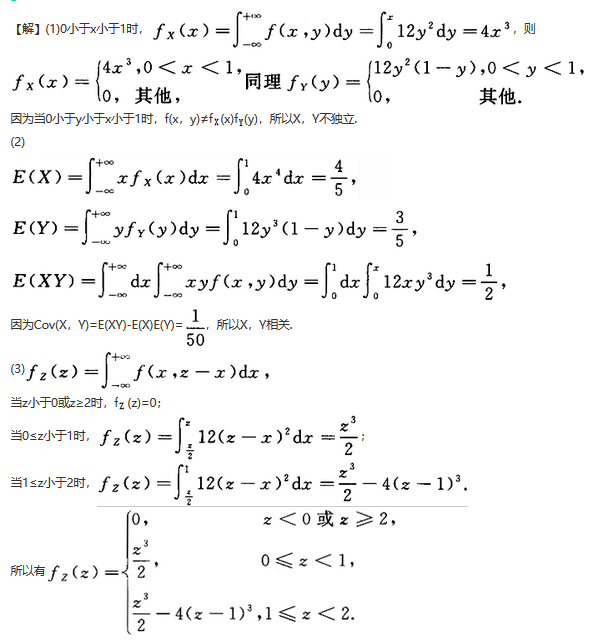
-
第8题:
设二维随机变量(X,Y)的联合密度为f(x,y)=
(1)求c;(2)求X,Y的边缘密度,问X,y是否独立?
(3)求Z=max(X,Y)的密度.答案:解析:
-
第9题:
设随机变量X的概率密度为
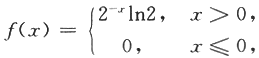
对X进行独立重复的观测,直到第2个大于3的观测值出现时停止,记Y为观测次数.
(Ⅰ)求Y的概率分布;
(Ⅱ)求EY.答案:解析:【分析】令A={对X进行一次观测得到的值大于3}.
【评注】本题类似于我们在2000年出的几何分布考题.从建模到用幂级数在其收敛区间内可逐项求导求和会有不少考生感到困难,本题要比2000年的难一些. -
第10题:
设随机变量X的概率密度为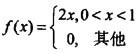 ,用Y表示对X的3次独立重复观察中事件
,用Y表示对X的3次独立重复观察中事件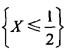 出现的次数,则P{Y=2}=( )。
出现的次数,则P{Y=2}=( )。
A.3/64 B.9/64 C.3/16 D. 9/16答案:B解析: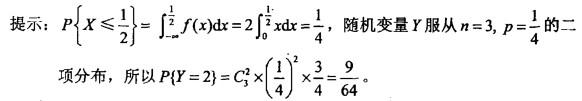
-
第11题:
设随机变量X,Y独立同分布,且X的分布函数为F(x),则Z=max{X,Y}的分布函数为()
- A、F2(x)
- B、F(x)F(y)
- C、1-[1-F(x)]2
- D、[1-F(x)][1-F(y)]
正确答案:A -
第12题:
问答题设X与Y相互独立,X的概率密度为 Y的概率密度为 求:(1)E(2X-3Y+1),D(2X-3Y+1); (2)Cov(X,Y),ρXY.正确答案:解析: -
第13题:
设随机变量X的概率密度为
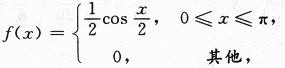
对X独立地重复观察4次,用Y表示观察值大于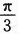 的次数,求Y^2的数学期望.答案:解析:【简解】如果将观察X理解为试验,观察值大于
的次数,求Y^2的数学期望.答案:解析:【简解】如果将观察X理解为试验,观察值大于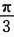 理解为试验成功,则Y表示独立地重复试验4次成功的次数,即Y~B(4,p)
理解为试验成功,则Y表示独立地重复试验4次成功的次数,即Y~B(4,p)
其中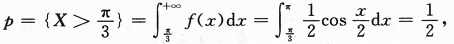

-
第14题:
设随机变量X,Y相互独立,且X~N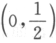 ,Y~N
,Y~N ,Z=|X-Y|,求
,Z=|X-Y|,求
E(Z),D(Z).答案:解析:
-
第15题:
设随机变量(X,Y)的联合密度函数为f(x,y)=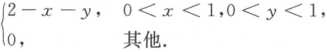 (1)求P(X>2Y);(2)设Z=X+Y,求Z的概率密度函数.
答案:解析:
(1)求P(X>2Y);(2)设Z=X+Y,求Z的概率密度函数.
答案:解析: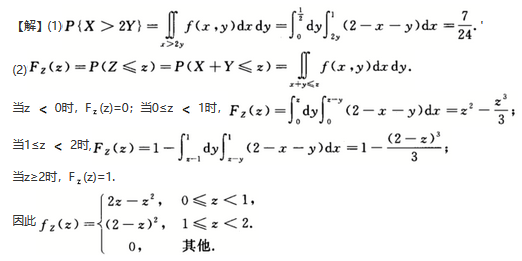
-
第16题:
设随机变量X服从参数为 的指数分布,对X独立地重复观察4次,用Y表示观察值大于3的次数,求E(Y^2).答案:解析:
的指数分布,对X独立地重复观察4次,用Y表示观察值大于3的次数,求E(Y^2).答案:解析: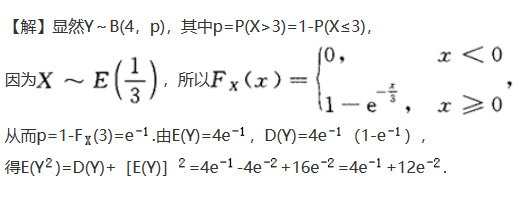
-
第17题:
设X,y的概率分布为X~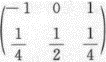 ,Y~
,Y~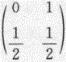 ,且P(XY=0)=1.
,且P(XY=0)=1.
(1)求(X,Y)的联合分布;(2)X,Y是否独立?答案:解析:
-
第18题:
设X,Y相互独立,且X~B ,Y~N(0,1),令U=max{X,Y},求P{1答案:解析:【解】P(U≤u)=P(max{X,Y}≤u)=P(X≤u,Y≤u)=P(X≤u)P(Y≤u),
,Y~N(0,1),令U=max{X,Y},求P{1答案:解析:【解】P(U≤u)=P(max{X,Y}≤u)=P(X≤u,Y≤u)=P(X≤u)P(Y≤u),
P(U≤1.96)=P(X≤1.96)P(Y≤1.96)=[P(X=0)+P(X=1)]P(Y≤1.96)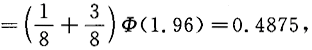
P(U≤1)=P(X≤1)P(Y≤1)=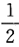 ×Ф(1)=0.4205,
×Ф(1)=0.4205,
则P(1小于U≤1.96)=P(U≤1.96)-P(U≤1)=0.067.第19题:
设(X,Y)的联合概率密度为f(x,y)=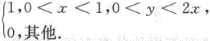 求:(1)(X,Y)的边缘密度函数;(2)2=2X-Y的密度函数.答案:解析:
求:(1)(X,Y)的边缘密度函数;(2)2=2X-Y的密度函数.答案:解析:
第20题:
设函数y=f(x)由方程y^3+xy^2+x^2y+6=0确定,求f(x)的极值.答案:解析:
第21题:
设随机变量X,Y相互独立,且X的概率分布为P{X=0)=P{X=2)= ,Y的概率密度为
,Y的概率密度为
(Ⅰ)求P{Y≤EY};
(Ⅱ)求Z=X+Y的概率密度.答案:解析:
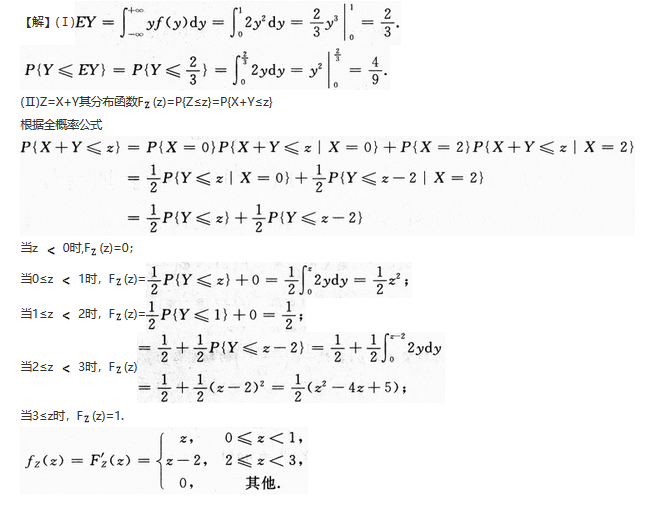
第22题:
求函数f(x,y)=e2x(x+y2+2y)的极值.?答案:解析: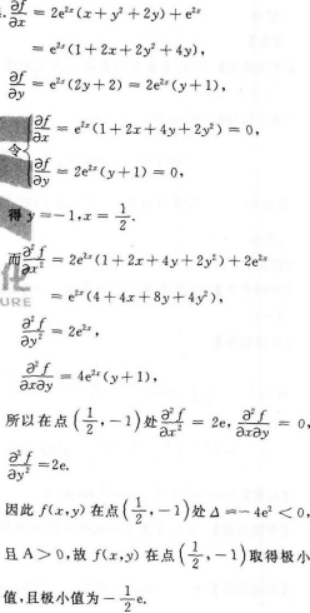
第23题:
问答题随机变量(X,Y)在矩形区域D={(x,y)|a 求:(1)联合概率密度f(x,y). (2)边缘概率密度f X(i),f Y(y). (3)X与Y是否独立?正确答案:解析:
