itgle.com

电信公司将n个人的电话资费单寄给n个人,但信封上各收信人的地址随机填写,用随机变量X表示收到自己电话资费单的人的个数,求E(X)及D(X).

题目
电信公司将n个人的电话资费单寄给n个人,但信封上各收信人的地址随机填写,用随机变量X表示收到自己电话资费单的人的个数,求E(X)及D(X).

相似考题

1.两独立随机变量X和Y都服从正态分布,且X~N(3,4),Y~N(2,9)求D(X＋Y)=()。

2.设随机变量X和Y相互独立,且X~N(2,42),Y~N(3,92),则D(X＋Y)=()

3.设随机变量和是相互独立的随机变量且都服从正态分布,X~N(3,4),Y~N(2,9),求D(3X＋4Y)=()

4.将3封信随机投入到编号为1、2、3、4的四个邮筒内,用X表示有信邮筒的最小号码,Y表示第1号邮筒中信的个数,求(X,Y)的联合分布列。

更多“电信公司将n个人的电话资费单寄给n个人,但信封上各收信人的地址随机填写,用随机变量X表示收到自己电话资费单的人的个数,求E(X)及D(X). ”相关问题

  • 第1题：

    已知随机变量x~n(10,100)。求p(7≤x<12)。

    已知随机变量x~n(10,100)。求p(7≤x<12)。


    答案：0.0319

    解析：

    p(7≤x<12)=p(x≤12)-p(x<7)

                     =p(x-10≤2)-p(x-10<-3)

                     =p(（x-10）/100≤0.02)-p(（x-10）/100<-0.03)

                      =Φ(0.05)-Φ(-0.03)

                        =Φ(0.05)-Φ(1-Φ(0.03))

                         =Φ(0.05)+Φ(0.03)-1

                         =0.5199+0.512-1=0.0319

     526(526(Φ526(

  • 第2题：

    设随机变量X～F(m,n),令P{X>Fa（m,n）}=a(0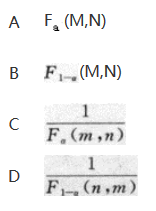


    答案：B
    解析：
    根据左、右分位点的定义，选(B).

  • 第3题：

    设随机变量X~N(0，σ2)，则对于任何实数λ，都有：
    A. P(X≤λ)=P(X≥λ)
    B.P(X≥λ)=P(X≤-λ)
    C.X-λ~N(λ,σ2-λ2)
    D.λX~N(0,λσ2)


    答案：B
    解析：

    Y=aX+b~N(au+b,a2σ2)，或利用u=0时概率密度f(x)曲线的对称性，概率(积分值)与曲边梯形面积对应判断。

  • 第4题：

    设二维随机变量(X,Y)服从二维正态分布,且X～N(1,3^2),Y～N(0,4^2),且X,Y的相
    　　关系数为－,又设Z=
    (1)求E(Z),D(Z)；(2)求；(3)X,Z是否相互独立？为什么？


    答案：
    解析：
    【解】(1)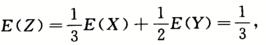

    (2)
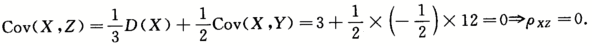
    (3)因为(X，Y)服从二维正态分布，所以Z服从正态分布，同时X也服从正态分布，又X，
    Z不相关，所以X，Z相互独立.

  • 第5题：

    设随机变量X～B（n,p）,且E(X)=5,E(X^2)=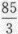,则n=_______,p=_______.


    答案：
    解析：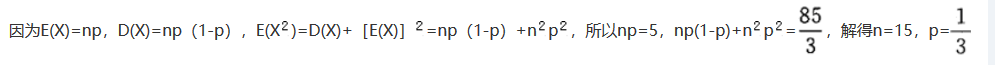

  • 第6题：

    设随机变量X～N(1,2),Y～N(-1,2),Z～N(0,9)且随机变量X,Y,Z相互独立,已知a(X+Y)2＋bZ2～χ2(n)(ab≠O),则a=_______,b=_______,Z=_______.


    答案：
    解析：
    由X～N(1，2)，Y～N(-1，2)，Z～N(0，9)，得X+Y～N(0，4)，且，故.

  • 第7题：

    设随机变量X服从正态分布N（1，2），Y服从泊松分布P（2）。求期望E=（2X—y+3）。


    答案：
    解析：
    解：本题考查一些重要分布的数字特征与参数之间的关系。E（X）=1，E（y）=2 E（2X-y+3）=2E（X）-E（y）+3=3。

  • 第8题：

    设随机变量X~N（1，22），则P{|X|≥4.56}=（）。


    正确答案:2-Φ（1.78）-Φ（2.78）

  • 第9题：

    设随机变量X～N（1，1），为使X+C～N（0，l），则常数C=（）


    正确答案:-1

  • 第10题：

    已知随机变量X~N（0， 9），那么该随机变量X的期望为（），方差为（）


    正确答案:0；9

  • 第11题：

    设随机变量X～N（1，4），则D（X）=（）


    正确答案:4

  • 第12题：

    填空题
    已知随机变量X～B（n，p），且E（X）＝1.6，D（X）＝1.28，则参数n＝____，p＝____。

    正确答案： 8,0.2
    解析：
    np＝1.6，np（1－p）＝1.28，故p＝0.2，n＝8。

  • 第13题：

    从正态分布总体X～N(μ，σ)中随机取含量为n的样本，样本均数为。从标准正态分布的随机变量是

    A．X-σ

    B．X-σX

    C．X-μσ

    D．X-μσX

    E．-μSX


    正确答案：C

  • 第14题：

    设随机变量X,Y相互独立,且X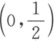～N,Y～N,则与Z=Y-X同分布的随机变量是().

    A.X-Y
    B.X+Y
    C.X-2Y
    D.Y-2X

    答案：B
    解析：
    Z=Y-X～N(1,1)，因为X-Y～N(-1,1),X+Y～N(1,1).X-2Y～N，Y-2X～N，所以选(B).

  • 第15题：

    设随机变量X?N(0，σ2)，则对于任何实数λ都有:
    (A) P(X≤λ)=P(X≥λ)(B)P(X≥λ)= P(X≤-λ)
    (C) X-λ~N(λ，σ2-λ2)(D)λX~N(0，λσ2)


    答案：B
    解析：
    解:选B。
    排除错误选项。
    X-λ~N(-λ，σ2)，选项C错误。
    λX~N(0，λ2σ2)，选项D错误。

  • 第16题：

    设随机变量X,Y相互独立,且X～N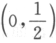,Y～N,Z=｜X-Y｜,求
    　　E(Z),D(Z).


    答案：
    解析：

  • 第17题：

    设随机变量X～N(μ,σ^2),Y～U［－π,π］,X,Y相互独立,令Z=X+Y,求fz(z).


    答案：
    解析：

  • 第18题：

    已知随机变量X服从正态分布N(μ，σ2)，设随机变量Y=2X，那么Y服从的分布是()。


    A.N(2μ，2σ2)

    B.N(4μ，4σ2)

    C.N(2μ，4σ2)

    D.N(μ，σ2)

    答案：C
    解析：
    由于随机变量X服从正态分布N(μ，σ2)，则随机变量Y=2X的均值为2μ，方差为4σ2，即Y服从的分布是N(2μ，4σ2)。

  • 第19题：

    设随机变量X~N(3，22)，且P(X>α)=P(X
    A、0


    答案：C
    解析：
    由于X为连续型随机变量，所以P(X=α)=0，己知P(X>α)=P(Xα)=0.5，即α处在正态分布的中心位置，如题可知该分布关于,=3中心对称，所以α=3。

  • 第20题：

    设随机变量X~N（3，22），若则P{X≥c}=P{X


    正确答案:3

  • 第21题：

    若随机变量X服从正态分布N（0，4），则随机变量Y=X-2的分布为（）

    • A、N（-2，4）
    • B、N（2，4）
    • C、N（0，2）
    • D、N（-2，2）

    正确答案:A

  • 第22题：

    随机抽取容量为n的样本时，n中不合格个数为X的概率为Px=n!/X!（n-X）。


    正确答案:错误

  • 第23题：

    已知随机变量X~N（0，9），那么该随机变量X的期望为（），方差为（）


    正确答案:0；9

相关内容