itgle.com

设A为三阶实对称矩阵，A的秩为2，且(Ⅰ)求A的所有特征值与特征向量；(Ⅱ)求矩阵A.

题目
设A为三阶实对称矩阵，A的秩为2，且

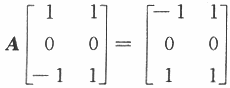
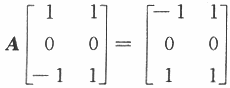
　　(Ⅰ)求A的所有特征值与特征向量；
　　(Ⅱ)求矩阵A.

相似考题

1.设三阶实对称矩阵的特征值为3,3,0,则A的秩r(A)=()A、2B、3C、4D、5

2.设三阶矩阵，若A的伴随矩阵的秩等于1，则必有A.a=b或a+2b=0 B.a=b或a+2b≠0 C.a≠b且a+2b=0 D.a≠b且a+2b≠0

3.n阶实对称矩阵A为正定矩阵，则下列不成立的是( )。A.所有k级子式为正(k=1，2，…，n) B.A的所有特征值非负 C. D.秩(A)=n

4.已知，P为三阶非零矩阵，且满足PQ=O，则A.t=6时P的秩必为1 B.t-6时P的秩必为2 C.t≠6时P的秩必为1 D.t≠6时P的秩必为2

更多“设A为三阶实对称矩阵，A的秩为2，且 ”相关问题

  • 第1题：

    设A为m×n矩阵，C是n阶可逆矩阵，矩阵A的秩为r1，矩阵B=AC的秩为r，则



    答案：C
    解析：

  • 第2题：

    设矩阵是4阶非零矩阵, 且满足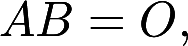证明矩阵B的秩


    答案：
    解析：

  • 第3题：

    设A为三阶实对称矩阵,A的每行元素之和为5,AX=0有非零解且λ1=2是A的特征值,
    　　对应特征向量为(-1,0,1)^T.
    　　(1)求A的其他特征值与特征向量；
    　　(2)求A.


    答案：
    解析：

  • 第4题：

    设n阶实对称矩阵A的秩为r，且满足，求 ①二次型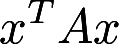的标准形； ②行列式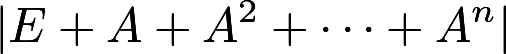的值，其中E为单位矩阵


    答案：
    解析：

  • 第5题：

    设A=图},B≠0为三阶矩阵,且BA=0,则r(B)=_______.{


    答案：1、1
    解析：
    BA=0r(A)+r(B)≤3，因为r(A)≥2，所以r(B)≤1，又因为B≠0，所以r(B)=1.

  • 第6题：

    设A是三阶实对称矩阵,r(A)=1,A^2－3A=O,设（1,1,-1）t为A的非零特征值对应的特征向量.(1)求A的特征值；(2)求矩阵A.


    答案：
    解析：

  • 第7题：

    设B≠O为三阶矩阵,且矩阵B的每个列向量为方程组的解,则k=_______,｜B｜=_______.


    答案：1、0
    解析：
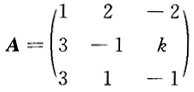    令，因为B的列向量为方程组的解且B≠0，所以AB=0且方程组有非零解，故|A|=0，解得k=1.因为AB=O，所以r(A)+r(B)≤3且r(A)≥1，于是r(B)≤2小于3，故|B|=0.

  • 第8题：

    设A为四阶实对称矩阵，且A^2+A=O.若A的秩为3，则A相似于


    答案：D
    解析：
    这是一道常见的基础题，由Aα=λα，α≠0知A^nα=λ^nα，那么对于A^2+A=0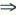(λ^2+λ)α=0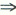λ^2+λ=0所以A的特征值只能是0或-1再由A是实对称必有A～A，而A即是A的特征值，那么由r(A)=3，可知(D)正确

  • 第9题：

    设A为三阶实对称矩阵，如果二次曲面方程
    　　
    　　在正交变换下的标准方程的图形如图所示，
    　　
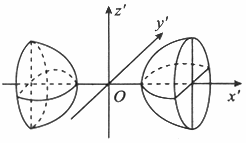
    　　则A的正特征值的个数为

    A.A0
    B.1
    C.2
    D.3

    答案：B
    解析：
    本题把线性代数与解析几何的内容有机的联系起来，首先要明白所给图形是什么曲面？其标准方程是什么？　　双叶双曲面，标准方程是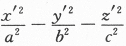：=1其次，二次型经正交变换化为标准形时，其平方项的系数就是A的特征值，所以应选(B).
    很多考生选择(C)，是不是把标准方程记成了图1}　而忽略了本题的条件是x^TAx=1.

  • 第10题：

    设A，B为三阶矩阵且A不可逆，又AB+2B=O 且r（B）=2，则 |A+4E|=

    A.8
    B.16
    C.2
    D.0

    答案：B
    解析：

  • 第11题：

    设3阶矩阵，已知A的伴随矩阵的秩为1，则a=（）。

    • A、-2
    • B、-1
    • C、1
    • D、2

    正确答案:A

  • 第12题：

    单选题
    设3阶矩阵，已知A的伴随矩阵的秩为1，则a=（）。
    A

    -2

    B

    -1

    C

    1

    D

    2


    正确答案： B
    解析： 暂无解析

  • 第13题：

    设矩阵，则A^3的秩为________


    答案：
    解析：

  • 第14题：

    设A=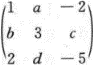,B为三阶非零矩阵,且AB=O,则r(A)=_______.


    答案：1、2
    解析：
    因为AB=0，所以r(A)+r(B)≤3，又因为B≠0，所以r(B)≥1，从而有r(A)≤2，显然A有两行不成比例，故r(A)≥2，于是r(A)=2.

  • 第15题：

    设A为m阶实对称矩阵且正定，B为m×n实矩阵，B^T为B的转置矩阵，试证：B^TAB为正定矩阵的充分必要条件是B的秩r(B)=n，


    答案：
    解析：

  • 第16题：

    设A为三阶矩阵,且｜A｜=4,则=_______.


    答案：
    解析：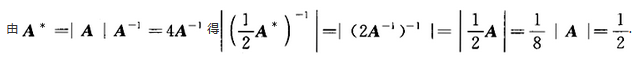

  • 第17题：

    设A为实对称矩阵,且A的特征值都大于零.证明：A为正定矩阵.


    答案：
    解析：

  • 第18题：

    设A，B为三阶矩阵，且满足方程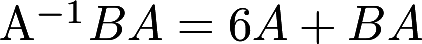.若矩阵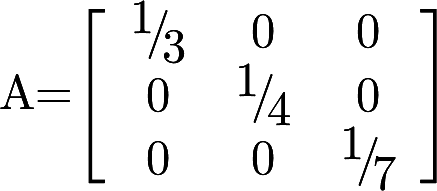,求矩阵B.


    答案：
    解析：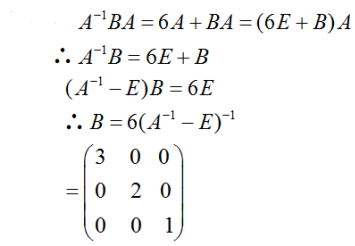

  • 第19题：

    设A为m×n矩阵，B为n×m矩阵，E为m阶单位矩阵，若AB=E，则



    A.A秩r(A)=m，秩r(B)=m
    B.秩r(A)=m，秩r(B)=n
    C.秩r(A)=n，秩r(B)=m
    D.秩r(A)=n，秩r(B)=n

    答案：A
    解析：
    本题考的是矩阵秩的概念和公式.因为AB=E是m阶单位矩阵，知r(AB)=m.又因r(AB)≤min(r(A)，r(B))，故m≤r(A)，m≤r(B). ①另一方面，A是m×n矩阵，B是n×m矩阵，又有r(A)≤m，r(B)≤m. ②比较①、②得r(A)=m，r(B)=m.所以选(A)

  • 第20题：

    设α为三维单位列向量，E为三阶单位矩阵，则矩阵E-αα^T的秩为________.


    答案：
    解析：

  • 第21题：

    设A为3阶实对称矩阵，A的秩为2，且.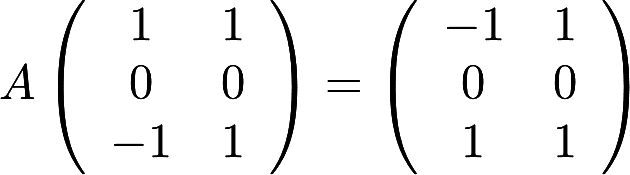 （Ⅰ）求A的特征值与特征向量； （Ⅱ）求矩阵A


    答案：
    解析：

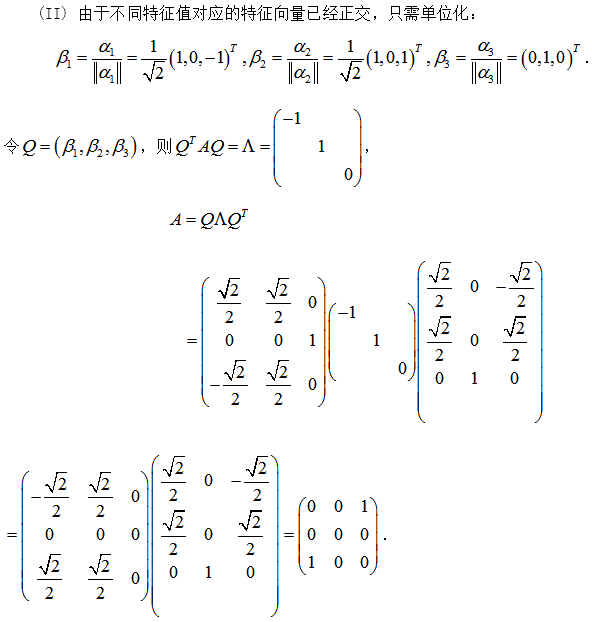
  • 第22题：

    n阶实对称矩阵A为正定矩阵，则下列不成立的是（）。

    • A、所有k级子式为正（k=1，2，…，n）
    • B、A的所有特征值非负
    • C、秩（A）=n

    正确答案:A

  • 第23题：

    填空题
    设，B为三阶非零矩阵，且AB＝0，则t＝____。

    正确答案： -3
    解析：
    由B是三阶非零矩阵，且AB＝0，知B的列向量是方程组AB＝0的解且为非零解，故|A|＝0，解得t＝－3。

相关内容