itgle.com

若三次多项式f（x）满足f（2）=f（-1）=f（1）=0,f（0）=4,则f（-2）=（ ）A.0 B.1 C.-1 D.24 E.-24

题目
若三次多项式f（x）满足f（2）=f（-1）=f（1）=0,f（0）=4,则f（-2）=（ ）

A.0
B.1
C.-1
D.24
E.-24
相似考题

1.如果f(x)对任何x都满足f(1＋x)=2f(x),且f(0)存在,f’(0)=2,则f’(1)=()。A．4B．-4C．8D．-8

2.上题中，若求P{X=a},则()A、F(a)B、F(a-0)C、F(a)-F(a-0)D、1-F(a)

3.对一路信号进行FSK调制时，若载波频率为f0，调制后的信号频率分别为f1和f2(f1＞f2)，则f0、f1、f2三者的关系是(22)。A．f2-f1=f0B．f2+f1=f0C．f1/f2=f0D．f0-f2=f1-f0

4.在Z3={0,1,2}中,求一个多项式f(x)使得f(1)=0,f(2)=0。

更多“若三次多项式f（x）满足f（2）=f（-1）=f（1）=0,f（0）=4,则f（-2）=（ ）”相关问题

  • 第1题：

    已知f(x)=x2+ax+3，若f(2+x)=f(2-x)，则f(2)=（）。

    A.0

    B.-1

    C.-2

    D.-3


    正确答案：B
    32.B【解析】由f(2+x)=f(2-x)可知该函数对称轴为x=2，而根据f(x)=x2+ax+3，可知该函数为二次函数。那么根据二次函数的性质，可知a=(-2)×1×2=-4，则f(2)=22+(-4)×2+3=-1，所以答案为B项。

  • 第2题：

    设f1（x）和f2（x）为二阶常系数线性齐次微分方程y"+py'+q=0的两个特解， 若由f1（x）和f2（x）能构成该方程的通解，下列哪个方程是其充分条件？

    A.f1（x） *f'2（x）-f2（x）f'1（x）=0
    B.f1（x） * f’2（x）-f2（x） *f'1（x）≠0
    C.f1（x）f'2（x）+f2（x）*f'1（x） =0
    D.f1（x）f'2（x）+f2（x）*f'1（x） ≠0

    答案：B
    解析：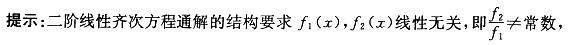

  • 第3题：

    若函数f(x)满足方程f"(x)+f'(x)-2f(x)=0及f"(x)+f(x)=2e……x，则f(x)=________.


    答案：1、e^x.
    解析：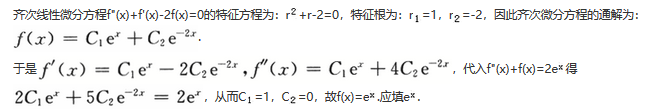

  • 第4题：

    若实值函数f定义域为全体实数，且满足任意x，y:f(x+y)=f(x)f(y)。此时，若f(8)=4，则有f(2)=( )。
    A. 0 D. 2


    答案：C
    解析：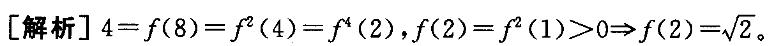

  • 第5题：

    设f(x)是R上的可导函数，且f(x)>0。若f′(x)-3x---2f(x)=0，且f(0)=1，求f(x)。


    答案：
    解析：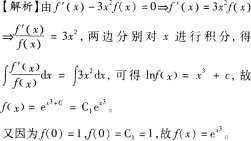

  • 第6题：

    设fˊ（-1）=1，fˊ（0）=3，fˊ（2）=4，则抛物插值多项式中x2的系数为（）。

    • A、-0.5
    • B、0.5
    • C、2
    • D、-2

    正确答案:A

  • 第7题：

    用牛顿切线法解方程f（x）=0，选初始值x0满足（），则它的解数列{xn}n=0，1，2，…一定收敛到方程f（x）=0的根。

    • A、f（x0）f″（x）>0
    • B、f（x0）f′（x）>0
    • C、f（x0）f″（x）<0
    • D、f（x0）f′（x）<0

    正确答案:A

  • 第8题：

    填空题
    设函数y＝y（x）由方程y＝f（x2＋y2）＋f（x＋y）所确定，且y（0）＝2，其中f是可导函数，f′（2）＝1/2，f′（4）＝1，则dy/dx|x＝0＝____。

    正确答案： -1/7
    解析：
    由方程y＝f（x2＋y2）＋f（x＋y）。两边对x求导得yx′＝f′（x2＋y2）（2x＋2y·yx′）＋f′（x＋y）（1＋yx′）。
    又y（0）＝2，f′（2）＝1/2，f′（4）＝1，，故y′|x＝0＝f′（4）·4y′|x＝0＋f′（2）（1＋y′|x＝0），y′|x＝0＝4y′|x＝0＋（1＋y′|x＝0）/2，解得y′|x＝0＝－1/7。

  • 第9题：

    单选题
    设f1（x），f2（x）是二阶线性齐次方程y″＋p（x）y′＋q（x）y＝0的两个特解，则c1f1（x）＋c2f2（x）（c1，c2是任意常数）是该方程的通解的充要条件为（　　）。
    A

    f1（x）f2′（x）－f2（x）f1′（x）＝0

    B

    f1（x）f2′（x）＋f1′（x）f2（x）＝0

    C

    f1（x）f2′（x）－f1′（x）f2（x）≠0

    D

    f1′（x）f2（x）＋f2（x）f1（x）≠0


    正确答案： A
    解析：
    要使c1f1（x）＋c2f2（x）是方程y″＋p（x）y′＋q（x）y＝0的通解，则须满足f1（x），f2（x）线性无关，即ψ（x）＝f1（x）/f2（x）≠k（k为常数）。则ψ′（x）＝[f1′（x）f2（x）－f1（x）f2′（x）]/f22（x）≠0，即f1′（x）f2（x）－f1（x）f2′（x）≠0。

  • 第10题：

    填空题
    设f（0）=0，f（1）=16，f（2）=46，则f[0，1]=（），f[0，1，2]=（），f（x）的二次牛顿插值多项式为（）。

    正确答案： 16,7,0+16（x-0）+7（x-0）（x-1）
    解析： 暂无解析

  • 第11题：

    问答题
    设函数f（x）在[0，1]上二阶可导，且f（0）＝f（1）＝0，证明：必∃ξ∈（0，1）使ξ2f″（ξ）＋4ξf′（ξ）＋2f（ξ）＝0。

    正确答案：
    构造函数F(x)=x2f(x),由于f(x)在[0,1]上二阶可导,则F(x)也在[0,1]上二阶可导。
    又F′(0)=[2xf(x)+x2f′(x)]x=0=0,F″(x)=2f(x)+4xf′(x)+x2f″(x)。
    故根据泰勒公式有F(1)=F(0)+F′(0)(1-0)+F″(ξ)(1-0)2/(2!)=0,其中ξ∈(0,1)。
    所以F″(ξ)/2=[2f(ξ)+4ξf′(ξ)+ξ2f″(ξ)]/2=0。
    即2f(ξ)+4ξf′(ξ)+ξ2f″(ξ)=0。
    解析： 暂无解析

  • 第12题：

    单选题
    设函数y＝y（x）由方程y＝f（x2＋y2）＋f（x＋y）所确定，且y（0）＝2，其中f是可导函数，f′（2）＝1/2，f′（4）＝1，则dy/dx|x＝0＝（　　）。
    A

    －1/2

    B

    －1/4

    C

    －1/7

    D

    －1/9


    正确答案： C
    解析：
    由方程y＝f（x2＋y2）＋f（x＋y）。两边对x求导得yx′＝f′（x2＋y2）（2x＋2y·yx′）＋f′（x＋y）（1＋yx′）。
    又y（0）＝2，f′（2）＝1/2，f′（4）＝1，故y′|x＝0＝f′（4）·4y′|x＝0＋f′（2）（1＋y′|x＝0），y′|x＝0＝4y′|x＝0＋（1＋y′|x＝0）/2，解得y′|x＝0＝－1/7。

  • 第13题：

    数学运算

    已知f(x)＝x2+ax+3，若f(2+x)＝f(2-x)，则f(2)＝( )。

    A．0

    B．-1

    C．-2

    D．3


    正确答案：B
    [解析]本题答案为B。本题属于函数问题。由f(2+x)＝f(2-x)知道函数f(x)的对称轴为x＝ 2，因此-(a/2)＝2，a＝-4。所以f(2)＝22-2×4+3＝-1。

  • 第14题：

    若f（-x）=f（x），且在（0，+∞）内f′（x）＞0，f″（x）＜0，则f（x）在（-∞，0）内（ ）。

    A.f′（x）＜0，f″（x）＜0
    B.f′（x）＜0，f″（x）＞0
    C.f′（x）＞0，f″（x）＜0
    D.f′（x）＞0，f″（x）＞0

    答案：A
    解析：
    已知在给出的（0，+∞）内，f′（x）＞0，f″（x）＜0，故在（0，+∞）上f（x）单调递增，且图形是凸的，再根据已知条件f（-x）=f（x）可知f（x）是偶函数，利用图形的对称性可得出f（x）在（-∞，0）是单调递减且也是凸的。故应该选择A。

  • 第15题：

    已知函数f(x）=f(x+4),f(0）=0，且在（—2，2）上有f'(x)=|x|,则f(19)=



    答案：C
    解析：
    由f(x）=f(x+4),知f(x)是周期为4的周期函数，故f(19)=f(-1），

  • 第16题：

    设三次多项式函数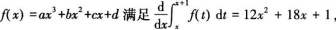则f(x)的极大值点为( )


    A.0

    B.1

    C.-1

    D.2

    答案：C
    解析：

  • 第17题：

    若f(x)为可导函数，且已知f(0) = 0，f'(0) = 2,则的值为()。
    A. 0 B. 1 C. 2 D.不存在


    答案：B
    解析：
    提示：利用积分上限函数求导和洛必达法则。

  • 第18题：

    设f（0）=0，f（1）=16，f（2）=46，则f[0，1]=（），f[0，1，2]=（），f（x）的二次牛顿插值多项式为（）。


    正确答案:16；7；0+16（x-0）+7（x-0）（x-1）

  • 第19题：

    设f1（x）和f2（x）为二阶常系数线性齐次微分方程y″+py′+g=0的两个特解，若由f1（x）和f2（x）能构成该方程的通解，下列哪个方程是其充分条件（）？

    • A、f1（x）·f′2（x）-f2（x）f′1（x）=0
    • B、f1（x）·f′2（x）-f2（x）·f′1（x）≠0
    • C、f1（x）f′2（x）+f2（x）·f′1（x）=0
    • D、f1（x）f′2（x）+f2（x）f′1（x）≠0

    正确答案:B

  • 第20题：

    单选题
    设f1（x）和f2（x）为二阶常系数线性齐次微分方程y″+py′+q=0的两个特解，若由f1（x）和f2（x）能构成该方程的通解，下列哪个方程是其充分条件？（）
    A

    f1（x）f′2（x）-f2（x）f′1（x）=0

    B

    f1（x）f′2（x）-f2（x）f′1（x）≠0

    C

    f1（x）f′2（x）+f2（x）f′1（x）=0

    D

    f1（x）f′2（x）+f2（x）f′1（x）≠0


    正确答案： C
    解析： 暂无解析

  • 第21题：

    单选题
    设f（x），g（x）具有任意阶导数，且满足f″（x）＋f′（x）g（x）＋f（x）x＝ex－1，f（0）＝1，f′（0）＝0。则（　　）。
    A

    f（0）＝1为f（x）的极小值

    B

    f（0）＝1为f（x）的极大值

    C

    （0，f（0））为曲线y＝f（x）的拐点

    D

    由g（x）才能确定f（x）的极值或拐点


    正确答案： B
    解析：
    由f″（x）＋f′（x）g（x）＋f（x）x＝ex－1，f（0）＝1，f′（0）＝0，得f″（0）＝0。f″（x）＋f′（x）g（x）＋f（x）x＝ex－1两边对x求导有
    f‴（x）＋f″（x）g（x）＋f′（x）g′（x）＋f′（x）x＋f（x）＝ex①
    可得f‴（0）＝0，①两边再次对x求导得f（4）（x）＋f‴（x）g（x）＋2f″（x）g′（x）＋f′（x）g″（x）＋f″（x）x＋2f′（x）＝ex，可得f（4）（0）＝1＞0，故f（0）＝1为f（x）的极小值。故应选（A）。

  • 第22题：

    单选题
    设函数y＝y（x）由方程y＝f（x2＋y2）＋f（x＋y）所确定，且y（0）＝2，其中f是可导函数，f′（2）＝1/2，f′（4）＝1，则dy/dx|x＝0＝（　　）。
    A

    1

    B

    －1

    C

    1/7

    D

    －1/7


    正确答案： B
    解析：
    由方程y＝f（x2＋y2）＋f（x＋y）。两边对x求导得yx′＝f′（x2＋y2）（2x＋2y·yx′）＋f′（x＋y）（1＋yx′）。
    又y（0）＝2，f′（2）＝1/2，f′（4）＝1，故y′|x＝0＝f′（4）·4y′|x＝0＋f′（2）（1＋y′|x＝0），y′|x＝0＝4y′|x＝0＋（1＋y′|x＝0）/2，解得y′|x＝0＝－1/7。

  • 第23题：

    单选题
    设fˊ（-1）=1，fˊ（0）=3，fˊ（2）=4，则抛物插值多项式中x2的系数为（）。
    A

    -0.5

    B

    0.5

    C

    2

    D

    -2


    正确答案： A
    解析： 暂无解析

相关内容