itgle.com

已知a为无理数,（a-1）（a+2）为有理数,则下列说法正确的是A.a2为有理数 B.（a+1）（a+2）为无理数 C.（a-5）2为有理数 D.（a+5）2为有理数 E.以上都不对

题目
已知a为无理数,（a-1）（a+2）为有理数,则下列说法正确的是

A.a2为有理数
B.（a+1）（a+2）为无理数
C.（a-5）2为有理数
D.（a+5）2为有理数
E.以上都不对
相似考题

1.正义：非正义（ ） A．有理数：无理数 B．早晨：今晚 C．植物：动物 D．宽恕：怨恨

2.数学理解1，2，3，4，5，6，7，8，9，10的平方根和立方根中，哪些是有理数？哪些是无理数？

3.判断题： （1）不带根号的数都是有理数； （2）两个无理数的和还是无理数。

4.–a+2(a-1)-(3a+5)

更多“已知a为无理数,（a-1）（a+2）为有理数,则下列说法正确的是”相关问题

  • 第1题：

    数学理解

    两个有理数相加、相减、相乘、相除，结果一定还是有理数吗？说明理由，两个无理数相加、相减、相乘、相除，结果一定还是无理数吗？举例说明。


    两个有理数相加、相减、相乘、相除，结果一定还是有理数！

    两个无理数相加、相减、相乘、相除，结果不一定是无理数！

  • 第2题：

    判断下列说法是否正确：

    （1）无限小数都是无理数；

    （2）无理数都是无限小数；

    （3）带根号的数都是无理数；

    （4）所有有理数都可以用数轴上的点表示，反过来，数轴上的所有点都表示有理数；

    （5）所有实数都可以用数轴上的点表示，反过来，数轴上的所有点都表示实数。


    （1）错误

    （2）正确

    （3）错误

    （4）错误

    （5）正确


  • 第3题：

    所有的有理数都是实数；所有的无理数也是实数；虚数不是实数。因此，虚数既不是有理数也不是无理数．

    (1)将上述命题符号化。

    (2)用演绎法证明其结论是否正确。


    正确答案：设Q(x):x是有理数； R(x):x是实数； N(x):x是无理数； C(x):x是虚数。 则命题可符号为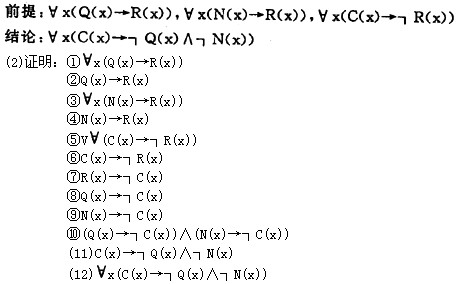： 所以结论是正确的。
    设Q(x):x是有理数； R(x):x是实数； N(x):x是无理数； C(x):x是虚数。 则命题可符号为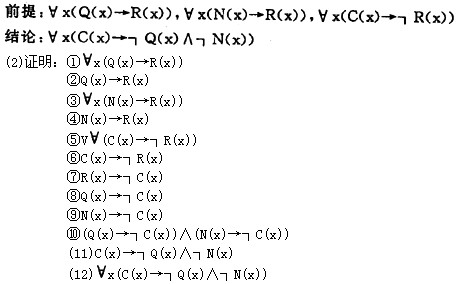： 所以结论是正确的。

  • 第4题：

    设A为可逆矩阵，则下列结论不正确的是( )。

    A、(A-1)-1=A
    B、|A-1|=|A|-1
    C、(KA)-1=KA-1(k≠0)
    D、(A')-1=(A-1)'

    答案：C
    解析：
    根据逆矩阵的性质，(A)、(B)、(D)都正确，选项(C)应为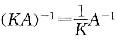

  • 第5题：

    在下列语句中：
    ①无理数的相反数是无理数；
    ②一个数的绝对值一定是非负数；
    ③有理数比无理数小；
    ④无限小数不一定是无理数.
    其中正确的是（　　）

    A、②③；
    B、②③④；
    C、①②④；
    D、②④、

    答案：C
    解析：

  • 第6题：

    “有理数与无理数统称为实数”其定义方式是（）

    • A、归纳定义
    • B、公理化定义
    • C、关系性定义
    • D、发生性定义

    正确答案:D

  • 第7题：

    古希腊数学中算术的地位受到挑战是因为（）的发现。

    • A、虚数
    • B、循环小数
    • C、无理数
    • D、有理数

    正确答案:C

  • 第8题：

    以下集合中（）的基数最小。

    • A、实数集
    • B、自然数集
    • C、无理数集
    • D、有理数集

    正确答案:B

  • 第9题：

    毕达哥拉斯学派认为万物都是（）

    • A、无理数
    • B、实数
    • C、虚数
    • D、有理数

    正确答案:D

  • 第10题：

    单选题
    引发第一次数学危机的数是（）
    A

    自然数

    B

    正整数

    C

    有理数

    D

    无理数


    正确答案： C
    解析： 暂无解析

  • 第11题：

    单选题
    已知测者纬度等于30°N，3月21日测得太阳真没方位等于92°NW，则罗经差为（）。
    A

    ＋2°

    B

    －2°

    C

    ＋1°

    D

    －1°


    正确答案： A
    解析： 暂无解析

  • 第12题：

    单选题
    毕达哥拉斯学派认为万物都是（）
    A

    无理数

    B

    实数

    C

    虚数

    D

    有理数


    正确答案： A
    解析： 暂无解析

  • 第13题：

    0，1，2，3，4，5，6，7，8，9，10的平方根及立方根中，哪些是有理数？哪些是无理数？


    （1）0,1,4,9的平方根是有理数

    （2）2,3,5,6,7,8,10的平方根是无理数

    （3）0,1,8的立方根是有理数

    （4）2,3,4,5,6,7,9,10 的立方根是无理数


  • 第14题：

    已知数0.101 001 000 100 001…，它的特点是：从左向右看，相邻的两个1之间依次多一个0。这个数是有理数还是无理数？为什么？


    解：这个数是无理数，因为这个数是无限不循环小数，属于无理数。

  • 第15题：

    ：有理数：无理数（ ）。

    A．金属：重金属

    B．直接经验：实践经验

    C．动物：植物

    D．历史：过去


    正确答案：C
    与有理数相对的是无理数，同理，与动物相对是植物。

  • 第16题：

    下列选项中，运算结果一定是无理数的是（ ）。


    A.有理数与无理数的和
    B.有理数与有理数的差
    C.无理数与无理数的和
    D.无理数与无理数的差

    答案：A
    解析：
    本题主要考查有理数和无理数的性质。（1）有理数与有理数：和、差、积、商均为有理数（求商时分母不为零）。（2）有理数与无理数：一个有理数和一个无理数的和、差均为无理数；一个非零有理数和一个无理数的积、商均为无理数。（3）无理数和无理数：和、差、积、商可能是有理数也可能是无理数。A项正确。

    B、C、D三项：均为干扰项。与题干不符，排除。

  • 第17题：

    科学童话《有理数无理数大战》的作者是（）。

    A星河

    B杨鹏

    C李毓佩

    D王梓坤


    C
    略

  • 第18题：

    已知chara=’R’；则正确的赋值表达式是（）

    • A、a=（a++）%4
    • B、a+2=3
    • C、a+=256--
    • D、a=’/078’

    正确答案:A

  • 第19题：

    第一次数学危机，实际是发现了（）的存在。

    • A、有理数
    • B、无理数
    • C、素数
    • D、无限不循环小数

    正确答案:B

  • 第20题：

    引发第一次数学危机的数是（）

    • A、自然数
    • B、正整数
    • C、有理数
    • D、无理数

    正确答案:D

  • 第21题：

    单选题
    科学童话《有理数无理数大战》的作者是（）。
    A

    星河

    B

    杨鹏

    C

    李毓佩

    D

    王梓坤


    正确答案： A
    解析： 暂无解析

  • 第22题：

    单选题
    关于“有理数”与“无理数”的数量比较，正确的一项是：（）。
    A

    有理数较多

    B

    无理数较多

    C

    一样多

    D

    无法比较


    正确答案： D
    解析： 暂无解析

  • 第23题：

    单选题
    以下集合中（）的基数最小。
    A

    实数集

    B

    自然数集

    C

    无理数集

    D

    有理数集


    正确答案： B
    解析： 暂无解析

相关内容