设 z=f(x2 - y2),则 dz 等于:(A) 2x-2y (B) 2xdx-2ydy (C) f (x2 - y2)dx (D) 2 f(x2 - y2)(xdx- ydy)
题目
相似考题
更多“设 z=f(x2 - y2),则 dz 等于:(A) 2x-2y (B) 2xdx-2ydy (C) f (x2 - y2)dx (D) 2 f(x2 - y2)(xdx- ydy)”相关问题
-
第1题:
阅读以下说明和C++代码,
[说明]
现要编写一个画矩形的程序,目前有两个画图程序:DP1和DP2,DP1用函数draw_a_line(x1,y1,x2,y2)画一条直线,DP2则用drawline(x1,x2,y1,y2)画一条直线。当实例化矩形时,确定使用DP1还是DP2。为了适应变化,包括“不同类型的形状”和“不同类型的画图程序”,将抽象部分与实现部分分离,使它们可以独立地变化。这里,“抽象部分”对应“形状”,“实现部分”对应“画图”,与一般的接口(抽象方法)与具体实现不同。这种应用称为Bridge(桥接)模式。图6-1显示了各个类间的关系。
[图6-1]

这样,系统始终只处理3个对象:Shape对象、Drawingg对象、DP1或DP2对象。以下是C++语言实现,能够正确编译通过。
[C++代码]
class DP1{
public:
static void draw_a_line(double x1,double y1,double x2,double y2){
//省略具体实现
}
};
class DP2{
public:
static void drawline(double x1,double x2,double y1,double y2){
//省略具体实现
}
};
class Drawing{
public:
(1) void drawLine(double x1,double y1,double x2,double y2)=0;
};
class V1Drawing:public Drawing{
public:
void drawLine(double x1,double y1,double x2,double y2){
DP1::draw_a_line(x1,y1,x2,y2);
}
};
class V2Drawing:public Drawing{
public:
void drawLine(double x1,double y1,double x2,double y2){
(2)
}
};
class Shape{
privatc:
(3) dp;
public:
Shape(Drawing*dp);
virtual void draw()=0;
void drawLine(double x1,double y1,double x2,double y2);
};
Shape::Shape(Drawing*dp)
{
_dp=dp;
}
void Shape::drawLine(double x1,double y1,double x2,double y2)
{ //画一条直线
(4);
}
class Rectangle:public Shape{
privatc:
double_x1,_y1,_x2,_y2;
public:
Rectangle(Drawing *dp,double x1,double y1,
double x2,double y2);
void draw();
};
Rectangle::Rectangle(Drawing*dp,double x1,double y1,double x2,double y2)
: (5)
{
_x1=x1;_y1=yl;_x2=x2;_y2=y2;
}
void Rectangle::draw()
{
//省略具体实现
}
(1)
正确答案:virtual
virtual 解析:由函数drawLine()结尾的“=0”易知,空(1)应填virtual。 -
第2题:
在下图所示的树型文件系统中,方框表示目录,圆圈表示文件,“/”表示目录名之间的分隔符,“/”在路径之首时表示根目录。假设“..”表示父目录,当前目录是Y1,那么,指定文件F2所需的相对路径是(29);如果当前目录是X2,“DEL'’表示删除命令,那么,删除文件F4的正确命令是(30)。
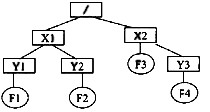
A./X1/Y2/F2
B.../X1/Y2/F2
C.X1/Y2/F2
D.../Y2/F2
正确答案:D
解析:采用多级目录结构的文件系统中;用户要访问一个文件,必须指出文件所在的路径名,路径名是从根目录开始到该文件的通路上所有各级目录名拼起来得到的。各目录名之间,目录名与文件名之间需要用分隔符隔开。例如,在MS-DOS中分隔符为“\”,在 UNIX中分隔符为“/”。绝对路径名(absolute path name)是指从根目录“/”开始的完整文件名,即它是由从根目录开始的所有目录名以及文件名构成的。采用多级目录结构提高了检索目录的速度,例如采用单级目录。查找一个文件最多需查遍系统目录文件中的所有文件目录项,平均也要查一半文件目录项。而多级目录查找一个文件最多只要查遍文件路径上根目录文件和子目录文件中的目录项。由于每访问一个文件都要使用从根目录开始搜索直到树叶的数据文件为止,包含各中间子目录的全路径名相当麻烦而且费时。为此引入相对路径(relative path name)。由于一个进程运行时访问的文件大多局限在某个范围,基于这一点,可为每个用户(或每个进程)设置一个“当前目录”,又称“工作目录”或称“值班目录”。进程对各文件的访问都相对于“当前目录”而设置路径,这称为相对路径,用相对路径可缩短搜索路径,提高目录检索的速度。可见根据题意,当前目录是Y1,那么,指定文件F2所需的相对路径是../Y2/F2。如果当前目录是X2,“DEL”表示删除命令,那么,删除文件F4的正确命令是DEL Y3/F4。 -
第3题:
(18)如果一个直线控件在窗体上呈现为一条垂直线,则可以确定的是
A)它的Yl、Y2属性的值相等
B)它的X1、X2属性的值相等
C)它的X1、Yl属性的值分别与X2, Y2属性的值相等
D) 它的X1、X2属性的值分别与Y1、Y2属性的值相等
正确答案:B
-
第4题:
设随机变量X和Y都服从N(0,1)分布,则下列叙述中正确的是:
A.X+Y~N(0,2)
B.X2+Y2~X2分布
C. X2和Y2都~X2分布
D.X2/Y2~F分布答案:C解析:提示:由X2分布定义,X2~X2(1),Y2~X2(1)。X与Y独立时,A、B、D才正确。 -
第5题:
曲面x2+ y2 + z2 = 2z之内以及曲面z = X2 +y2之外所围成的立体的体积V等于: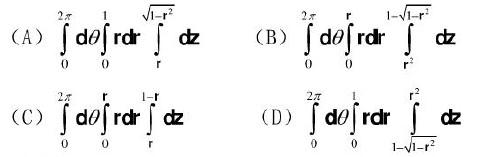 答案:D解析:解:选D.
答案:D解析:解:选D.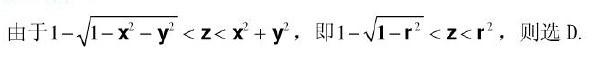
-
第6题:
D 域由 x 轴,x2 + y2 ? 2x = 0( y ≥ 0)及 x+y=2 所围成, f (x, y)是连续函数,化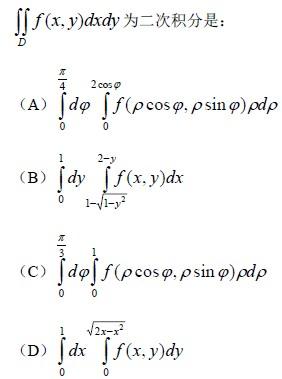 答案:B解析:解:选 B。
答案:B解析:解:选 B。
画积分区域如下图所示,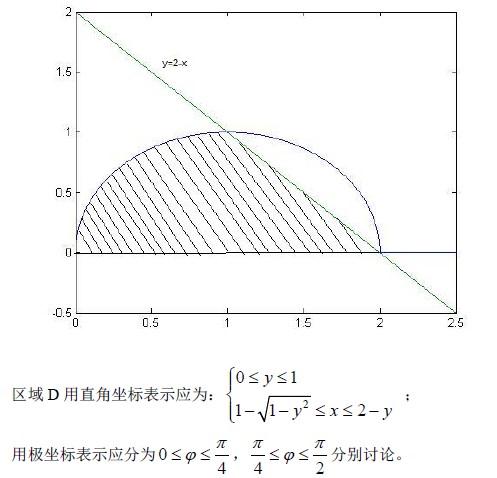
-
第7题:
已知x2=x+1,y2=y+1,且x≠y,则x3+y3=______。答案:解析:4。解析:因为x2=x+1,y2 =y+1且x≠y,所以x,y是方程m2=m+1的两个不同的实数根,所以x+y=1,xy=-1,所以x3+y3=(x+y)(x2-xy+y2)=(x+y)[(x+y)2-3xy]=4。 -
第8题:
设(d/dx)f(x)=g(x),h(x)=x2,则(d/dx)f[h(x)]等于:()
- A、g(x2)
- B、2xg(x)
- C、x2g(x2)
- D、2xg(x2)
正确答案:D -
第9题:
已知X1=+0010100,Y1=+0100001,X2=0010100,Y2=0100001,试计算下列各式(设字长为8位)。 (1)[X1+Y1]补=[X1]补+[Y1]补=() (2)[X1-Y2]补=[X1]补+[-Y2]补=() (3)[X2-Y2]补=[X2]补+[-Y2]补=() (4)[X2+Y2]补=[X2]补+[Y2]补=()
正确答案:00010100+00100001=00110101;00010100+00100001=00110101;11101100+00100001=00001101;11101100+11011111=11001011 -
第10题:
单选题椭园公式为()。A(x2/a2)+(y2/b2)=1
B(x2/a2)-(-y2/b2)=1
C(y2/a2)+(x2/b2)=1
正确答案: C解析: 暂无解析 -
第11题:
单选题使用Line控件在窗体上画一条从(0,0)到(600,700)的直线,则其相应属性的值应是( )。AX1=0,X2=600,Y1=0,Y2=700
BY1=0,Y2=600,X1=0,X2=700
CX1=0,X2=0,Y1=600,Y2=700
DY1=0,Y2=0,X1=600,X2=700
正确答案: A解析:
X1,Y1,X2,Y2属性是直线的起点、终点坐标。 -
第12题:
单选题If ax + x2 = y2 -ay, what is a in terms of x and y?Ay -x
Bx-y
Cx +y
D(x2 + y2)/(x + y)
E(x2 + y2)/(x - y)
正确答案: E解析:
To solve ax + x2 = y2 -ay for a in terms of x and y, isolate a on the left side of the equation: ax+ ay = y2 -x2.
a(x+y)= (x+y)(y –x), a= y –x. -
第13题:
以下程序中,函数fun的功能是计算x2(上标)-2x+6,主函数中将调用fun函数计算:
y1=(x+8)2(上标)-2(x+8)+6
y2=sin2(上标)(x)-2sin(x)+6
请填空。
include "math.h"
double fun(double x){ return (x*x-2*x+6);}
main()
{ double x,y1,y2;
printf("Enter x:"); scanf("%1f",&x);
y1=fim([ ]);
y2=run([ ]);
printf("y1=%1f,y2=%1f\n",y1,y2);
}
正确答案:x+8 sin(x)
x+8 sin(x) 解析:根据函数fun实现的功能可知:主函数中的y1、y2想要实现的是相同的功能,又根据 y1=(x+8)2-2(x+8)+6=(x+8)*(x+8)-2(x+8)+6,可看出y1=fun( [11] );处填:x+8;同理可知y2=fun( [12] );处填sin(x)。 -
第14题:
程序段如下,当发生Form_Click事件时,窗体上输出的结果是( )。 Option Explicit Private x As Integer Public y As Integer Sub Test() Dim y as integer x=2:y=2 Print"x1=";x;"y1=";y End Sub Private Sub Form_Click() x=1:y=1 Test Print "X2=";x;"y2=";y End Sub
A.x1=2 y1=2 x2=2 y2=1
B.x1=2 y1=2 x2=2 y2=2
C.x1=2 y1=1 x2=2 y2=2
D.x1=2 y1=1 x2=2 y2=1
正确答案:A
解析:本题首先定义了一个窗体级变量x和一个全局变量y。当发生窗体的单击事件后,给窗体级变量x和全局变量y分别赋值1,然后调用Test函数。在该函数中定义了一个局部变量y,在函数中使用的y是局部变量,给窗体级变量x赋值2,给局部变量y赋值2,输出的x和y的值都是2。函数调用返回后,窗体级的变量x的值为2,全局变量y的值依旧为1。 -
第15题:
球面x2 + y2 + z2 = 9与平面x + z = 1的交线在xoy坐标面上投影的方程是:
(A) x2 + y2 + (1-x)2 = 9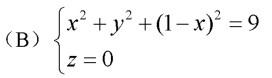
(C) (1-z)2 + y2 + z2 = 9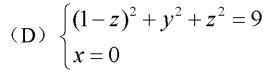 答案:B解析:此题比较简单,注意不要错选(A)。
答案:B解析:此题比较简单,注意不要错选(A)。 -
第16题:
设z=f(x2-y2),则dz 等于:
A. 2x-2y B. 2xdx-2ydy
C. f'(x2-y2)dx D. 2f'(x2-y2)(xdx-ydy)答案:D解析:提示:本题为二元函数求全微分的题目,计算公式为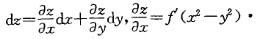
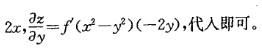
-
第17题:
设f(x)是连续函数,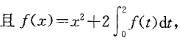 则f(x)=
则f(x)=
A. x2 B. x2-2 C 2x D. x2 -16/9答案:D解析:
-
第18题:
如果从变量y1,y2到x1,x2的线性变换是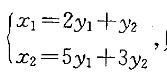 ,则变量x1,x2到变量y1,y2的线性变换是:
,则变量x1,x2到变量y1,y2的线性变换是:
 答案:A解析:
答案:A解析: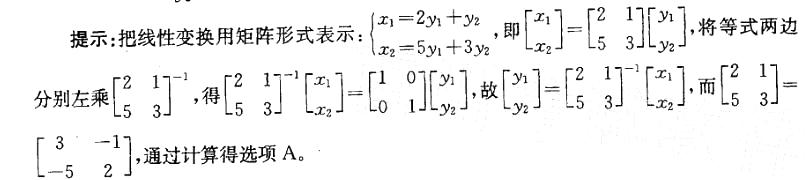
-
第19题:
椭园公式为()。
- A、(x2/a2)+(y2/b2)=1
- B、(x2/a2)-(-y2/b2)=1
- C、(y2/a2)+(x2/b2)=1
正确答案:A -
第20题:
设随机变量X和Y都服从N(0,1)分布,则下列叙述中正确的是()。
- A、X+Y服从正态分布
- B、X2+Y2~x2分布
- C、X2和Y2都服从X2分布
- D、分布
正确答案:C -
第21题:
设随机变量X和Y的相关系数为0.5,E(X)=E(Y)=0,E(X2)=E(Y2)=2,则E(X+Y)2=()。
正确答案:6 -
第22题:
问答题对于两个随机变量X、Y,若E(X2)及E(Y2)都存在,证明:[E(XY)]2≤E(X2)E(Y2)。正确答案:
取f(t)=E[(X+tY)2]=E(X2)+2tE(XY)+t2E(Y2)。所以对任意实数t,E[(X+tY)2]≥0,即f(t)=t2E(Y2)+2tE(XY)+E(X2)≥0。所以Δ=4[E(XY)]2-4E(X2)E(Y2)≤0,故[E(XY)]2≤E(X2)E(Y2)。解析: 暂无解析 -
第23题:
单选题设(d/dx)f(x)=g(x),h(x)=x2,则(d/dx)f[h(x)]等于:()Ag(x2)
B2xg(x)
Cx2g(x2)
D2xg(x2)
正确答案: D解析: 暂无解析
