itgle.com

过点M(3，-2，1)且与平行的直线方程是：

题目
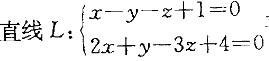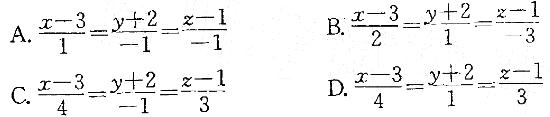
过点M(3，-2，1)且与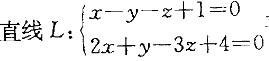平行的直线方程是：

相似考题

1.在y轴上的截距是1，且与x轴平行的直线方程是_______。

2.过点A(1，1，1)与B(2，3，4)的直线方程为( )。

3.已知直线L1过点M1(0，0，-1)且平行于X轴，L2过点M2(0，0，1)且垂直于XOZ平面，则到两直线等距离点的轨迹方程为( )。A. B. C. D.

4.过点（2，1）且与直线y=0垂直的直线方程为 （ ）A.z=2B.x=1C.y=2D.y=1

更多“过点M(3，-2，1)且与平行的直线方程是： ”相关问题

  • 第1题：

    过点（1，－2，3）且平行于z轴的直线的对称式方程是（　　）。



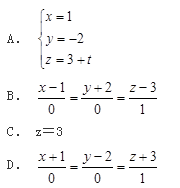    答案：B
    解析：
    由题意可得此直线的方向向量为（0，0，1），又过点（1，－2，3），所以该直线的方程为

  • 第2题：

    已知平面π过点(1，1，0)、(0，0，1)、(0，1，1)，则与平面π垂直且过点(1，1，1)的直线的对称方程为 ( )。



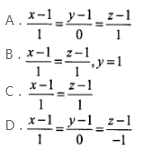    答案：B
    解析：
    平面π的法向量所求直线的方向向量为i+k，故应选B。@##

  • 第3题：

    过点（2，0，－1）且垂直于xOy坐标面的直线方程是（　　）。


    答案：C
    解析：
    垂直于xOy面的直线的方向向量为（0，0，1），由于过点（2，0，－1），则直线的点向式方程为：（x－2）/0＝y/0＝（z＋1）/1。

  • 第4题：

    过(1，2)点且平行于向量a=(2，2)的直线方程为＿＿＿＿＿．


    答案：
    解析：
    【答案】x-y+1=0 【考情点拨】本题主要考查的知识点为直线的斜截式方式．
    【应试指导】设所求直线为L，∵ka=1，L∥a，∴kL=ka=1，又∵L过点(1，2)，∴L的方程为y-2=1×(x-1)，即x-y+1=0．

  • 第5题：

    已知平面π过点M1(1，1，0)，M2(0，0，1)，M3(0，1，1)，则与平面π垂直且过点(1，1，1)的直线的对称方程为：



    答案：A
    解析：
    提示 求出过M1，M2，M3三点平面的法线向量。



    @##

  • 第6题：

    试求通过点Mo(一1，0，4)，垂直于平面Ⅱ：3x一4y-10=0，且与直线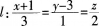
    平行的平面方程。


    答案：
    解析：
    平面Ⅱ的法向量m=（3-4，1)，直线Z的方向向量l=(3，l，2)，所以所求平面的法向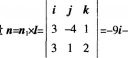

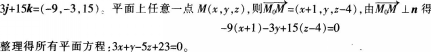
  • 第7题：

    过点Mo(1，-1，0)且与平面x-y+3z=1平行的平面方程为_______.


    答案：
    解析：
    由于已知平面的法线向量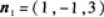所求平面与已知平面平行，可取所求平面法线向量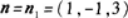又平面过点Mo(1，-1，0)，由平面的点法式方程可知，所求平面为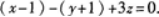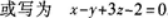【评析】上述两种形式都正确．前者为平面的点法式方程；后者为平面的一般式方程．

  • 第8题：

    已知中心在坐标原点0的椭圆C经过点A(2，3)且点F(2，0)为其右焦点。
    (1)求椭圆C的方程；
    (2)是否存在平行于OA的直线l，使l与椭圆C有公共点，且直线OA与l的距离等于4，若存在，求l方程；若不存在，请证明。


    答案：
    解析：

  • 第9题：

    单选题
    下列判断正确的是（　　）．
    A

    垂直于同一条直线的两条直线互相平行

    B

    过一点有且只有一条直线和已知直线垂直

    C

    过一点有且只有一条直线和一个平面垂直

    D

    过平面外一点，有且只有一条直线和已知平面平行


    正确答案： D
    解析：
    A项，垂直于同一条直线的两条直线可能平行，可能相交，也可能异面；B项，过一点有无数条直线和已知直线垂直；D项，过该点作一平面平行于已知平面，所得平面内过该点的直线都与已知平面平行．

  • 第10题：

    单选题
    过点（2，1）且与直线y＝0垂直的直线方程为（　　）．
    A

    x＝2

    B

    x＝1

    C

    y＝2

    D

    x＝1


    正确答案： D
    解析：
    直线y＝0即为x轴，所求直线要与x轴垂直，即为x＝2．

  • 第11题：

    单选题
    过点（2，1）与直线y＝x垂直的直线方程为（　　）．
    A

    y＝x＋2

    B

    y＝x－1

    C

    y＝－x＋3

    D

    y＝－x＋2


    正确答案： D
    解析：
    与y＝x垂直的直线方程的斜率为－1，设该直线方程为y＝－x＋b，又由于该直线过点（2，1），则1＝－2＋b，得b＝3，则该直线方程为y＝－x＋3．

  • 第12题：

    问答题
    求过点M（－1，0，1）且垂直于直线（x－2）/3＝（y＋1）/（－4）＝z/1又与直线（x＋1）/1＝（y－3）/1＝z/2相交的直线方程。

    正确答案：
    过点M(-1,0,1)且垂直于直线(x-2)/3=(y+1)/(-4)=z/1的平面方程为3x-4y+z+2=0。该平面与直线(x+1)/1=(y-3)/1=z/2的交点为(12,16,26),则该交点与点M(-1,0,1)形成的直线方程为(x+1)/13=y/16=(z-1)/25,即为所求。
    解析： 暂无解析

  • 第13题：

    过点M0(-1，1)且与曲线2ex-2cosy-1 = 0上点(0，π/3)的切线相垂直的直线方程是：


    答案：C
    解析：
    点斜式求出直线方程。

  • 第14题：

    过点M(3，-2，1)且与直线L :平行的直线方程是：


    答案：D
    解析：
    直线L是平面χ - y- z +1 = 0和平面2χ+ y - 3z + 4 = 0的交线，直线L的方向向量

  • 第15题：

    过点P(2，3)且在两条坐标轴上截距相等的直线方程是( )



    答案：D
    解析：
    【考情点拨】本题主要考查的知识点为直线的截距． 【应试指导】如图，

    求在两条坐标轴上截距相等的方程，设截距式方程为

  • 第16题：

    与已知直线7x+24y-5=0平行，且距离等于3的直线方程是。


    答案：
    解析：
    7x+24y+70=0或7x+24y-80=0

  • 第17题：

    a、b是两条异面直线，下列结论正确的是（　　）

    A、过不在a、b上的任一点，可作一个平面与a、b都平行
    B、过不在a、b上的任一点，可作一条直线与a、b都相交
    C、过不在a、b上的任一点，可作一条直线与a、b都平行
    D、过a可以且只可以作一个平面与b平行

    答案：D
    解析：

  • 第18题：

    已知平面π过点(1,1，0)、(0,0,1), (0,1,1),则与平面π垂直且过点(1,1,1)的直线的对称式方程为（ ）。


    答案：B
    解析：
    正确答案是B。
    提示：平面π的法向量，所求直线的方向向量为i+k ,故应选B。

  • 第19题：

    过原点且与平面2x-y+3z+5=0平行的平面方程为______．


    答案：
    解析：
    已知平面的法线向量n1=(2，-1，3)，所求平面与已知平面平行，因此可取所求平面的法线向量n=n1=(2，-1，3)，又平面过原点(0，0，0)，由平面的点法式方程可知，所求平面方程为

  • 第20题：

    在空间直角坐标系中，方程x=2表示（）．

    • A、x轴上的点（2，0，0）
    • B、xOy平面上的直线x=2
    • C、过点（2，0，0）且平行于yOz面的平面
    • D、过点（2，0，0）的任意平面

    正确答案:C

  • 第21题：

    单选题
    在空间直角坐标系中，方程x=2表示（）．
    A

    x轴上的点（2，0，0）

    B

    xOy平面上的直线x=2

    C

    过点（2，0，0）且平行于yOz面的平面

    D

    过点（2，0，0）的任意平面


    正确答案： B
    解析： 暂无解析

  • 第22题：

    单选题
    过点（1，2）且与直线2x＋y－3＝0平行的直线方程为（　　）．
    A

    2x＋y－5＝0

    B

    2y－x－3＝0

    C

    2x＋y－4＝0

    D

    2x－y＝0


    正确答案： B
    解析：
    设和2x＋y－3＝0平行的直线方程为2x＋y＋c＝0，将（1，2）代人，则有2×1＋2＋c＝0，得c＝－4．

  • 第23题：

    单选题
    下列命题中的真命题是（　　）.
    A

    垂直于同一条直线的两条直线平行

    B

    平行于同一条直线的两个平面平行

    C

    过平面外一点有且只有一个平面与该平面垂直

    D

    过平面外一点有且只有一个平面与该平面平行


    正确答案： C
    解析：
    A项，垂直于同一条直线的两条直线平行或相交或异面；B项，平行于同一条直线的两个平面平行或相交；C项，过平面外一点有无数个平面与该平面垂直．

相关内容