itgle.com

设直线的方程为则直线： (A)过点(1,-1,0)，方向向量为2i + j-k (B)过点(1,-1,0)，方向向量为2i - j + k (C)过点(-1,1,0)，方向向量为-2i - j + k (D)过点(-1,1,0)，方向向量为2i + j - k

题目
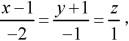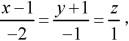设直线的方程为则直线：
(A)过点(1,-1,0)，方向向量为2i + j-k
(B)过点(1,-1,0)，方向向量为2i - j + k
(C)过点(-1,1,0)，方向向量为-2i - j + k
(D)过点(-1,1,0)，方向向量为2i + j - k

相似考题

1.根据下列资料编制直线回归方程 r= 0. 9 a=2.8()A. 直线回归方程yc= 2.8+ 1.08xB.直线回归方程yc= 2.8+ 1.18xC.直线回归方程yc= 0.9+ 1.08xD.直线回归方程yc= 0.9+1.18x

2.对于直线趋势方程Yt=a＋bt,若已知∑t=0,∑tY=130,∑t²=169,a=6,则趋势方程中的b=( )

3.设平面方程为x+y+z+1=0，直线方程为1－x=y+1=z，则直线与平面： A.平行 B.垂直 C.重合 D.相交但不垂直

4.假定被研究现象基本上是按不变的发展速度发展,为描述现象变动的趋势,借以进行预测,应拟合的方程为( )。A. 直线趋势方程B. 指数曲线方程C. 双曲线方程D. 直线或曲线方程均可

更多“设直线的方程为则直线： ”相关问题

  • 第1题：

    设曲线y=y(x)上点P(0，4)处的切线垂直于直线x-2y+5=0，且该点满足微分方程y″+2y′+y=0，则此曲线方程为( )。

    A.
    B.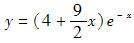
    C.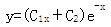
    D.

    答案：D
    解析：

  • 第2题：

    1. 设直线L的方程为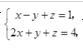

    则L的参数方程是（　　）。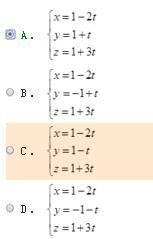


    答案：A
    解析：
    过点M0（x0，y0，z0）的直线，s=（m，n，p）为其一个方向向量，若设参数t如下：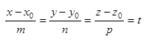

    则其参数式方程可写作

    直线的方向向量应与所在两个平面的法向量都垂直，即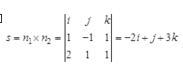

    直线过点（1，1，1），从而参数方程为：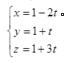

  • 第3题：

    设直线方程为x=y-1=z，平面方程为x-2y+z=0，则直线与平面：
    A.重合 B.平行不重合
    C.垂直相交 D.相交不垂直


    答案：B
    解析：
    从而知直线//平面或直线与平面重合；再在直线上取一点（0,1,0），验证该点是否满足平面方程。

  • 第4题：

    点M（-5,1）关于y轴的对称点M'与点N（1,一1）关于直线l对称,则直线l的方程是（ ）



    答案：C
    解析：

  • 第5题：

    设圆C与圆（x-5）2+y2=2关于直线y=2x对称，则圆C的方程为



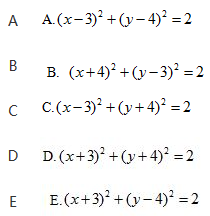    答案：E
    解析：

  • 第6题：


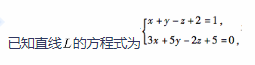
    平面Ⅱ的方程为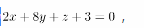

    则直线 与平面Ⅱ的位置关系是( )。


    A.平行
    B.直线在平面内
    C.垂直
    D.相交但不垂直

    答案：A
    解析：
    本题主要考查直线与平面的位置关系的判定。

  • 第7题：

    设直线的方程是Ax+By=0，从1，2，3，4，5这五个数中每次取两个不同的数作为A、B的值，则所得不同直线的条数是（）。

    • A、20
    • B、19
    • C、18
    • D、16

    正确答案:C

  • 第8题：

    在同一平面内，直线与圆弧相切，计算切点坐标的方法是（）。

    • A、将直线方程与圆方程联立求公共解
    • B、将直线方程代入圆方程求解
    • C、将圆方程代入直线方程求解
    • D、将两个方程相加消元求解

    正确答案:A

  • 第9题：

    在直线趋势方程yt=a+bt中，如果b为负值，则这条直线呈（）

    • A、上升趋势
    • B、下降趋势
    • C、不升不降
    • D、无法判定

    正确答案:B

  • 第10题：

    设直线的方程为x=y-1=z，平面的方程为x-2y+z=0，则直线与平面（）。

    • A、重合
    • B、平行不重合
    • C、垂直相交
    • D、相交不垂直

    正确答案:B

  • 第11题：

    单选题
    设直线的方程是Ax+By=0，从1，2，3，4，5这五个数中每次取两个不同的数作为A、B的值，则所得不同直线的条数是（）。
    A

    20

    B

    19

    C

    18

    D

    16


    正确答案： D
    解析： 暂无解析

  • 第12题：

    单选题
    设直线的方程为x=y-1=z，平面的方程为x-2y+z=0,则直线与平面（ ）
    A

    重合

    B

    平行不重合

    C

    垂直相交

    D

    相交不垂直


    正确答案： C
    解析：

  • 第13题：

    设方程y´´-4y´+3y=0的某一积分曲线，它在点(0，2)处与直线x-y+2=0相切，则该积分曲线的方程是( ).

    A.
    B.
    C.
    D.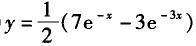

    答案：B
    解析：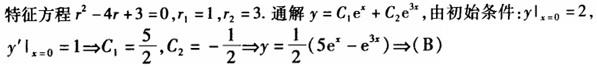

  • 第14题：

    设平面方程x+y+Z+1=0，直线的方程是l-x=y+1= z，则直线与平面：
    (A)平行 （B)垂直 (C)重合 (L)相交但不垂直


    答案：D
    解析：
    解：选D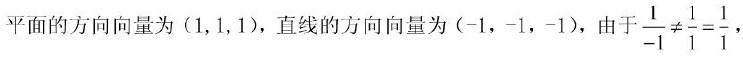
    所以直线与平面不垂直。又1x(-1) + 1x1+1x1=1≠0，所以直线与平面不平行。

  • 第15题：

    设平面方程:x + y + z-1 = 0，直线的方程是1-x = y + 1=z，则直线与平面：
    A.平行 B.垂直 C.重合 D.相交但不垂直


    答案：D
    解析：

  • 第16题：

    以直线y十x=0为对称轴且与直线y-3x=2对称的直线方程为（ ）


    答案：A
    解析：

  • 第17题：

    在平面直角坐标系中，以坐标原点0为极点，x轴的正半轴为极轴建立极坐标系。已知 点A的极坐标为．直线Z的极坐标方程为且点A在直线Z上。
    (1)求。的值及直线Z的直角坐标方程；
    (2)圆C的参数方程为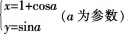试判断直线Z与圆C的位置关系。


    答案：
    解析：
    所以直线l与圆C相交。

  • 第18题：

    设直线的方程为x=y-1=z， 平面的方程为x-2y+z=0，则直线与平面（ ）。
    A.重合 B.平行不重合 C.垂直相交 D.相交不垂直


    答案：B
    解析：
    正确答案为B。
    提示：直线的方向向量为s = (1，1，1)，平面的法向量为n= (1，-2，1)，s·n = 1-2 + 1 = 0,这两个向量垂直，直线与平面平行，又直线上的点(0，1，0)不在平面上，故直线与平面不重合。

  • 第19题：

    已知直线经过（x1，y1）点，斜率为k(k≠0)，则直线方程为y=2kx+2。


    正确答案:错误

  • 第20题：

    某质点的运动方程为x=5+2t-10t2（m），则该质点作（）

    • A、匀加速直线运动，加速度为正值
    • B、匀加速直线运动，加速度为负值
    • C、变加速直线运动，加速度为正值
    • D、变加速直线运动，加速度为负值

    正确答案:B

  • 第21题：

    根据下列资料编制直线回归方程r=0.9a=2.8（）

    • A、直线回归方程yc=2.8+1.08x
    • B、直线回归方程yc=2.8+1.18x
    • C、直线回归方程yc=0.9+1.08x
    • D、直线回归方程yc=0.9+1.18x

    正确答案:A

  • 第22题：

    某质点的运动学方程x=6+3t+5t3，则该质点作（）

    • A、匀加速直线运动，加速度为正值
    • B、匀加速直线运动，加速度为负值
    • C、变加速直线运动，加速度为正值
    • D、变加速直线运动，加速度为负值

    正确答案:C

  • 第23题：

    单选题
    设直线方程为x=y-1=z，平面方程为x-2y+z=0，则直线与平面（　　）。[2011年真题]
    A

    重合

    B

    平行不重合

    C

    垂直相交

    D

    相交不垂直


    正确答案： C
    解析：
    直线的方向向量s＝（1，1，1），平面的法向向量n＝（1，－2，1），其向量积s·n＝1－2＋1＝0，则这两个向量垂直，即直线与平面平行。又该直线上的点（0，1，0）不在平面上，故直线与平面不重合。

相关内容