itgle.com

在多元线性回归模型的基本假定中，随机误差项满足F分布。

题目

在多元线性回归模型的基本假定中，随机误差项满足F分布。

相似考题

1.关于多元线性回归分析应满足的基本假定,以下说法错误的是( )。A.随机误差项服从正态分布B.随机误差项异方差C.随机误差项零均值D.自变量彼此间无多重共线性

2.一元线性回归模型中，随机误差项ε需满足（ ）。

3.应用DW检验方法时应满足该方法的假定条件，下列不是其假定条件的为（ ）A.解释变量为非随机的 B.被解释变量为非随机的 C.线性回归模型中不能含有滞后内生变量 D.随机误差项服从一阶自回归

4.DW检验中要求有假定条件，在下列条件中不正确的是（）A.解释变量为非随机的B.随机误差项为一阶自回归形式C.线性回归模型中不应含有滞后内生变量为解释变量D.线性回归模型只能为一元回归形式

参考答案和解析
解释变量是确定性变量 , 不是随机变量;随机误差项具有 0 均值和等方差 ,;随机误差项相互独立
更多“在多元线性回归模型的基本假定中，随机误差项满足F分布。”相关问题

  • 第1题：

    一元线性回归模型与多元线性回归模型的基本假定是相同的。（ ）


    答案：错
    解析：
    在多元线性回归模型里除了对随机误差项提出假定外，还对解释变量之间提出无多重共线性的假定。

  • 第2题：

    回归分析是期货投资分析中重要的统计分析方法,而线性回归模型是回归分析的基础。线性回归模型的基本假设是（ ）
    Ⅰ.被解释变量与解释变量之间具有线性关系
    Ⅱ.随机误差项服从正态分布
    Ⅲ.各个随机误差项的方差相同
    Ⅳ.各个随机误差项之间不相关

    A：Ⅰ.Ⅱ.Ⅲ.Ⅳ
    B：Ⅰ.Ⅲ.Ⅳ
    C：Ⅰ.Ⅱ.Ⅳ
    D：Ⅱ.Ⅲ.Ⅳ

    答案：A
    解析：
    —元线性回归模型为：yi=a+βi+mi（i=l,2,3,*,n）,其中yi为解解释变量Xi为解释变量;ui是一个随机变垦量.称为随机项。要求随机项u和自变量，Xi满足的统计假定如下：①每个ui均为独立同分右（IID、）,服从正态分右的随机变量，E（ui）=0,V（ui）=σ＾2常数②随机项ui与自变量的任一观察值Xi不相关，即COV（ui,i）=0

  • 第3题：

    回归分析是期货投资分析中重要的统计分析方法，而线性回归模型是回归分析的基础。线性回归模型的基本假设是（ ）。
    I 被解释变量与解释变量之间具有线性关系
    Ⅱ 随机误差项服从正态分布
    Ⅲ 各个随机误差项的方差相同
    Ⅳ 各个随机误差项之间不相关

    A.I、Ⅱ、Ⅲ
    B.I、Ⅲ、Ⅳ
    C.Ⅱ、Ⅲ、Ⅳ
    D.I、Ⅱ、Ⅲ、Ⅳ

    答案：D
    解析：
    一元线性回归模型为：Yi=α+βxi+ui，(i=1，2，3，…，n)，其中Yi为被解释变量，xi为解释变量，ui是一个随机变量，称为随机项。要求随机项ui和自变量xi满足的统计假定如下：①每个ui均为独立同分布，服从正态分布的随机变量，且E(ui)=0， V(ui)=σ2=常数；②随机项ui与自变量的任一观察值xi不相关，即Cov(ui，xi)=0．

  • 第4题：

    根据线性回归模型的基本假定，随机误差项应是随机变量，且满足( )。

    A: 自相关性
    B: 异方差性
    C: 与被解释变量不相关
    D: 与解释变量不相关

    答案：D
    解析：

  • 第5题：

    多元线性回归模型的基本假定有（ ）。

    A.零均值假定
    B.同方差与无自相关假定
    C.异方差假定
    D.无多重共线性假定

    答案：A,B,D
    解析：
    多元线性回归模型满足如下基本假定:（1）零均值假定
    （2）同方差与无自相关假定
    （3）无多重共线性假定，即解释变量之间不存在线性关系。
    （4）随机扰动项与解释变量互不相关
    （5）正态性假定，随机扰动项μi服从正态分布，即μi～N（0，σ2）。
    故C项说法错误。
    考点：多元线性回归模型的基本假定

  • 第6题：

    应用DW检验方法时应满足该方法的假定条件，下列不是其假定条件的为（）

    • A、 解释变量为非随机的
    • B、 被解释变量为非随机的
    • C、 线性回归模型中不能含有滞后内生变量
    • D、 随机误差项服从一阶自回归

    正确答案:B

  • 第7题：

    在线性回归模型中，随机误差μ被假定服从（）

    • A、正态分布
    • B、二项分布
    • C、指数分布
    • D、t分布

    正确答案:A

  • 第8题：

    满足基本假设情况下，应用OLS法估计模型，回归平方和与随机误差项的方差之比ESS/σ2服从（）。

    • A、t分布
    • B、F分布
    • C、χ2分布
    • D、正态分布

    正确答案:C

  • 第9题：

    如果线性回归模型中随机误差项的方差不是（），则称随机误差项具有异方差性。


    正确答案:常数

  • 第10题：

    在人力资源预测中，最常用的模型是（）

    • A、线性回归预测模型
    • B、时间序列预测模型
    • C、一元线性回归预测模型
    • D、多元线性回归模型

    正确答案:A

  • 第11题：

    在构建回归模型时，应当对模型进行检验，下列哪些论述是正确的（）。

    • A、在一元线性回归分析中，只进行回归系数b的t检验是足够的
    • B、在一元线性回归分析中，应当同时进行回归系数b的t检验和模型整体的F检验
    • C、在多元回归分析中，回归系数b的t检验和模型整体的F检验是等价的
    • D、在多元回归分析中，回归系数b的t检验和模型整体的F检验是不等价的

    正确答案:A,D

  • 第12题：

    问答题
    多元线性回归模型中有哪些基本的假定？

    正确答案：
    多元回归模型的基本假定有:
    (1)随机误差项εi具有零均值和同方差,即:E(εi)=0,D(εi)=σ2;
    (2)随机误差项在不同样本点之间是相互独立的,不存在序列关系,即: Cov(εi,εj)=0,(i≠j);
    (3)随机误差项εi应服从正态分布,即:εi~N(0,σ2);
    (4)自变量x1,x2,…,xp是确定性变量,且它们之间是不相关的;
    (5)因变量与自变量x1,x2,…,xp之间存在着显著的线性相关关系,即模型是线性的。
    解析： 暂无解析

  • 第13题：

    回归分析是期货投资分析中重要的统计分析方法，而线性回归模型是回归分析的基础。线性回归模型中关于随机项μi的基本假设是（ ）。
    Ⅰ.随机项μi自变量的任一观察值xi不相关
    Ⅱ.E（μi）=0，V（μi）=σμ^2=常数
    Ⅲ.线每个μi为独立同分布，服从正态分布的随机变量
    Ⅳ.各个随机误差项之间不相关

    A.Ⅰ.Ⅱ.Ⅲ
    B.Ⅰ.Ⅱ.Ⅲ.Ⅳ
    C.Ⅱ.Ⅲ.Ⅳ
    D.Ⅰ.Ⅲ.Ⅳ

    答案：B
    解析：
    一元线性回归模型为：yi=α十βxi+μi，（i=1，2，3，....），其中yi为被解释变量；xi为解释变量；μi是一个随机变量，称为随机项。随机项μi满足如下基本假定：①每个μi均为独立同分布，服从正态分布的随机变量，且E（μi）=0，V（μi）=σμ∧2=常数；②每个随机项μi均互不相关，即：Cov（μi，μj）=0 （i≠j）；③随机项μi与自变量的任一观察值xi不相关，即：Cov（μi，xi）=0 （i=1，2，3，...，n）。

  • 第14题：

    回归分析是期货投资分析中重要的统计分析方法，而线性回归模型早回归分析的基础。线性回归模型中关于随机项μi的基本假设是（ ）。
    Ⅰ.随机项μi与自变量的任一观察值xi不相关=常数
    Ⅱ.
    Ⅲ.每个μi均为独立同分布，服从正态分布的随机变量
    Ⅳ.各个随机误差项之间不相关

    A、Ⅰ.Ⅱ.Ⅲ.Ⅳ
    B、Ⅰ.Ⅱ.Ⅲ
    C、Ⅰ.Ⅱ.Ⅳ
    D、Ⅱ.Ⅲ.Ⅳ


    答案：A
    解析：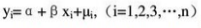
    一元线性回归模型为:，其中yi为被解释变量；xi为解释变量；μi是一个随机变量，称为随机项。随机项μi满足如下基本假定:①每个μi均为独立同分布，服从正态分布的随机变量，且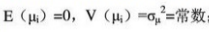；②每个随机相Ri均互不相关，即；③随机项Ri与自变量的任一观察值xi不相关,即: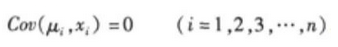


  • 第15题：

    回归分析是期货投资分析中重要的统计分析方法，而线性回归模型是回归分析的基础。线性回归模型中关于随机项i的基本假设是（ ）。
    Ⅰ.随机项i与自变量的任一观察值Xi不相关
    Ⅱ. E(i)=0,V(i)=σ2=常数
    Ⅲ.每个i均为独立同分布，服从正态分布的随机变量
    Ⅳ.各个随机误差项之间不相关

    A、Ⅰ.Ⅱ.Ⅲ
    B、Ⅰ.Ⅱ.Ⅲ.Ⅳ
    C、Ⅱ.Ⅲ.Ⅳ
    D、Ⅰ.Ⅱ.Ⅳ


    答案：B
    解析：

  • 第16题：

    根据线性回归模型的基本假定，随机误差项应是随机变量，且满足()。

    A.自相关性
    B.异方差性
    C.与被解释变量不相关
    D.与解释变量不相关

    答案：D
    解析：

  • 第17题：

    多元线性回归模型随机干扰项的假定有哪些？


    正确答案: （1）随机误差项的条件期望值为零。
    （2）随机误差项的条件方差相同。
    （3）随机误差项之间无序列相关。
    （4）自变量与随机误差项独立无关。
    （5）随机误差项服从正态分布。
    （6）各解释变量之间不存在显著的线性相关关系。

  • 第18题：

    使用普通最小二乘法在对自回归模型进行估计时，若随机误差项满足经典线性回归模型的所有假定，则估计量是一致估计量的模型是（）

    • A、Koyck变换模型
    • B、部分调整模型
    • C、自适应预期模型
    • D、自适应预期和部分调整混合模型

    正确答案:B

  • 第19题：

    在线性回归模型中，假定随机误差ε（）。

    • A、同方差
    • B、异方差
    • C、独立性
    • D、数学期望为0
    • E、服从正态分布

    正确答案:A,C,D,E

  • 第20题：

    DW检验中要求有假定条件，在下列条件中不正确的是（）

    • A、解释变量为非随机的
    • B、随机误差项为一阶自回归形式
    • C、线性回归模型中不应含有滞后内生变量为解释变量
    • D、线性回归模型只能为一元回归形式

    正确答案:D

  • 第21题：

    多重线性回归模型的基本假定有哪些？如何判断资料是否满足这些假定？如果资料不满足假定条件，常用的处理方法有哪些？


    正确答案:多重线性回归的前提条件是线性、独立性、正态性和等方差性，可以借助残差分析等方法判断资料是否满足条件。如果资料不满足前提条件，可以采用变量变换和非线性回归等方法处理。

  • 第22题：

    在一元线性回归分析中，通常假定随机误差项e满足（）。

    • A、E（e）=0
    • B、E（e）1=0
    • C、Var（e）=s2
    • D、Var（e）=1

    正确答案:A,C

  • 第23题：

    单选题
    回归分析是期货投资分析中重要的统计分析方法，而线性回归模型是回归分析的基础。线性回归模型的基本假设是（　　）。Ⅰ．被解释变量与解释变量之间具有线性关系Ⅱ．随机误差项服从正态分布Ⅲ．各个随机误差项的方差相同Ⅳ．各个随机误差项之间不相关
    A

    Ⅰ、Ⅱ、Ⅲ

    B

    Ⅰ、Ⅲ、Ⅳ

    C

    Ⅱ、Ⅲ、Ⅳ

    D

    Ⅰ、Ⅱ、Ⅲ、Ⅳ


    正确答案： A
    解析：
    一元线性回归模型为：yi＝α＋βxi＋ui（i＝1，2，3，…，n），其中yi为被解释变量；xi为解释变量；ui是一个随机变量，称为随机项。要求随机项ui和自变量xi满足的统计假定如下：①每个ui均为独立同分布，服从正态分布的随机变量，且E（ui）＝0，V（ui）＝σ2＝常数；②随机项ui与自变量的任一观察值xi不相关，即Cov（ui，xi）＝0。

  • 第24题：

    问答题
    多元线性回归方程有哪些基本假定？在实际应用中，若这些假定并不满足，会造成怎样的不良后果？

    正确答案： 多元线性回归模型的基本假定有：零均值假定、随机项独立同方差假定、解释变量的非随机性假定、解释变量之间不存在线性相关关系假定、随机误差项μi服从均值为0方差为σ2的正态分布假定。在证明最小二乘估计量的无偏性中，利用了解释变量与随机误差项不相关的假定；在有效性的证明中，利用了随机项独立同方差假定。
    若这些假定不满足，会遇到较多问题，主要有多重共线性问题以及自相关、异方差等问题。
    解析： 暂无解析

相关内容