为了了解某企业职工的平均工资收入情况,按重复抽样方法随机抽取了50名职工进行调查,调查结果如下:样本月平均收入2200元,按修正方差公式计算的样本标准差为640元。若其他条件不变,若以95.45%的概率保证程度,要使估计的最大误差控制在100元以内,则至少要抽取____________个样本单位。
题目
为了了解某企业职工的平均工资收入情况,按重复抽样方法随机抽取了50名职工进行调查,调查结果如下:样本月平均收入2200元,按修正方差公式计算的样本标准差为640元。若其他条件不变,若以95.45%的概率保证程度,要使估计的最大误差控制在100元以内,则至少要抽取____________个样本单位。
相似考题
参考答案和解析
更多“为了了解某企业职工的平均工资收入情况,按重复抽样方法随机抽取了50名职工进行调查,调查结果如下:样本月平均收入2200元,按修正方差公式计算的样本标准差为640元。若其他条件不变,若以95.45%的概率保证程度,要使估计的最大误差控制在100元以内,则至少要抽取____________个样本单位。”相关问题
-
第1题:
某地区居民户数为10000户,其平均月消费水平标准差为100元。采取简单随机重复抽样抽取样本进行调查,以了解其月平均消费水平,若可靠程为95.45%,误差不超过10元,则应抽取()户居民进行调查。参考答案:100
-
第2题:
用简单随机抽样(重复抽样)方法抽取样本单位,如果要使抽样平均误差降低50%,则样本容量需扩大到原来的()。
A、2倍
B、3倍
C、4倍
D、5倍
参考答案:C
-
第3题:
用简单随机重复抽样方法抽取样本单位,如果要使抽样平均误差降低50%,则样本容量需要扩大到原来的( )倍。
 正确答案:C
正确答案:C
-
第4题:
为了解学生上网情况,从某高校随机抽取了100名学生进行调查。调查结果显示,有38名学生每天上网的时间超过了4个小时。则样本比例的方差为( )。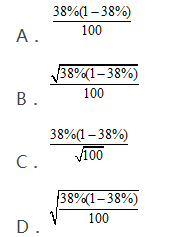 答案:A解析:
答案:A解析: -
第5题:
某工厂有1500个工人,用简单随机重复抽样的方法抽出50个工人作为样本,调查其月平均产量水平,资料如下:
 以95.45%的可靠性估计该厂工人的月平均产量和总产量的区间。
以95.45%的可靠性估计该厂工人的月平均产量和总产量的区间。
略 -
第6题:
用简单随机重复抽样方法抽取样本的单位,如果要使抽样平均误差降低50%,则样本容量需要扩大到原来的()
- A、2倍
- B、3倍
- C、4倍
- D、5倍
正确答案:C -
第7题:
抽样方法按抽取样本的方法不同,可分为()
- A、大样本和小样本
- B、重复抽样和不重复抽样
- C、点估计和区间估计
- D、纯随机抽样和分层抽样
正确答案:B -
第8题:
抽样判断的特点是()
- A、由推算认识总体的一种方法
- B、按随机原则抽取样本单位
- C、运用概率估计的方法
- D、可以计算,但不能控制抽样误差
- E、可以计算并控制抽样误差
正确答案:A,B,C,E -
第9题:
参数估计的特点是()
- A、由推算认识总体的一种方法
- B、按随机原则抽取样本单位
- C、运用概率估计的方法
- D、可以计算,但不能控制抽样误差
- E、可以计算并控制抽样误差
正确答案:A,B,C,E -
第10题:
在简单随机重复抽样条件下,当概率保证程度从68.27%提高到95.45%时,若其他条件不变,则必要的样本容量应该()
- A、增加1倍
- B、增加2倍
- C、增加3倍
- D、减少2倍
正确答案:C -
第11题:
在其他条件不变的情况下,扩大样本容量可以()。
- A、降低总体方差
- B、降低抽样误差
- C、提高估计的精确性
- D、提高区间估计的概率保证程度
正确答案:B,C,D -
第12题:
多选题在其他条件不变的情况下,扩大样本容量可以()。A降低总体方差
B降低抽样误差
C提高估计的精确性
D提高区间估计的概率保证程度
正确答案: D,B解析: 暂无解析 -
第13题:
某地区居民户数为10000户,其平均月消费水平标准差为100元。采取简单随机重复抽样抽取样本进行调查,以了解其月平均消费水平,若可靠程序为95.45%,误差不超过10元,则应抽取()户居民进行调查。A、100户
B、200户
C、400户
D、1000户
参考答案:A
-
第14题:
用简单随机重复抽样方法抽取样本单位,如果要使抽样平均误差降低50%,则样本容量需要扩大到原来的()。A、2倍
B、3倍
C、4倍
D、5倍
标准答案:C
-
第15题:
某地有2万亩稻田,根据上年资料得知其中平均亩产的标准差为50公斤,若以95.45%的概率保证平均亩产的误差不超过10公斤,按重复抽样条件计算,应抽选( )亩地作为样本进行抽样调查。
A.100
B.250
C.500
D.1000
正确答案:A
解析:
-
第16题:
从某年级学生中按简单随机抽样方式抽取40名学生,对统计学原理课的考试成绩进行检查,得知其平均分数为78.75分,样本标准差为12.13分,试以95.45%的概率保证程度推断全年级学生考试成绩的区间范围。如果其它条件不变,将允许误差缩小一半,应抽取多少名学生?

略 -
第17题:
在某乡2万亩水稻中按重复抽样方法抽取400亩,得知平均亩产量为609斤,样本标准差为80斤。要求以95.45%【z=2】概率保证程度估计该乡水稻的平均亩产量和总产量的区间范围。

略 -
第18题:
对某厂日产10000个灯泡的使用寿命进行抽样调查,抽取100个灯泡,测得其平均寿命为1800小时,标准差为6小时。要求: (1)按68.27%概率计算抽样平均数的极限误差; (2)按以上条件,若极限误差不超过0.4小时,应抽取多少只灯泡进行测试; (3)按以上条件,若概率提高到95.45%,应抽取多少灯泡进行测试? (4)若极限误差为0.6小时,概率为95.45%,应抽取多少灯泡进行测试? (5)通过以上计算,说明极限误差、抽样单位数和概率之间的关系。
正确答案: (1)极限误差为0.6小时
(2)应抽取225只灯泡进行测试
(3)应抽取900只灯泡进行测试
(4)应抽取400只灯泡进行测试
(5)极限误差大小、抽样单位数的多少和概率保证程度成正比关系。 -
第19题:
用简单随机重复抽样抽取样本*单位,如果要使抽样平均误差降低50%,则样本容量要扩大到原来的()
- A、2倍
- B、3倍
- C、4倍
- D、5倍
正确答案:C -
第20题:
抽样推断的特点有()
- A、由部分认识总体的一种方法
- B、按随机原则抽取样本*单位
- C、运用概率估计的方法
- D、可以消除抽样误差
- E、可以计算并控制抽样误差
正确答案:A,B,C,E -
第21题:
在重复简单随机抽样条件下,抽样平均误差与总体标志变动度的大小成(),与样本容量的平方根成()。如其他条件不变,要使抽样平均误差减少,则样本容量应()。
正确答案:正比;反比;增加 -
第22题:
简单重复抽样条件下,若概率保证程度从68.27%增大到95.45%,则所需样本容量也将增大2倍。
正确答案:错误 -
第23题:
多选题参数估计的特点是()A由推算认识总体的一种方法
B按随机原则抽取样本单位
C运用概率估计的方法
D可以计算,但不能控制抽样误差
E可以计算并控制抽样误差
正确答案: D,E解析: 暂无解析 -
第24题:
多选题抽样判断的特点是()A由推算认识总体的一种方法
B按随机原则抽取样本单位
C运用概率估计的方法
D可以计算,但不能控制抽样误差
E可以计算并控制抽样误差
正确答案: B,A解析: 暂无解析

 以95.45%的可靠性估计该厂工人的月平均产量和总产量的区间。
以95.45%的可靠性估计该厂工人的月平均产量和总产量的区间。

