itgle.com

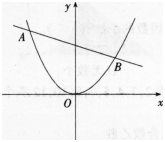
如图所示，已知A，B为直线L：y=mx-m+2与抛物线y=x2的两个交点。 (1)直线ι经过一个定点C，试求出点C的坐标；(2分) (2)若m=-1，已知在直线L下方的抛物线上存在一点P(点P与坐标原点0不重合)，且△ABP的面积为（3√13）/2，求点P的坐标。(6分)

题目
如图所示，已知A，B为直线L：y=mx-m+2与抛物线y=x2的两个交点。
(1)直线ι经过一个定点C，试求出点C的坐标；(2分)
(2)若m=-1，已知在直线L下方的抛物线上存在一点P(点P与坐标原点0不重合)，且△ABP的面积为（3√13）/2，求点P的坐标。(6分)

相似考题

1.已知抛物线y=ax2-1的焦点是坐标原点，则以抛物线与两坐标轴的三个交点为顶点的三角形面积为_______。

2.已知n=5，∑x=15，∑x2=55，∑xy=506，∑y=158，∑y2=5100， (1)计算相关系数； (2)建立直线回归方程。

3.在抛物线y＝x2(第一象限部分，且2≤8)上求一点，使过该点的切线与直线y＝0，x＝8相交所围成的三角形的面积为最大．

4.已知曲线C为y= 2x2，直线l为y= 4x．（10分）(1)求由曲线C与直线l所围成的平面图形的面积S；(2)求过曲线C且平行于直线l的切线方程．

更多“如图所示，已知A，B为直线L：y=mx-m+2与抛物线y=x2的两个交点。 ”相关问题

  • 第1题：

    分别写出抛物线y=4x2与y=-x2/4的开口方向、对称轴及顶点。


    1.y=4x2

    ∵a=4>0 ∴开口向上

    又∵b=c=0, ∴顶点在原点，对称轴为y轴

    2. y=-x2/4

    ∵a=-1/4<0 ∴开口向下

    又∵b=c=0, ∴顶点在原点，对称轴为y轴


  • 第2题：

    直线回归方程y=a+bx ，式中b表示回归直线与y轴的交点到原点的距离。

    此题为判断题(对，错)。


    正确答案：×

  • 第3题：

    设L为连接(0,0)点与(1,1)点的抛物线y =x2 ，则对弧长的曲线积分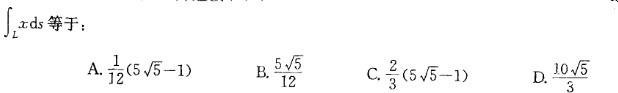


    答案：A
    解析：
    提示:利用对弧长的曲线积分方法计算。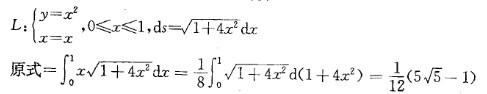

  • 第4题：

    设曲线y=^e1?x2与直线x=-1的交点为P，则曲线在点P处的切线方程是（　　）

    A．2x-y+2=0
    B．2x+y+1=0
    C．2x+y-3=0
    D．2x-y+3=0

    答案：D
    解析：


    @##

  • 第5题：

    已知双曲线C：x2/a2-y2/b2=1(a>0，b>0)的一个焦点是抛物线y2=8x的焦点，且双曲线C的离心率为2，那么双曲线C的方程为_______。


    答案：
    解析：

  • 第6题：

    过直线3x＋2y＋1＝0与2x－3y＋5＝0的交点，且垂直于直线L：6x－2y＋5＝0的直线方程是（　　）

    A.x－3y－2＝0
    B.x＋3y－2＝0
    C.x－3y＋2＝0
    D.x＋3y＋2＝0

    答案：B
    解析：

  • 第7题：

    已知直线在x轴上的截距为-1，在y轴上的截距为1，又抛物线y=x2+bx+c的顶点坐标为(2，-8)，求直线和抛物线两个交点横坐标的平方和．


    答案：
    解析：

    设直线与抛物线两交点的横坐标为x1和x2，则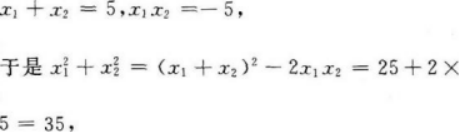

    即直线与抛物线两交点的横坐标的平方和为35．

  • 第8题：

    直线y=ax+b与抛物线y=x2有两个交点。（1）a2>4b。（2）b>0。

    A.条件（1）充分，但条件（2）不充分
    B.条件（2）充分，但条件（1）不充分
    C.条件（1）和（2）都不充分，但联合起来充分
    D.条件（1）充分，条件（2）也充分
    E.条件（1）不充分，条件（2）也不充分，联合起来仍不充分

    答案：B
    解析：
    代数解法，联立两个方程得x2=ax+b，x2-ax-b=0若有两个交点，则▲＝a2+4b>0，可知条件（1）不充分，条件（2）充分。此题选B

  • 第9题：

    已知抛物线y2=2px(p>0)，过定点(p，0)作两条互相垂直的直线l1、l2，l1与抛物线交于


    答案：
    解析：
    (pk2+P，-pk)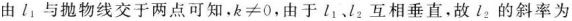

  • 第10题：

    由抛物线y=x2与三直线x=a，x=a+1，y=0围成平面图形。问a为何值时图形的面积最小？（）

    • A、1
    • B、-1／2
    • C、0
    • D、2

    正确答案:B

  • 第11题：

    单选题
    若方程Y=a+bX中的截距a<0，说明（）
    A

    随着X的增大，y增大

    B

    随着X的增大，y减少

    C

    随着X的减少，y减少

    D

    回归直线与y轴的交点在原点下方

    E

    回归直线与y轴的交点在原点上方


    正确答案： A
    解析： 暂无解析

  • 第12题：

    单选题
    直线y＝3x－3与抛物线y＝x2－x＋1的交点有（　　）．
    A

    0个

    B

    1个

    C

    2个

    D

    无法确定


    正确答案： B
    解析：
    令x2－x＋1＝3x－3，整理得x2－4x＋4＝0，解之得x＝2．只有一解，说明直线y＝3x－3与抛物线y＝x2－x＋1只有一个交点．

  • 第13题：

    （2）抛物线y=ax²+bx+c与x轴的两交点的横坐标分别是-1/2,3/2,与y轴交点的纵坐标是-5。


    解：设y=a(x-x1)(x-x2) =a(x+1/2)(x-3/2) 与y轴的交点的纵坐标是-5 所以y=20(x+1/2)(x-3/2)/3 化简得y=20x2/3-20x/3-5

  • 第14题：

    若方程Y=a＋bX中的截距a<0，说明A、随着X的增大，Y增大B、随着X的增大，Y减少C、随着X的减少，Y减少D、回

    若方程Y=a+bX中的截距a<0，说明

    A、随着X的增大，Y增大

    B、随着X的增大，Y减少

    C、随着X的减少，Y减少

    D、回归直线与Y轴的交点在原点下方

    E、回归直线与Y轴的交点在原点上方


    参考答案：B

  • 第15题：

    由抛物线y=x2与三直线x=a，x=a+1，y=0所围成的平面图形，a为下列（　　）值时图形的面积最小。


    答案：B
    解析：
    平面图形的面积

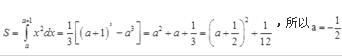
    时图形面积最小。

  • 第16题：

    已知曲线C为y=2x2及直线L为y=4x．
    ①求由曲线C与直线L所围成的平面图形的面积S；
    ②求曲线C的平行于直线L的切线方程．


    答案：
    解析：
    画出平面图形如图l一3—4阴影所示．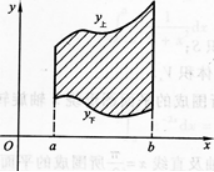
    图1—3—3

    图1—3—4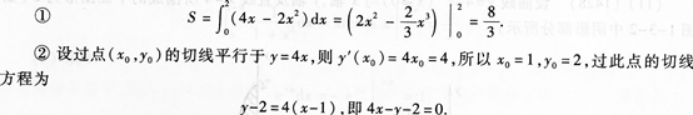

  • 第17题：

    已知x2=x+1，y2=y+1，且x≠y，则x3+y3=______。


    答案：
    解析：
    4。解析：因为x2=x+1，y2 =y+1且x≠y，所以x，y是方程m2=m+1的两个不同的实数根，所以x+y=1，xy=-1，所以x3+y3=(x+y)(x2-xy+y2)=(x+y)[(x+y)2-3xy]=4。

  • 第18题：

    曲线y=x2+1与直线y=2x的交点坐标为()


    答案：A
    解析：

  • 第19题：

    直线l1与直线l2：3x+2y-12=0的交点在x轴上，且l1⊥l2，则l1在y轴上的截距是（）



    答案：B
    解析：

  • 第20题：

    χ2+χy+y2=l表示的曲线是( )。

    A、椭圆
    B、双曲线
    C、抛物线
    D、两条相交直线

    答案：A
    解析：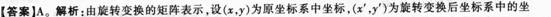

  • 第21题：

    粘度法实验中，当用外推法做图求[η]值时，如ηsp/C、lnηr/C与y轴三条直线不能相交于一点时，应该用哪两条直线交点作为[η]值较为准确（）。

    • A、ηsp/C与lnηr/C的交点
    • B、ηsp/C与y轴的交点
    • C、lnηr/C与y轴的交点

    正确答案:B

  • 第22题：

    若方程Y=a+bX中的截距a<0，说明（）

    • A、随着X的增大，y增大
    • B、随着X的增大，y减少
    • C、随着X的减少，y减少
    • D、回归直线与y轴的交点在原点下方
    • E、回归直线与y轴的交点在原点上方

    正确答案:D

  • 第23题：

    单选题
    由抛物线y=x2与三直线x=a，x=a+1，y=0围成平面图形。问a为何值时图形的面积最小？（）
    A

    1

    B

    -1／2

    C

    0

    D

    2


    正确答案： D
    解析： 暂无解析

相关内容