itgle.com

12个同类产品中，有10个正品，任意抽取3个产品的概率为1的事件是（）。A．3个都是正品B．至少有一个是次品C．3个都是次品D．至少有一个是正品

题目

12个同类产品中，有10个正品，任意抽取3个产品的概率为1的事件是（）。

A．3个都是正品

B．至少有一个是次品

C．3个都是次品

D．至少有一个是正品

相似考题

1.一批产品包括10件正品,3件次品(1)不放回地抽取,每次一件,直到取得正品为止,假定每件产品被取到的机会相同,求抽取次数的概率分布列。(2)每次取出一件产品后,总以一件正品放回去,直到取得正品为止,求抽取次数的概率分布列。

2.甲箱中有5个正品，3个次品；乙箱中有4个正品，3个次品。从甲箱中任取3个产品放入乙箱，然后从乙箱中任取1个产品，则这个产品是正品的概率为( )。A．0.176B．0.2679C．0.3342D．0.5875

3.事件A为“随机抽取3件产品，且至少有一件是正品”，事件B为“随机抽取3件产品，且有两件正品一件次品”，那么( )。A．事件A与事件B互不相容B．事件A与事件B互相独立C．事件A与事件B互相对立D．事件A包含事件B

4.一箱产品中有a件正品和b件次品,若随机地将产品一个接一个的摸取出来,(1)不放回抽取;(2)有放回抽取。求第k次摸到的是正品的概率。

参考答案和解析
至少有一个是正品
更多“12个同类产品中，有10个正品，任意抽取3个产品的概率为1的事件是（）。”相关问题

  • 第1题：

    10个产品中有7个正品,3个次品,按不放回抽样,抽取2个产品,求两次都取到次品的概率是

    A.2/15

    B.3/10

    C.2/9

    D.1/15


    参考答案:D

  • 第2题：

    在一个制造过程中，其产品的不合格品率为0.03，随机抽取9件产品，其中恰有1件不合格品的概率为（ ）。

    A.0.2116

    B.0.4796

    C.0.5204

    D.0.8489


    正确答案：A
    A。

  • 第3题：

    从一批有10件正品及2件次品的产品中，不放回地一件一件地抽取产品，设每个产品被抽到的可能性相同，求直到取出正品为止所需抽取的次数X的概率分布。


    答案：
    解析：
    由题意，x的所有可能的取值为1，2，3，

  • 第4题：

    从一批产品中任意抽取10件，检验其中不合格品的数目，事件A= “不合格品恰为3件”与事件B= “不合格品少于5件”的关系为（ ）。


    答案：A
    解析：
    。不合格品为3件，一定少于5件。

  • 第5题：

    10件产品中4件为次品,6件为正品,现抽取2件产品.
    　　(1)求第一件为正品,第二件为次品的概率；
    　　(2)在第一件为正品的情况下,求第二件为次品的概率；
    　　(3)逐个抽取,求第二件为正品的概率.


    答案：
    解析：
    (1)令Ai={第i次取到正品}（i=1，2），则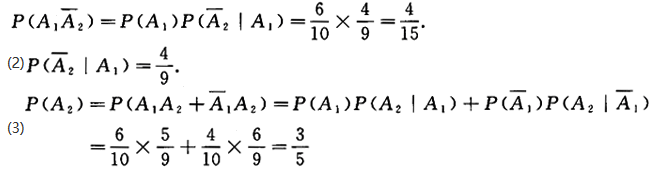

  • 第6题：

    关于事件A的概率，叙述正确的有（ ）。

    A：由于频率总介于0与1之间，故随机事件A的概率也总是介于0与1之间
    B：若A为必然事件，则其概率是1
    C：若A为不可能事件，则其概率是0
    D：若事件A在10次试验中发生10次，则事件A的概率为1
    E：若A为小概率事件，通常认为在一次试验中A几乎不可能发生

    答案：A,B,C,E
    解析：

  • 第7题：

    一批产品共有十个正品和2个次品。任意抽取两次，每次抽取一个后不再放回。则第二次抽取的是次品的概率是（）。

    • A、1/5
    • B、六分之一
    • C、十一分之一
    • D、十二分之一

    正确答案:B

  • 第8题：

    概率的基本性质有（）。

    • A、概率是非负的，其数值介于0与1之间，即对任意事件A有0≤P(A)≤1
    • B、P()+P(A)＝1
    • C、P(AB)＝P(A)P(B)
    • D、必然事件的概率为1

    正确答案:A,B,D

  • 第9题：

    如果100件产品中，有10件次品，不放回地从中接连抽取两次，每次抽取一件，则第二次取到次品的概率是1/10


    正确答案:正确

  • 第10题：

    两个事件A和B互斥，且概率都不为0.如果已知事件A发生，此时事件B发生的概率为（）。

    • A、1
    • B、任意正值
    • C、0
    • D、0到1之间的任意值

    正确答案:C

  • 第11题：

    多选题
    概率的基本性质有（）。
    A

    概率是非负的，其数值介于0与1之间，即对任意事件A有0≤P(A)≤1

    B

    P()+P(A)＝1

    C

    P(AB)＝P(A)P(B)

    D

    必然事件的概率为1


    正确答案： A,B
    解析： 注意性质的条件。C中应有A与B相互独立的条件。

  • 第12题：

    单选题
    假设一批产品有100件产品，批不合格率p=10%，从中任意抽取2件产品，不合格抽取概率P（0）为（）。
    A

    0.75

    B

    0.81

    C

    0.90

    D

    0.50


    正确答案： C
    解析： 暂无解析

  • 第13题：

    在n重贝努里试验中,若事件A在每次试验中发生的概率为p,试证明:对任意ε>0,事件A发生的频率A与事

    在n重贝努里试验中,若事件A在每次试验中发生的概率为p,试证明:对任意ε>0,事件A发生的频率A与事件un/n发生的概率p有如下关系:

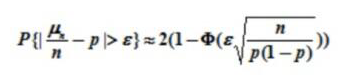
    请帮忙给出正确答案和分析，谢谢!


    答案：

    解析：二项分布的期望为np，方差为np(1-p)，该题将二项分布近似正态分布来求解。

  • 第14题：

    有10件产品，其中8件是正品，2件是次品．甲、乙两人先后各抽取1件产品，
    求甲先抽到正品的条件下，乙抽到正品的概率．


    答案：
    解析：
    这是求在甲事件发生的条件下，乙事件发生的概率，故是条件概率．设A={甲抽到正品}，B={乙抽到正品}，所求为P(B|A)．
    解法l在缩小的样本空间中求条件概率，此时样本空间的样本点为9件产品中有7件正品，2件次品，所以


  • 第15题：

    设盒中有10个灯泡，其中次品3个，每次不放回地任取1个且任取两次．求
    (1)第二次取到的也是正品的概率；(2)两次取到的都是正品的概率；
    (3)第二次取到的是正品的概率．


    答案：
    解析：

  • 第16题：

    甲箱中有5个正品，3个次品；乙箱中有4个正品，3个次品。从甲箱中任取3个产品放入乙箱，然后从乙箱中任取1个产品，则这个产品是正品的概率为（ ）。
    A. 0. 176 B. 0. 2679 C. 0. 3342 D. 0. 5875


    答案：D
    解析：
    设B={从乙箱中取得正品}，A1={从甲箱中取出3个正品}，A2={从甲箱中取出2个正品1个次品}，A3={从甲箱中取出1个正品2个次品}，A4 ={从甲箱中取出3 个次品}，显然A1、A2、A3、A4都是互斥的，所以B=B(A1 + A2+ A3+ A4)。


    P(B A1) =7/10，P(B A2) =6/10，P(B A3) =5/10，P(B A4) =4/10；
    故P(B) =P(BA1+BA2 + BA3+ BA4) =P(A1)P(B A1) +P(A2)P(B A2) +P(A3)P (B A3) +P(A4)P(B A4) = (10/56) x (7/10) + (30/56) x (6/10) + (15/56) x (5/ 10) + (1/56) x (4/10) =0.5875。

  • 第17题：

    一批产品有10个正品2个次品,任意抽取两次,每次取一个,抽取后不放回,求第二次抽取次品的概率.


    答案：
    解析：
    【解】令A1={第一次抽取正品}，A2={第一次抽取次品}，B={第二次抽取次品}，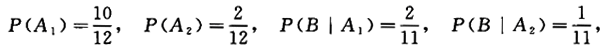

    由全概率公式得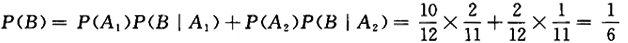

    注解 不放回抽取的情况下，第一次抽取的结果未知时，第二次抽取某种产品的概率与第一次抽取的概率相同。

  • 第18题：

    从10个编号为1-10的球中任意抽取一个，取得的编号值被2或3整除的概率为（ ）。

    A：1/2
    B：3/10
    C：7/10
    D：1/10

    答案：C
    解析：

  • 第19题：

    概率为0的事件是不可能事件，概率为1的事件是必然事件。


    正确答案:错误

  • 第20题：

    一批产品共有10个正品和2个次品，任意抽取两次，每次抽一个，抽出后不再放回，则第二次抽出的是次品的概率为（）.


    正确答案:2/5

  • 第21题：

    给定事件E的概率为0.31，则事件E的补的概率（）。

    • A、根据以上信息不能确定
    • B、可以是0和1之间的任意值
    • C、是0.69
    • D、是0.31

    正确答案:C

  • 第22题：

    接受概率L（P）=PO+P1+P3...=ΣP，式中PO的含义为（）。

    • A、样本合格数为0的抽取概率
    • B、样本中不合格数为0的抽取概率
    • C、产品中合格数为0的抽取概率
    • D、产品中不合格数为0的抽取概率

    正确答案:B

  • 第23题：

    单选题
    一批产品共有十个正品和2个次品。任意抽取两次，每次抽取一个后不再放回。则第二次抽取的是次品的概率是（）。
    A

    1/5

    B

    六分之一

    C

    十一分之一

    D

    十二分之一


    正确答案： C
    解析： 暂无解析

  • 第24题：

    单选题
    接受概率L（P）=PO+P1+P3...=ΣP，式中PO的含义为（）。
    A

    样本合格数为0的抽取概率

    B

    样本中不合格数为0的抽取概率

    C

    产品中合格数为0的抽取概率

    D

    产品中不合格数为0的抽取概率


    正确答案： C
    解析： 暂无解析

相关内容