itgle.com
某校有58名同学参加数学竞赛，已知将参赛人任意分成四组，则必有一组的女生多于3人，又知参赛者中任意14人中必有男生，则参赛男生的人数为： A45 B46 C47 D48
题目
A45
B46
C47
D48
相似考题
更多“某校有58名同学参加数学竞赛，已知将参赛人任意分成四组，则必有一组的女生多于3人，又知参赛者中任意14人中必有男生，则参赛男生的人数为： ”相关问题
-
第1题：
某校参加数学竞赛有120名男生、80名女生，参加语文竞赛有120名女生、80名男生。已知该校总共有260名学生参加了竞赛，其中有75名男生两科竞赛都参加了，那么只参加数学竞赛而没有参加语文竞赛的女生有多少人?
A．15
B．25
C．65
D．75
正确答案：A
[答案] A。[解析]此题为比较复杂的容斥问题，有75名男生两科竞赛都参加了，因此至少参加了一项竞赛的男生有120+80-75=125人，那么至少参加一项竞赛的女生有260-125=135人，那么只参加数学竞赛没有参加语文竞赛的女生有135-120=15人。 -
第2题：
某校参加数学竞赛的有120名男生，80名女生，参加语文竞赛的有120名女生，80名男生。已知该校总共有260名学生参加了竞赛，其中有75名男生两科都参加了，问只参加数学竞赛而没有参加语寒竞赛的女生有多少人?（ ）
A．65
B．60
C．45
D．15
正确答案：D
依题意可知，同时参加两种竞赛的人数是(120+80)×2-260=140(人)，同时参加两种竞赛的女生人数是为140-75=65（人)．则只参加了数学而未参加语文竞赛的女生有80-65=15(人)。故选D。 -
第3题：
某校有 58 名同学参加数学竞赛，已知将参赛人任意分成四组，则必有一组的女生多于3 人，又知参赛者中任意 14 人中必有男生，则参赛男生的人数为：
A.45
B.46
C.47
D.48答案：A解析：由题干中必有一组女生多于3人，根据最不利原则可知，四组女生最少人数为3×4＋1＝13人，而又根据任意14人中必有男生得知，女生人数不超过13人，则可确定女生人数就是13人。总人数为58人，男生45人，所以选择A。 -
第4题：
育红小学六年级举行数学竞赛，参加竞赛的女生比男生多28人。根据成绩，男生全部
获奖，而女生则有25％的人未获奖。获奖总人数是42人，又知参加竞赛的人数占全年级的
2/5，,六年级学生共有多少人?A.120
B.125
C.130
D.135答案：C解析：设有x个女生参赛，由题意可得，(x一28)+(1—25％)x＝42，解得x＝40，参赛人数为(x一28)+x=52人。六年级学生共有52÷=130人，应选择C。 -
第5题：
育红小学六年级选出的男生的
和12名女生参加数学竞赛，剩下的男生人数是剩下的女生人数的2倍。已知六年级共有156人，问男、女生各有多少人？（ ）
A. 99，57
B. 96，60
C. 86，70
D. 80，76答案：A解析：
-
第6题：
参加某次数学竞赛的女生和男生人数的比是1:3，这次竞赛的平均成绩是82分，其中男生的平均成绩是80分，女生的平均成绩是（ ）
A、82 分
B、86 分
C、87 分
D、 88 分答案：D解析：设女生的平均成绩是x。由题意得，x×1+3×80 = 82×(1+3)，解得x= 88，故女生的平均成绩是88分。 -
第7题：
某高中只有文科班和理科班，男生人数比女生多，理科班人数比文科班多。根据以上条件，可以判断下列说法必定为真得是（）。
- A、文科班的男生总人数多于文科班的女生总人数
- B、理科班的男生总人数多于理科班的女生总人数
- C、文科班的男生总人数多于理科班的女生总人数
- D、理科班的男生总人数多于文科班的女生总人数
正确答案:D -
第8题：
某班有若干人参加拔河比赛，任意分成5组，总会至少有一组的女生多于3人，那么参赛 女生至少有几人（）
- A、15
- B、16
- C、17
- D、18
正确答案:B -
第9题：
单选题据统计，去年在某校参加高考的385名文、理科考生中，女生189人，文科男生41人，非应届男生28人，应届理科考生256人。由此可见，去年在该校参加高考的考生中（）A非应届文科男生多于20人。
B应届理科女生少于130人。
C应届理科男生多于129人。
D应届理科女生多于130人。
E非应届文科男生少于120人。
正确答案： B解析： 暂无解析 -
第10题：
某校参加数学竞赛的有120名男生，80名女生，参加语文竞赛的有120名女生，80名男生。已知该校总共有260名学生参加了竞赛，其中有75名男生两科都参加了，问只参加数学竞赛而没有参加语文竞赛的女生有多少人?（ ） A．65 B．60 C．45 D．15
正确答案：D
依题意可知，同时参加两种竞赛的人数是(120+80)×2—260=140(人)，同时参加两种竞赛的女生人数为140—75=65(人)，则只参加了数学而未参加语文竞赛的女生有80—65=15(人)。故选D。
-
第11题：
现从8名学生干部中选出2名男同学和1名女同学分别参加全校“资源”、“生态”和“
环保”三个夏令营活动，已知共有90种不同的方案，那么男、女同学分别有A: 男生5人，女生3人
B: 男生3人，女生5人
C: 男生6人，女生2人
D: 男生2人，女生6人答案：B解析：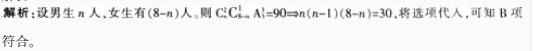
-
第12题：
某高中826 名新生入校进行宿舍分配，已知女生寝室分配每间4 人还剩2 人，男生寝室分配每间6人还剩4 人，男生寝室数比女生寝室数多20 间，则新生中共有男生（ ）人。A.262
B.564
C.544
D.282答案：C解析：设男生寝室数为x 间，则6x+4x-4×20=826-2-4=820，x=90 间，所以男生人数=6×90+4=544 人，故答案为C。 -
第13题：
—次校友聚会共有50人参加，在参加聚会的同学中，每个男生认识的女生人数各不相同，而且恰好构成一串连续的自然数。已知认识女生最少的一个男生认识15名女生，并有一名男生认识所有女生，则参加这次聚会的男生一共有：A.16 名
B.17 名
C.18 名
D.19 名答案：C解析：设共有x名男生，则有女生50-x名，认识女生最多的一名男生认识x-1+15名女生，则有x-1+15=50-x，解得x=18。 -
第14题：
据统计，去年在某校参加高考的385名文理考生中，女生189人，文科男41人，非应届男生28人，应届理科生256人，由此可见，去年在该校参加高考的考生中：A.非应届文科男生多于20人
B.应届理科女生少于130人
C.非应届文科男生少于20人
D.应届理科女生多于130人
E.应届理科xxx答案：B解析： -
第15题：
据统计，去年在某校参加高考的385名文、理科考生中，女生189人，文科男生41人，非应届男生28人，应届理科考生256人。由此可见，去年在该校参加高考的考生中（）
- A、非应届文科男生多于20人。
- B、应届理科女生少于130人。
- C、应届理科男生多于129人。
- D、应届理科女生多于130人。
- E、非应届文科男生少于120人。
正确答案:B -
第16题：
某校有55个同学参加数学竞赛，已知若参赛人员任意分成四组，则必然有一组的女生多于2人，又知参赛者中任何10人中必有男生，则参赛男生的人数为（）人。
- A、42
- B、46
- C、47
- D、48
正确答案:B -
第17题：
单选题某校有55个同学参加数学竞赛，已知若参赛人员任意分成四组，则必然有一组的女生多于2人，又知参赛者中任何10人中必有男生，则参赛男生的人数为（）人。A42
B46
C47
D48
正确答案： D解析： 任意分成四组，必有一组的女生多于2人，所以女生至少有4×2+1=9人，任意10人中必有男生，则女生人数至多有9人，则男生有55-9=46人，选B。