itgle.com
设x1,x2,…,x9是从正态总体N(μ，0.62)中随机抽取的样本，样本均值为，μa是标准正态 分布的a分位数，则均值μ的0.90置信区间为（ ）。 A. ±0.2u0.95 B.±0.2u0.90 C. ±0.6u0.90 D.±0.6u0.95
题目
，μa是标准正态 分布的a分位数，则均值μ的0.90置信区间为（ ）。
A.
±0.2u0.95 B.
±0.2u0.90 C. 
±0.6u0.90 D.
±0.6u0.95相似考题
更多“设x1,x2,…,x9是从正态总体N(μ，0.62)中随机抽取的样本，样本均值为，μa是标准正态 分布的a分位数，则均值μ的0.90置信区间为（ ）。 ”相关问题
-
第1题：
对正态总体参数的估计描述正确的是（ ）。
A.正态均值μ的无偏估计有两个，一个是样本均值的估计，另一个是样本中位数的估计，即
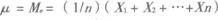
B.对正态均值μ来说，样本均值总比样本中位数更有效，应舍去样本中位数
C.在实际过程中，应优先选用样本均值去估计正态均值μ。但有时在现场，为了简便快捷，选用样本中位数去估计正态均值μ也是有的
D.正态方差σ2的无偏估计常用的只有一个，就是样本方差S2
E.正态方差σ2的无偏估计常用的只有一个，就是样本方差X2
正确答案：CD
-
第2题：
设(X1，X2，…，Xn)是来自正态总体N(μ，σ2)的简单随机样本，其中参数μ，σ2未知，则下列各项中，不是统计量的有( )。
正确答案：DE
解析：统计量中不含有任何未知参数，故D、E项不是统计量。 -
第3题：
设Xi＝(i＝1，2，…，16)为正态总体N(0，4)的样本，
为样本均值，则的分布可以表示为( )。
正确答案：CD
解析：对于样本均值的正态分布的均值为0，标准差σ为故其分布可用C来表示；同样地对于μ＝0，σ＝1/2代入概率密度函数的公式会发现选项D也是正确的。 -
第4题：
从正态总体X～N（0,σ^2）中抽取简单随机样本X1,X2,…,Xn,则可作为参数σ^2的无偏估计量的是().
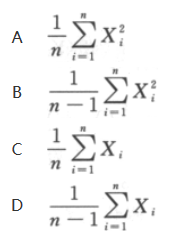答案：A解析：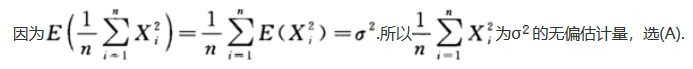
-
第5题：
设X1，X2，…，Xn是来自正态总体N(μ，σ2)的一个样本，，s2分别是样本均值和样本方差，令，则有( )。A、W～t(n)
B、W～t(n-1)
C、W～F(n)
D、W～F(n-1)答案：B解析：由常用的统计量的分布知W～t(n-1) -
第6题：
正态标准差σ的1一α置信区间依赖于（ ）。
A.样本均值 B.样本方差
C.样本标准差 D. t分布的分位数
E. X2分布的分位数答案：B,C,E解析：
然它依赖于样本标准差s (或样本方差）和X2分布的分位数。 -
第7题：
从正态总体N(10，12)中随机抽出样本为4的样本，则样本均值的标准差为（）。
A. 0.5 B. 1 C. 2 D. 4答案：A解析：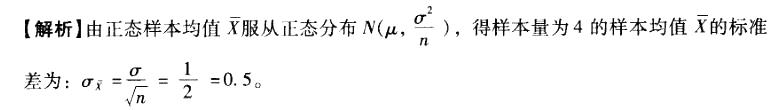
-
第8题：
设总体X服从正态分布N(μ，σ^2)(σ>0)，从该总体中抽取简单随机样本X1，X2，…，Xn(n≥2)，其样本均值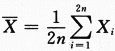
,求统计量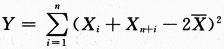
的数学期望E(Y).答案：解析：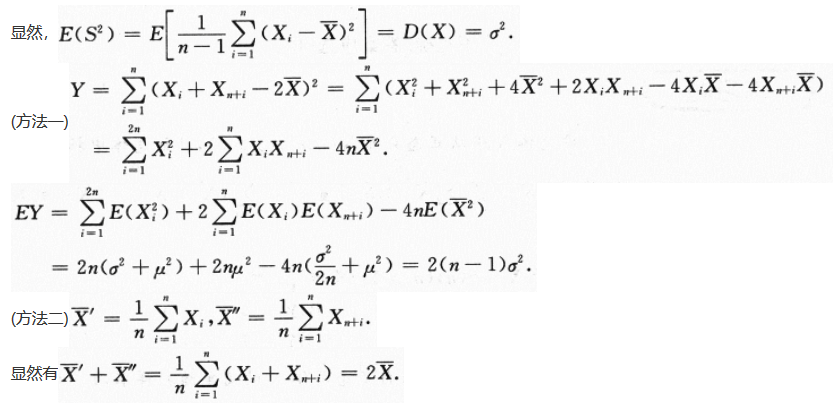
-
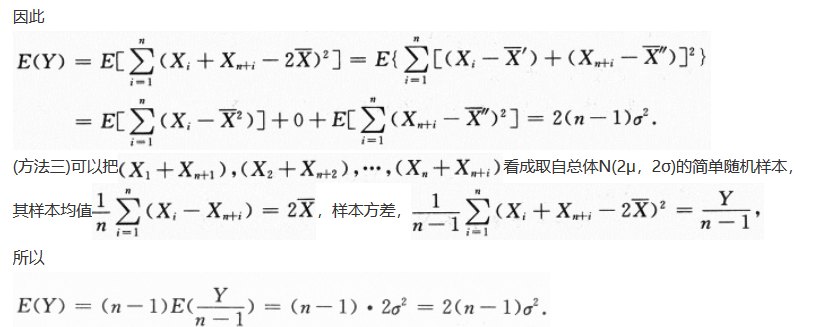
第9题：
已知总体分布为正态，方差未知。从这个总体中随机抽取样本容量为65的样本，样本平均数 为60，样本方差为100，那么总体均值 的99%的置信区间为A.[ 56.775 ,63.225]
B.[53.550,66.450]
C.[56.080,63.920]
D.[57.550,62.450]答案：A解析：本题考查的是总体平均数的估计方法。当总体方差未知时，若总体分布为正态，或者总体分布为非正态，但样本容量超过30，置信区间的公式是：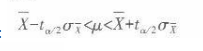
因为总体方差未知，可通过如下公式计算标准误：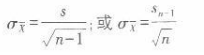
当n>30时，t分布渐近正态分布，在不查表的情况下也可用
作近似计算。将本题中各项数据代入，求得置信区间为[ 56.775，63.225]。因此本题选A。 -
第10题：
设样本x1，x2，…，xn来自正态总体N（0，9），其样本方差为s2，则E（s2）=（）
正确答案:9 -
第11题：
关于中心极限定理的描述正确的是：（）。
- A、对于n个相互独立同分布的随机变量共同服从正态分布，则样本均值又仍为正态分布
- B、正态样本均值服从分布N（μ，σ2/n）
- C、设X1，X2，„，Xn为n个相互独立共同分布随机变量，其共同分布不为正态分布或未知，但其均值和方差都存在，则在n相当大时，样本均值近似服从正态分布
- D、无论共同分布是什么，只要变量个数n相当大时，均值的分布总近似于正态分布
正确答案:A,B,C,D -
第12题：
多选题已知正态总体标准差为10，样本量n=25，置信水平为95%，Z=1.96，样本均值=105.36。则以下正确的有（）A样本均值的标准差为10
B样本均值的标准差为2
C样本均值的置信区间为（101.44，109.28）
D总体均值的置信区间为（101.44，109.28）
正确答案： D,C解析： 暂无解析 -
第13题：
设X1，X2，…，Xn是来自正态总体N(μ，σ2)的一个样本，
与s分别为其观测值的样本均值与样本标准差，则在下列抽样分布中正确表述的有( )。
正确答案：AD
解析：设X1，X2，…，Xn是来自正态总体N(μ，σ2)一个样本，则，对样本均值施行标准化变换，则有：。当用样本标准差s代替中的σ时，有。 -
第14题：
设X～N(μ，0.09)从中随机抽取样本量为4的样本，其样本均值为
，则总体均值μ的 0.95的置信区间为( )。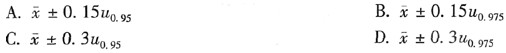
正确答案：B
解析：由X～N(μ，0.09)可知该总体标准差已知，用正态分布得μ的1-α的置信区间为。所以μ的0.95的置信区间=。 -
第15题：
设(X1,X2,…,Xn)（N≥2）为标准正态总体X的简单随机样本,则().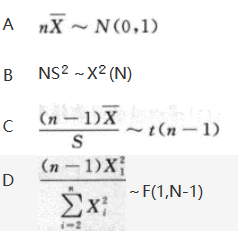
答案：D解析：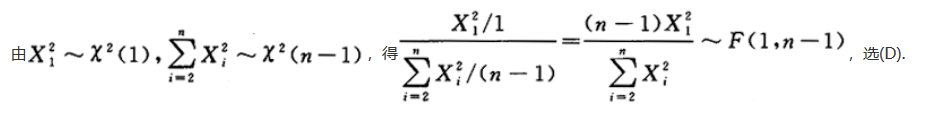
-
第16题：
设总体X～N（μ,σ^2）,X1,X2,…,Xn为总体X的简单随机样本,X与S^2分别为样本均值与样本方差,则().
答案：A解析：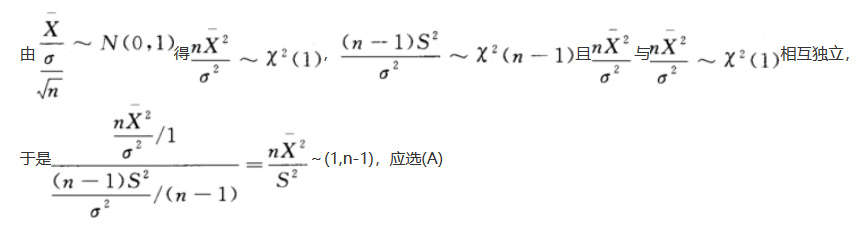
-
第17题：
从正态总体N (10，22)中随机抽出样本量为4的样本，则样本均值的标准差为( )。
A. 4 B. 2
C. 1.5 D. 1答案：D解析：。σx=2，则样本量为4的样本均值的方差为22/4 = 1。 -
第18题：
正态总体标准差的置信区间的宽度依赖于（ ）。
A.样本标准差
B.样本量
C.样本均值
D.t分布的分位数
E.置信度答案：A,B,E解析：
-
第19题：
设正态总体X的方差为1,根据来自总体X的容量为100的简单随机样本测得样本的均值为5,则总体X的数学期望的置信度近似等于0.95的置信区间为_______.答案：1、(4.804 2、5.196)解析：X～N（μ，1），取统计量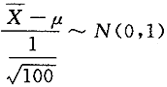
，则μ的置信度为0.95的置信区间为 
-
第20题：
设X1，X2，…，X9是来自正态总体X的简单随机样本，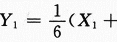
…
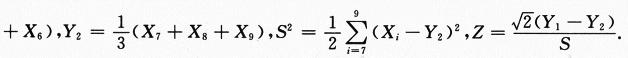证明统计量Z服从自由度为2的t分布.
答案：解析：
-
第21题：
已知总体分布为正态，方差为100。从这个总体中随机抽取样本容量为16的样本，样本平均数为60，那么总体均值 的99%的置信区间为A.[50.10,69.90]
B.[53.55,66.45]
C.[56.08,63.92]
D.[55.10,64.90]答案：B解析：本题考查的是总体平均数的估计方法。当总体方差已知时，若总体分布为正态，或者总体分布为非正态，但样本容量超过30，置信区间的公式是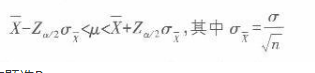
将本题中各项数据代入，则求得置信区间为[ 53.55，66.45]。 -
第22题：
已知正态总体标准差为10，样本量n=25，置信水平为95%，Z=1.96，样本均值=105.36。则以下正确的有（）
- A、样本均值的标准差为10
- B、样本均值的标准差为2
- C、样本均值的置信区间为（101.44，109.28）
- D、总体均值的置信区间为（101.44，109.28）
正确答案:B,D -
第23题：
单选题从一个均值为µ，方差为σ²的正态总体中抽取样本，则（ ）。A样本均值一定服从正态分布
B样本均值一定服从t分布
C样本均值一定服从卡方分布
D样本均值一定服从F分布
正确答案： A解析：