itgle.com

为提高某化工产品的产量，用L8(27)安排的一个正交试验，各因子的偏差平方和如表所示。A与B各水平组合下试验结果均值如表所示。A、B、C和D各因子每一水平下的试验均值如表所示。当a=0.05时，F检验的临界值为F0.95(1, 2)=18.5，下列结论正确的有（）。 A.因子A,B均显著 B.交互作用AxB不显著 C.因子C, D均不显著 D.最优搭配为A1B2C2D2

题目
为提高某化工产品的产量，用L8(27)安排的一个正交试验，各因子的偏差平方和如表所示。A与B各水平组合下试验结果均值如表所示。A、B、C和D各因子每一水平下的试验均值如表所示。

当a=0.05时，F检验的临界值为F0.95(1, 2)=18.5，下列结论正确的有（）。
A.因子A,B均显著
B.交互作用AxB不显著
C.因子C, D均不显著
D.最优搭配为A1B2C2D2

相似考题

1.05时，F检验的临界值为F0.95(1，2)=18.5，下列结论正确的有( )。A．因子A，B均显著B．交互作用A×B不显著C．因子C，D均不显著D．最优搭配为A1B2C2D2/

2.已知单因子试验的方差分析表如表2.1—6所示，则下列结论正确的有( )。A．因子A的水平为3B．误差平方和的自由度为12C．各水平下试验指标的方差估计值为20D．在α=0.01的水平下，因子A不显著E．在α=0.01的水平下，因子A显著

3.为提高某化工产品的产量，用L8(27)安排的一个正交试验，各因子的偏差平方和如表 2.3-12所示。误差的自由度为( )。A．1B．2C．7D．8

4.在一个用L9(34)安排的正交设计中，表头设计与各列平方和如表2.3-5所示，从F分布表查得F0.90(2，2)=9.0，F0.95(2，2)=19.0，则有( )。A．Se=S4B．三个因子都是显著的C．在显著性水平0.1上因子A是显著的D．在显著性水平0.05上因子B是显著的E．在显著性水平0.05上因子C是显著的

更多“为提高某化工产品的产量，用L8(27)安排的一个正交试验，各因子的偏差平方和如表所示。A与B各水平组合下试验结果均值如表所示。A、B、C和D各因子每一水平下的试验均值如表所示。 当a=0.05时，F检验的临界值为F0.95(1, 2)=18.5，下列结论正确的有（）。 A.因子A,B均显著 B.交互作用AxB不显著 C.因子C, D均不显著 D.最优搭配为A1B2C2D2”相关问题

  • 第1题：

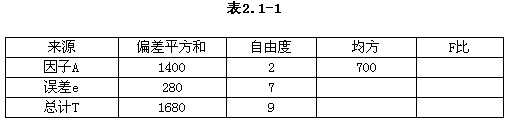
    已知单因子试验的方差分析表，如表2.1—1所示，则下列结论正确的是( )。

    A．因子A的水平数为2

    B．误差e的均方为700

    C．各水平下试验指标的方差估计值为40

    D．FA=100


    正确答案：C
    解析：由题意可知，因子A的自由度为2，水平数为3；误差e的均方MSe=280/7=40，即各水平下试验指标的方差估计值=40；因子A的均方MSA=700，则FA=MSA/MSe=700/40=17.5。

  • 第2题：

    为提高某化工产品的性能指标，选择三个因子A，B，C，每个因子各取3个水平，并用正交表L9(34)安排试验(见表2.3-10表头)，根据9个试验结果可算得各水平对应的试验结果之和如表2.3-10所示。

    用极差对因子主次排序，结果是( )。

    A．A，B，C

    B．A，C，B

    C．C，A，B

    D．C，B，A


    正确答案：B
    解析：因子A，B，C的极差分别为RA=63-3=60，RB=39-24=15，RC=57-9=48，极差越大，因子对指标的影响越强。则排序结果为A、C、B。

  • 第3题：

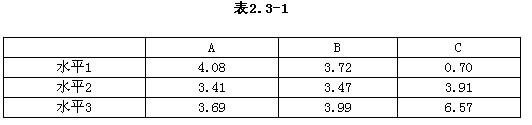
    为提高某产品的质量指标，需考虑3个三水平因子：A、B、C，把这3个因子依次安排在正交表L9(34)的前三列上，通过试验和计算获得各列各水平的平均值如表2.3-1所示。在质量指标愈大愈好的场合，利用直观分析应选取的较好因子水平组合是( )。

    A．A1B3C3

    B．A2B2C1

    C．A1B1C3

    D．A3B3C3


    正确答案：A
    解析：由于要求质量高，因此在每一因子各平均值中找一个最大值对应的水平，将它们组合起来便可以得到。从表可知，因子A中最大值对应的水平为A1，因子B中最大值对应的水平为B3，因子C中最大值对应的水平为C3，故应取为A1B3C3。

  • 第4题：

    在单因子方差分析中，因子A是二水平的，在每一水平下重复进行了3次试验，结果如表所示，则下列结论正确的有（ ）。

    A.误差平方和Se =4 B.因子A的平方和SA =24
    C.误差均方MSe =2 D.因子A的均方MSA= 12
    E.统计量F=24


    答案：A,B,E
    解析：

  • 第5题：

    用正交表安排试验时，通过方差分析发现因子A及交互作用AXB都是显著的，但C、D是不显著的，那么应按（ ）寻找最好条件。
    A.找出因子D的最好水平 B.找出因子A的最好水平
    C.找出因子A与B的最好水平搭配 D.找出因子C的任意水平
    E.找出因子C与D的最好水平搭配


    答案：C,D
    解析：
    当交互作用AXB显著时，不管因子A与B本身是否显著，需要从A与B的水平搭配中找最好的，对不显著因子可以找任意水平。

  • 第6题：

    为提高某化工产品的性能指标，选择三个因子A,B, C,每个因子各取3个水平，并用正交表L9(34)安排试验，根据9个试验结果可算得各水平对应的试验结果之和如表所示。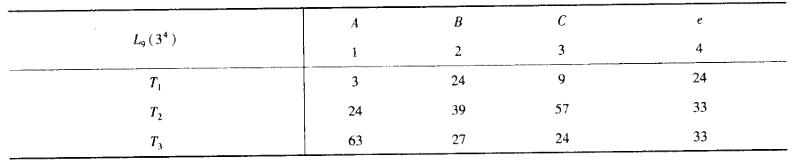


    已算得L9(34)表中各列的平方和为S1=618, S2 =42, S3 =402，S4=18。则各因子及误差的均方分别是（ ）。
    A. MSA =309 B. MSB =57
    C. MSC =201 D. MSe =9


    答案：A,C,D
    解析：
    因子A、B、C分别置于第一列、第二列和第三列，SA=S1，SB=S2, SC=S3, Se=S4,而因子A、B、C的自由度均为2,则MSA= SA/fA=618/2 = 309,同理可得MSB = 21，MSC=201；而误差的自由度为正交表上空白列的自由度相加，所以fe=2，MSe=Se/fe=9。

  • 第7题：

    为提高某产品的产量，考虑三个三水平因子：反应温度(A)，反应压力(B)，溶液浓度 (C)。当用正交表L9(34)安排试验时，因子A、B、C依次放在1、2、3列上，并且通过试验得到各列的极差，如表所示，则各因子对指标的影响程度从大到小为（ ）。

    A. C、B、A B. C、A、 B C. B、A、C D. A、B、C


    答案：B
    解析：
    各因子对指标的影响程度的大小可以按极差从大到小排列得到。由表可得，
    Rc=5. 87 >RA =0.67 >RB=0.62，因此各因子对指标的影响程度从大到小为C、A、B。

  • 第8题：

    为提高某化工产品的产量，用L8(27)安排的一个正交试验，各因子的偏差平方和如表所示。A与B各水平组合下试验结果均值如表所示。A、B、C和D各因子每一水平下的试验均值如表所示。

    误差的自由度为（ ）。
    A. 1 B. 2 C. 7 D. 8


    答案：B
    解析：
    正交表Ln(qp)，当表中行数n、列数p与水平数q满足n=qk, k=2, 3, 4，…；
    p =(n-1)/(q-1)时，对离差平方和有关系式ST=S1+S2+…+Sp，同样对自由度也有相应关系式：fT=f1+f2+…+fp=n-1。由题意，正交表L8(27)满足要求，且各因子水平数为2，所以fA=fB=fC=fD=fAXB=1，因此，fT=n-1=8-1=7，误差自由度fe =fT-fA-fB-fC-fD-fAXB=7-5 =2。

  • 第9题：

    已知单因子试验的方差分析表如表所示，则下列结论正确的有（ ）。

    A.因子A的水平为3
    B.误差平方和的自由度为12
    C.各水平下试验指标的方差估计值为20
    D.在a=0.01的水平下，因子A不显著
    E.在a=0.01的水平下，因子A显著


    答案：B,C,E
    解析：
    由题意，因子A的离差平方和SA1200，离差平方和的自由度fA=3，因子A的水平为4；误差平方和Se=240，误差平方和的自由度fe= 12；各水平下试验指标的方差估计值MSe =20；因为F = 20 >5. 95，所以在a =0.01的水平下，因子A显著。

  • 第10题：

    有3个二水平因子A、B、C及其交互作用A xC需要考察。用L8 (27)安排试验，表头设计与各列平方和如表所示。则检验交互作用AxC是否显著的统计量F的值为 ( )。


    A. 9.01 B. 16. 22 c ；.57. 52 D. 20. 58


    答案：D
    解析：
    根据题意知，SA=S1= 53. 7, SB=S2 =78.2, SC=S4 =703.1，第5列的表头为AxC，所以交互作用平方和也为其所在列的平方和，记为S AxC=S5 =253.1，S AxC的自由度fAxC为两因子自由度的乘积，即为1。由于第3、6、7列为空白列，所以误差平方和可以用这三列平方和之和来表示，即： Se =S3 +S6 +S7 =5.7 +3. 1 +28. 1 =36.9，其自由度为三列自由度的和，即fe = 3。所以MSAxC = SAxC/fAxC = 253. 1/1 = 253. 1，MSe = Se/fe = 36.9/3=12.3，则检验交互作用AxC是否显著的统计量F的值为：F = MSAxC/MSe = 253. 1/12. 3≈20. 58。

  • 第11题：

    为了使某橡肢阀座的硬度指标y满足76±3，进行配方调整试验，着重考察4个因子A、 B、C、D及交互作用AxB，每个因子取两个水平，选用L8(27)正交表。试验方案设计及根据试验所得数据的计算结果如表所示。由于要求硬度指标y适中为好，所以表下方T1、T2、S的数值是通过y'= y-76 变换后的数据计算而得。因此对y'而论，要求愈小愈好。试回答以下问题。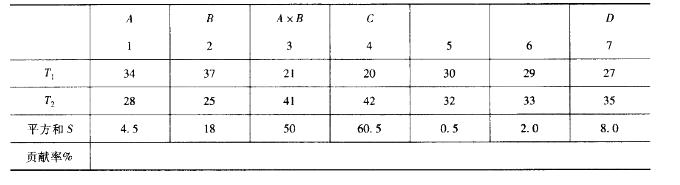


    取显著性水平a=0. 10，F检验临界值F0.90(1，2) =8.53，则对硬度指标有显著影响的因子是（ ）。
    A. A, B, C B. C, A xB, B, D
    C. C, AxB D. C, A xB, B


    答案：D
    解析：
    由题意，各因子水平数为2，所以 fA=fB=fc=fD=fAxB=1，误差平方和的自由度是空白列自由度之和，所以fe=2，误差平方和是空白列平方和之和，所以Se =2.5,则:

  • 第12题：

    为提高某产品的质量指标，需考虑3个三水平因子：A、B、C，把这3个因子依次安排在正交表L9(34)的前三列上，通过试验和计算获得各列各水平的平均值如表所示。在质量指标愈大愈好的场合，利用直观分析应选取的较好因子水平组合是（ ）。

    A. A1B3C3 B. A2B2C1 C. A1B1C3 D. A3B3C3


    答案：A
    解析：
    由于要求质量高，因此在每一因子各平均值中找一个最大值对应的水平，将它们组合起来便可以得到。从表可知，因子A中最大值对应的水平为A1，因子B中最大值对应的水平为B3，因子C中最大值对应的水平为C3，故应取为A1B3C3。

  • 第13题：

    在一个L8(27)正交试验中，因子A、B、C、D的F比如表2.3-7所示，则辨别因子的显著性情况为( )。

    A．A因子(在6=0.05)为显著

    B．B因子(在α=0.01)为显著

    C．B因子(在α=0.05)为显著

    D．C因子(在α=0.01)为显著

    E．D因子为不显著


    正确答案：ACDE
    解析：由题意，FA=12.96；FB=15.85；FC=43.15；FD=1.55。因为F0.95(1，3)FAF0.95(1，3)；F0.95(1，3)FBF0.95(1，3)；FC＞F0.99(1，3)；FDF0.95(1，3)，所以A因子(在α=0.05)显著，B因子(在α=0.05)显著，C因子(在α=0.01)显著，D因子为不显著。

  • 第14题：

    在一个用L9(34)的正交试验中，各列的偏差平方和如表2.3-6所示，给定F0.90(2，2) =9.0、F0.95(2，2)=19.0，下列与本数据结果有关的正确项有( )。

    A．A、B、C为显著(α=0.05)

    B．A因子(α=0.10)显著

    C．B因子(α=0.05)显著

    D．S4≠Se

    E．C因子(α=0.05)不显著


    正确答案：BCE
    解析：由题意，因子水平数均为3，SA=1320，SB=5110，SC=468，Se=88，其中，S4=Se；fA=fB=fC=2，fe=2。则，同理可得FB=58.07，FC=5.32，因为F0.95(2，2)FAF0.95(2，2)；FB＞F0.95(2，2)；FCF0.90(2，2)，所以A因子(α=0.10)显著，B因子(α=0.05)显著，C因子都不显著。

  • 第15题：

    在单因子方差分析中，因子A是二水平的，在每一水平下重复进行了3次试验，结果如表2.1-2所示，则下列结论正确的有( )。

    A．误差平方和Se=4

    B．因子A的平方和SA=24

    C．误差均方MSe=2

    D．因子A的均方MSA=12

    E．统计量F=24


    正确答案：ABE
    解析：

  • 第16题：

    为提高某化工产品的性能指标，选择三个因子A,B, C,每个因子各取3个水平，并用正交表L9(34)安排试验，根据9个试验结果可算得各水平对应的试验结果之和如表所示。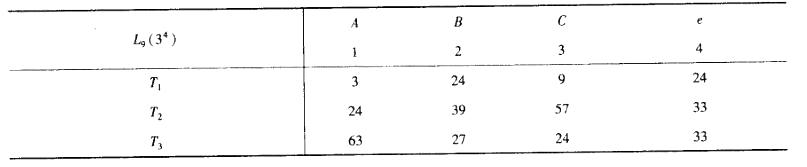


    用直观分析法，使性能指标愈大愈好的最佳水平条件是（ ）。
    A. A3B1C1 B. A3B2C1 C. A3B2C2D. A3B2C3


    答案：C
    解析：
    根据题意可知，对于因子A有：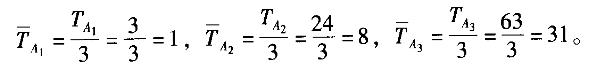

    则因子A的三水平好；同理可得因子B的二水平好，因子C的二水平好，所以使性能指标愈大愈好的最佳水平条件是A3B2C2。

  • 第17题：

    为提高某化工产品的性能指标，选择三个因子A,B, C,每个因子各取3个水平，并用正交表L9(34)安排试验，根据9个试验结果可算得各水平对应的试验结果之和如表所示。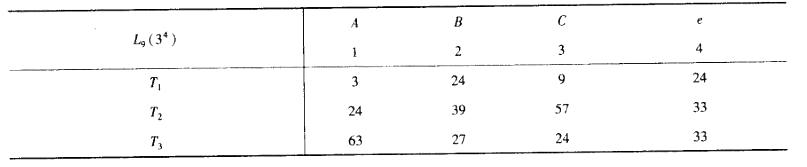


    若取a=0.05，查表得F0.95(2，2) =19.0，则显著因子有（ ）。
    A. A； B； C B. A； B C. A； C D. B； C


    答案：C
    解析：
    据题意可得，FA= MSA/MSe = 309/9≈34. 33 > 19. 0 , FB = MSB/MSe = 21/9≈2. 33 c = MSc/MSe = 201/9 ≈22. 33 > 19. 0 ,所以因子A、C 为显著因子。

  • 第18题：

    为提高某化工产品的性能指标，选择三个因子A,B, C,每个因子各取3个水平，并用正交表L9(34)安排试验，根据9个试验结果可算得各水平对应的试验结果之和如表所示。


    用极差对因子主次排序，结果是（ ）。
    A. A, B,C B. A, C,B
    C. C,A, B D. C, B,A


    答案：B
    解析：
    因子A,B,C的极差分别为RA=63-3 = 60, RB=39 -24 =15，RC=51 -9 =48，极差越大，因子对指标的影响越强。则排序结果为A、C、B。

  • 第19题：

    考察温度对某一化工产品得率的影响，特选5种不同温度进行试验，并在同一温度下各进行3次重复试验，试验结果如表所示。


    若取显著性水平a =0.05，査F分布表得临界值是3. 48，则（ ）。
    A.因子A显著 B.因子A不显著
    C.误差方差σ2的估计为5 D.误差方差σ2的估计为12. 5


    答案：A,C
    解析：
    由于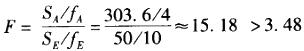，所以因子A显著；误差方差σ2的估计为：MSE= SE/fE =50/10 =5 。

  • 第20题：

    已知单因子试验的方差分析表，如表所示，则下列结论正确的是（ ）。

    A.因子A的水平数为2
    B.误差e的均方为700
    C.各水平下试验指标的方差估计值为40
    D. FA= 100


    答案：C
    解析：
    由题意可知，因子A的自由度为2，水平数为3；误差e的均方MSe=280/7 =40， 即各水平下试验指标的方差估计值=40；因子A的均方MSA =700，则FA=MSA/MSe = 700/40 = 17.5。

  • 第21题：

    在一个用L9(34)安排的正交设计中，表头设计与各列平方和如表所示，从F分布表查得 F0.90(2, 2) =9.0, F0.95(2,2) =19.0，则有（ ）。

    A. Se=S4
    B.三个因子都是显著的
    C.在显著性水平0. 1上因子A是显著的
    D.在显著性水平0. 05上因子B是显著的
    E.在显著性水平0. 05上因子C是显著的


    答案：A,C,D
    解析：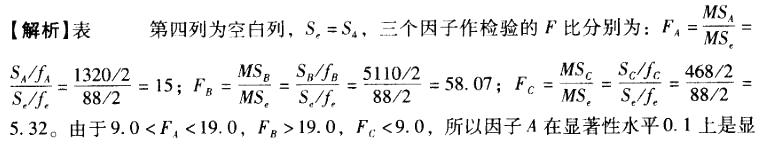

    著的，因子B在显著性水平0.05上是显著的。对于显著性水平0. 1和0.5，因子C都是不显著的。

  • 第22题：

    在一个L8(27)正交试验中，因子A、B、C、D的F比如表所示，则辨别因子的显著性情况为（）。


    A. A因子（在a =0. 05）为显著
    B. B因子（在a =0.01）为显著
    C. B因子（在a =0.05）为显著
    D. C因子（在a =0.01）为显著
    E. D因子为不显著


    答案：A,C,D,E
    解析：
    由题意，FA =12. 96, FB = 15. 85 ,FC=43. 15, FD= 1.55。又 F0.95(1，3) A0.99(1，3)； F0.95(1，3)B 0.99(1，3)； FC >F0.99(1，3)； FD0.95(1，3)，所以4因子（在a =0.05）显著，B因子（在a=0.05）显著，C因子（在a = 0. 01）显著，D 因子为不显著。

  • 第23题：

    在一个用L9(34)的正交试验中，各列的偏差平方和如表所示，给定F0.90(2,2)=9.0、F0.95(2, 2) = 19.0，下列与本数据结果有关的正确项有（ ）。

    A. A、B、C 为显著（a =0.05）
    B. A 因子（a =0. 10）显著
    C. B 因子（a =0.05）显著
    D. Se≠S4
    E. C因子(a= 0.05)不显著


    答案：B,C,E
    解析：
    由题意知，因子水平数均为3，SA= 1320, SB=5110, SC=468，Se=88，其中，Se=S4； fA=fB=fc=2，fe=2，则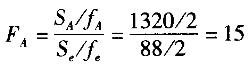，同理可得FB=58.07，FC =5.32，因为F0.90(2,2)A0.95(2,2)；FB>F0.95(2,2)； FC0.95(2,2)，所以A因子(a=0. 10)显著，B因子（a =0.05）显著，C因子都不显著。

相关内容