itgle.com
设X～N(1，4)，为样本容量n＝16的样本均值，则P(0＜≤2)为( )。A．2Φ(0.5-1)B．2Φ(2)-1C．2u0.5-1D．1-2Φ(2)
题目
设X～N(1，4)，
为样本容量n＝16的样本均值，则P(0＜≤2)为( )。
A．2Φ(0.5-1)
B．2Φ(2)-1
C．2u0.5-1
D．1-2Φ(2)
相似考题
更多“ 设X～N(1，4)，为样本容量n＝16的样本均值，则P(0＜≤2)为( )。A．2Φ(0.5-1)B．2Φ(2)-1C．2u0.5-1D．1-2Φ(2) ”相关问题
-
第1题：
正态分布计算所依据的重要性质为( )。
A．设X～N(μ,σ2)，则u=(X-μ)/σ～N(0，1)
B．设X～N(μ，σ2)，则对任意实数a、b有P(X＜b)=Ф[(b-μ)/σ)
C．设X～N(μ，σ2)，则对任意实数a、b有P(X＞a)=1-Ф[(a-μ)/σ]
D．设X～N(μ，σ2)，则对任意实数a、b有P(a＜X＜b)=Ф[(b-μ)/σ)-Ф[(a-μ)/σ]
E．设X～μ(μ1，
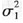，Y～N(μ2，
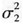，则X+Y～N(μ1+μ2，(σ1+σ2) 2)正确答案：ABCD
解析：若X～N(μ1，)，Y-N(μ2，)，X与Y相互独立，则(X+Y)～N(μ1，+μ2，+)。 -
第2题：
设Xi＝(i＝1，2，…，16)为正态总体N(0，4)的样本，
为样本均值，则的分布可以表示为( )。
正确答案：CD
解析：对于样本均值的正态分布的均值为0，标准差σ为故其分布可用C来表示；同样地对于μ＝0，σ＝1/2代入概率密度函数的公式会发现选项D也是正确的。 -
第3题：
设Xi=(i=1，2，…，16)为正态总体N(0，4)的样本，
为样本均值，则的分布可以表示为( )。A．N(0，1/2)
B．N(0，4)
C．N(0，1/4)
D．概率密度为
E．N(0，1/8)
正确答案：CD
解析：因Xi=(i=1，2，…，16)为正态总体N(0，4)的样本，所以其均值也服从正态分布，且均值为0，标准差为；将μ=0，σ=1/2代入正态分布的概率密度函数p(x)=，-∞x∞，可得的概率密度为。 -
第4题：
设 X、Y相互独立，X~N(4，1),Y~N(1，4),Z=2X-Y，则A.0
B.8
C. 15
D. 16答案：B解析：提示：由方差性质D(Z) =D(2X)+D(Y) = 4D(X)+D(Y) = 4x1 + 4。 -
第5题：
设总体X～N（μ,σ^2）,X1,X2,…,Xn为总体X的简单随机样本,X与S^2分别为样本均值与样本方差,则().
答案：A解析：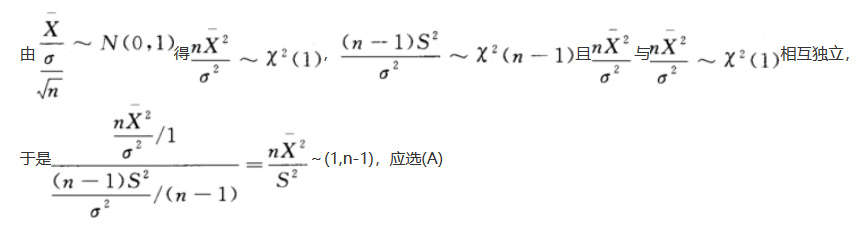
-
第6题：
设随机变量X?N(0，σ2)，则对于任何实数λ都有:
(A) P(X≤λ)=P(X≥λ)(B)P(X≥λ)= P(X≤-λ)
(C) X-λ~N(λ，σ2-λ2)(D)λX~N(0，λσ2)答案：B解析：解:选B。
排除错误选项。
X-λ~N(-λ，σ2)，选项C错误。
λX~N(0，λ2σ2)，选项D错误。 -
第7题：
设X~N(μ，σ2)，σ已知，xi为样本（i= 1，2，…，n）。 H0：μ=μ0 ， H1：μ≠μ0 ，则检验统计量指的是（ ）。
答案：B解析：对于单个正态总体，当总体方差σ2已知时，均值μ的检验统计量为
。 -
第8题：
设Xi=(i= 1, 2, …,16)为正态总体N(0，4)的样本，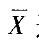
为样本均值，则
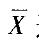的分布可以表示为（）。
A. N(0, 1/2) B. N(0, 4)C. N(0, 1/4)
E. N(0, 1/8)答案：C,D解析：
-
第9题：
设随机变量X～N(0,σ^2),Y～N(0,4σ^2),且P(X≤1,y≤-2)=
,则P（X>1,Y>-2）=_______.答案：解析：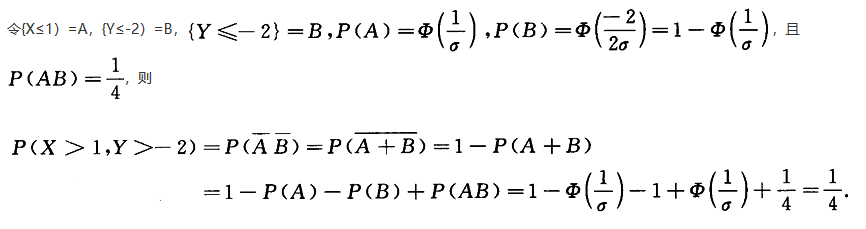
-
第10题：
设X~N（1，4），Φ（0.5）=0.6915，Φ（1.5）=0.9332则P{|X|>2}为（）
- A、0.2417
- B、0.3753
- C、0.3830
- D、0.8664
正确答案:B -
第11题：
问答题从总体X～N（μ，σ2）中抽取一个样本容量为16的样本，μ和σ2均未知，试求： （1）P{S2/σ2≤2.041}； （2）D（S2）。正确答案：
(1)由正态总体统计量的分布性质知(n-1)S2/σ2~χ2(n-1)(n=16)
所以P{S2/σ2≤2.041}=P{15S2/σ2≤15×2.041}=1-P{χ2(15)>30.615}=0.99
(2)由χ2的性质可知D(χ2(n))=2n,所以
D((n-1)S2/σ2)=(n-1)2D(S2)/σ4=2(n-1)
D(S2)=2σ4/(n-1)=2σ4/15解析： 暂无解析 -
第12题：
问答题设总体X～N(μ,σ2)，x1,x2,…xn为其样本，为样本均值,则____．正确答案：解析： -
第13题：
设X～N(80，202)，
为样本容量n＝100的样本均值，则P(|-80|≥3)为( )。A．2Φ(1.5)-1
B．1-2Φ(3)
C．2-2Φ(1.5)
D．2-2Φ(3)
正确答案：C
解析：P(|-80|3)＝2Φ(1.5)-1；P(|-80|3)＝1-P(|-80|3＝＝2-2Φ(1.5) -
第14题：
设X～N(μ，σ2)，σ未知，xi为样本(i=1，2，…，n)。H0:μ≤μ0，H1:μ＞μ0，α为显著性水平，则接受域( )。
正确答案：C
解析：对单侧要求的假设检验，σ未知，采用t检验，检验统计量，拒绝域为，所以接受域为。 -
第15题：
设X～N(1，4)，
为样本容量n=16的样本均值，则P(0＜≤2)为( )。A．2Ф(0.5)-1
B．2Ф(2)-1
C．1-2Ф(0.5)
D．1-2Ф(2)
正确答案：B
解析：对于X～N(1，4)分布，知～N(1，0.52)，可转化为U=(-1)/0.5～N(0，1)，则可得P(0≤2)=Ф[(2-1)/0.5]-Ф(-1/0.5)=2Ф(2)-1。 -
第16题：
设总体X～N（μ,σ^2）,其中σ^2未知,^2s=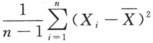
,样本容量n,则参数μ的置信度为1－a的置信区间为().
答案：D解析：因为σ^2未知，所以选用统计量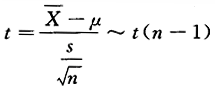
，故μ的置信度为1-α的置信区间为
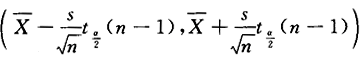，选(D). -
第17题：
设随机变量X~N(0，σ2)，则对于任何实数λ，都有：
A. P(X≤λ)=P(X≥λ)
B.P(X≥λ)=P(X≤-λ)
C.X-λ~N(λ,σ2-λ2)
D.λX~N(0,λσ2)答案：B解析：
Y=aX+b~N(au+b,a2σ2)，或利用u=0时概率密度f(x)曲线的对称性，概率(积分值)与曲边梯形面积对应判断。 -
第18题：
设 X、Y相互独立，X~N(4，1),Y~N(1，4),Z=2X-Y，则
A.0 B.8 C. 15 D. 16答案：B解析：提示：由方差性质D(Z) =D(2X)+D(Y) = 4D(X)+D(Y) = 4x1 + 4。 -
第19题：
设X~N(1，4),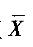
为样本容量n = 16的样本均值，则P(0≤2)为（ ）。
A. 2Φ(0.5)-1 B. 2Φ(2) -1 C. 1-2Φ(0.5) D. 1 -2Φ(2)答案：B解析：对于X~N(1，4)分布，知
~N(1, 0.52)，可转化为U= (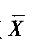
-1)/0.5 ~N(0， 1)，则可得P(0≤2)=Φ[(2-1)/0.5] -Φ(-1/0.5) =2Φ(2) -1。 -
第20题：
正态分布计算所依据的重要性质为（ ）。
A.设X~N(μ,σ2),则μ= (X-μ)/σ~N(0, 1)
B.设X~N(μ,σ2),则对任意实数a、b有P(XC.设X~N(μ,σ2),则对任意实数a、b有P(X>a) =1-Φ[(a-μ)/σ]
D.设X~N(μ,σ2),则对任意实数a、b有P(a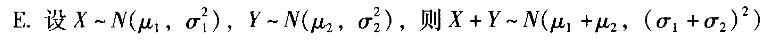
答案：A,B,C,D解析：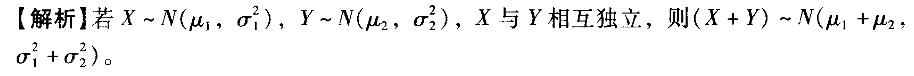
-
第21题：
设总体X～N(u，σ2），基于来自总体X的容量为16的简单随机样本，测得样本均值x= 31.645，样本方差S2=0.09，则总体均值μ的置信度为0.98的置信区间为( )。
A.(30.88, 32.63)
B.(31.45, 31.84)
C.(31.62, 31.97)
D.(30.45, 31.74)答案：B解析：
-
第22题：
问答题设总体X～N(72，100)，为使样本均值大于70的概率不小于90%，则样本容量n至少应取多少?正确答案：解析： -
第23题：
单选题设X～N（1，4），则P（0≤X＜2）可表示为（ ）。A2Φ（0.5）-1
B1-2Φ（0.5）
C2u0.5-1
D1-2u0.5
正确答案： A解析：
由于X～N（1，4）正态分布，则U=（X-1）/2～N（0，1），所以：
P（0≤X＜2）=Φ[（2-1）/2]-Φ（0-1/2）=Φ（0.5）-Φ（-0.5）
=Φ（0.5）-[1-Φ（0.5）]
=2Φ（0.5）-1